跳转到内容

阿基米德

编辑链接
本页使用了标题或全文手工转换
维基百科，自由的百科全书
关于与“阿基米德”标题相近或相同的条目，请见“阿基米德 (消歧义)”。
锡拉库扎的阿基米德
Ἀρχιμήδης
《沉思的阿基米德》（1620年费地（英语：Domenico Fetti）画作）
《沉思的阿基米德》（1620年费地（英语：Domenico Fetti）画作）
出生约前287 年
锡拉库扎
大希腊
逝世约前212 年 （大约75岁）
锡拉库扎
大希腊
知名于
科学生涯
研究领域

阿基米德（希腊语：´Αρχιμήδης；前287年—前212年），希腊化时代的数学家、物理学家、发明家、工程师、天文学家[2]。出生于西西里岛的锡拉库扎，据说他在亚历山大求学时期，发明了阿基米德式螺旋抽水机，今天的埃及仍在使用。第二次布匿战争时，罗马大军围攻锡拉库扎，阿基米德死于罗马士兵之手。

阿基米德对数学和物理学的影响极为深远，被视为古希腊最杰出的科学家[3][4]。美国数学史学家埃里克·坦普尔·贝尔在其《数学大师》一书中将阿基米德与牛顿和高斯并列为有史以来最伟大的三位数学家[5]。

传记

[编辑]

阿基米德于约前287年出生于意大利南部海岸的港口城市锡拉库扎，当时是大希腊的自治殖民地。其生日是根据拜占庭希腊裔历史学家约翰·策策斯（英语：John Tzetzes）的阿基米德活了75岁的说法推算的。[6] 依照阿基米德的《数沙子（英语：The Sand Reckoner）》，阿基米德之父名为菲迪亚斯（希腊文：Φειδίας，Pheidias），是一个天文学家，除此之外我们对其一无所知。普鲁塔克于《名人传》中写道，阿基米德与锡拉库扎的统治者希伦二世有血缘关系。[7]其友赫拉克利特（Heracleides）为阿基米德撰写的传记已经失传，使他生活点滴成为谜团。[8] 我们无从得知他是否结婚，或育有后代。他在年轻时可能曾在古埃及亚历山大学习，科农和埃拉托斯特尼是他的同辈。他把科农称作是他的朋友，他在另两本著作《机械理论方法（英语：Archimedes' use of infinitesimals）》和《奶牛问题（英语：Archimedes' cattle problem）》之引言里提到了埃拉托斯特尼。[a]

《阿基米德之死》 （1815年，Thomas Degeorge（英语：Thomas Degeorge）画作）[9]

约公元前212年，阿基米德死于第二次布匿战争中，当时马克卢斯将军领导的罗马军队在历时两年攻城战后占领了锡拉库扎城。根据来自普鲁塔克的知名说法：当城市被占领时，阿基米德还在思考一个数学画图（英语：mathematical diagram）问题。一名罗马士兵要求他去面见马克卢斯将军。他拒绝了，说要完成这个难题。士兵愤怒难当，挥剑杀死了阿基米德。关于阿基米德之死，普鲁塔克的一个不太出名说法认为他在尝试向罗马士兵投降的时候死亡。按照这个故事，阿基米德当时携带着数学仪器，士兵以为是什么贵重物件，因而杀了他。依记载，马克卢斯将军对阿基米德之死感到很生气，他认为阿基米德是重要的科学家并下令不得伤害他。[10]马克卢斯曾称阿基米德为“几何学的巨人”。[11]

相传阿基米德的遗言是“别打扰我的圆圈”，指当时他被罗马士兵打扰时正在研究的数学画图法中的圆圈。在拉丁语中常作“Noli turbare circulos meos”，但没有确凿证据表明阿基米德确实说了这些话，这在普鲁塔克的说法中也没有出现。公元1世纪，瓦莱里乌斯·马克西姆斯在《难忘的事迹名言》（英：Memorable Doings and Sayings）中记载为：“...sed protecto manibus puluere 'noli' inquit, 'obsecro, istum disturbare'”（“……以双手保护着沙尘，说：‘求你了，别打扰它！’”）。这句话对应的纯正希腊语版本是"μὴ μου τοὺς κύκλους τάραττε!" （拉丁文转写：Mē mou tous kuklous taratte!）。[10]

Cicero Discovering the Tomb of Archimedes （1805年，本杰明·韦斯特画作）

阿基米德之墓上刻着其最喜爱的数学证明的雕塑，包括高度、直径相同的球面和圆柱体。他曾证明球表面积等于其外切圆柱体侧面表面积，球的体积是外切圆柱体体积的2/3。公元前75年，阿基米德死后137年，罗马演说家西塞罗在西西里担任财务官。他听说了阿基米德之墓的故事，但当地没有人能告诉他其之具体位置。最终，他在锡拉库扎的阿格里真托之门附近寻到其墓，无人照料，灌木丛生。西塞罗打扫了其墓，得以阅览其上镌刻的碑文和雕刻。[12] 1960年前期，锡拉库扎当地丽景酒店曾发现一座坟墓，据称属于阿基米德，但没有任何证据可以表明这一点。如今，无人知晓其墓地的具体位置。[13]

“阿基米德传”的标准版本，在他死后许久才由古罗马历史学家写就。锡拉库扎攻城由波利比乌斯在记于其《通史》（英文：“Universal History”）中，大约在阿基米德死后70年写就，此后被普鲁塔克和蒂托·李维引用。此文主要着墨与其为保卫城市所建的“战争机器”，未有详述阿基米德为人。[14]

生平

[编辑]

亚历山大里亚求学

[编辑]

公元前287年，阿基米德出生在西西里岛东南端的锡拉库扎城。阿基米德的父亲是天文学家和数学家，所以他从小受家庭影响，十分喜爱数学。在当时古希腊的辉煌文化已经逐渐衰退，经济、文化中心逐渐转移到托勒密王朝的亚历山大城，大概在他九岁时，父亲送他到埃及的亚历山大城念书，亚历山大城是当时西方世界的知识、文化中心，学者云集，举凡文学、数学、天文学、医学的研究都很发达，阿基米德在这里随许多著名的数学家学习，包括有名的几何学大师欧几里得。

回到锡拉库扎

[编辑]

在经过许多年的求学历程后，阿基米德回到故乡锡拉库扎。据说锡拉库扎的国王希伦二世与阿基米德的父亲是朋友，一说国王与他们是亲戚关系。总之，阿基米德受到国王的礼遇，经常出入宫廷，并常与国王、大臣们畅谈国事或闲话家常。阿基米德在这种优裕的环境下，作了几十年的研究工作，并在数学、力学、机械方面取得了许多重要的发现与成就，成为上古时代欧洲最有创建的科学家。

据说阿基米德经常为了研究而废寝忘食，走进他的住处，随处可见数字和方程式，地上则是画满了各式各样的图形，墙上与桌上也无法幸免地成了他的计算板。

布匿战争时期

[编辑]

公元前3世纪末，正是罗马共和国与迦太基，为了争夺西西里岛的霸权而开战的时期。地处西西里岛的锡拉库扎一直都是投靠罗马，但是公元前216年迦太基大败罗马军队，锡拉库扎的新国王希罗尼姆斯（英语：Hieronymus of Syracuse）（希伦二世的孙子），立即见风转舵与迦太基结盟，罗马共和国于是派马克卢斯将军领军从海路和陆路同时进攻锡拉库扎。国难当前，保家卫国的责任感促使阿基米德奋起抗敌，于是他绞尽脑汁，日以继夜的发明各种御敌武器。

当时阿基米德造了巨大的起重机，可以将敌人的战舰吊到半空中，然后重重摔下使战舰在水面上粉碎；他还利用杠杆原理制造出一批投石机，凡是靠近城墙的敌人，都难逃他飞石与标枪的攻击。这些武器弄得罗马军队惊慌失措、人人害怕，连大将军马克卢斯也不得不承认“这是场罗马舰队与阿基米德一人的战争”、“阿基米德简直是神话中的百手巨人”。

阿基米德之死

[编辑]

由于久攻不下，马克卢斯决定改变策略，以围城的持久战来断绝城内粮食，这个妙计使得阿基米德也无可奈何。公元前212年，锡拉库扎城终于被罗马军队攻陷。相传罗马军队进城时，阿基米德还在自家前的地上画图研究几何问题。罗马士兵走近沉思中的阿基米德，要求他立刻前去面见马克卢斯，并踩坏了画在沙地上的图形。阿基米德大骂：“别碰我的图！”士兵一气之下便杀了阿基米德。

成就

[编辑]

数学

[编辑]
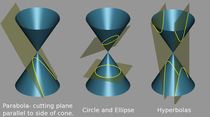
“Stomachion”是阿基米德再生羊皮书（英语：Archimedes Palimpsest）里的一个类似七巧板的拼图，由14块碎片组成的几何拼图问题。

对于阿基米德来说，工程机械和物理上的发明只是次要的，他更感兴趣而且投注更多时间的是纯理论上的研究，尤其是在数学和天文学方面。在数学方面，他利用“逼近法”算出球表面积、球体积、抛物线、椭圆面积，后世的数学家依据这种方法加以发展成近代的“微积分”。他还研究出螺旋形曲线的性质，现今的“阿基米德螺线”曲线，就是为纪念他而命名。另外他在《数沙者》一书中，他创造了一套记录庞大数目的方法，简化了记数的方式。

经由研究阿基米德再生羊皮书（英语：Archimedes Palimpsest）上的文字，科学家发现了失传的阿基米德手稿，并加以解读。在残卷《方法》命题14中，阿基米德提出无穷大的概念，是现代集合论的基础。在残卷《Stomachion》（中文译名为“阿基米德小房[15]”，英文译名直译为“阿基米德盒子”）中，由教士约翰·麦隆纳斯于公元1229 年4 月14 日抄写，想在耶稣复活周年日，当作礼物献给教会，阿基米德经由一种类似七巧板的图形游戏，研究以十四片碎片组成正方形的所有拼法（一共17152种方法，并可分成536个大类），成为组合学最早的开端。

圆周率
3.1415926535897932384626433...
运用
证明
值
人物
历史
文化
相关主题

当阿基米德经常被视为一个机械装置的工程师时，他也做了有关于数学领域的贡献。普鲁塔克写道：“他将他全部的情感和野心完全的投注在那些单纯的猜测里头，而在那里可能不需要有庸俗的生活。”

阿基米德使用无穷小量的数学分析方式，类似现在的微积分。通过反证法，他甚至可以让问题的答案达到任意精确度，同时也给出答案所在的范围。这种技术被称为穷举法，并且他使用这种方法计算出了圆周率的近似值。他做出圆的外接多边型和内接多边型。随着多边形的边数增加，将会越来越接近圆。

阿基米德将欧几里得提出的趋近观念作了有效的运用，他提出圆内接多边形和相似圆外切多边形，当边数足够大时，两多边形的周长便一个由上，一个由下的趋近于圆周长。他先用六边形，以后逐次加倍边数，到了九十六边形，阿基米德计算出其面积，并且指出圆周率的值: <Π < ；:也就是 [16]

他还证明了圆面积等于圆周率乘以半径的平方。在球体和圆柱的研究中，阿基米德假设，一个任意的数在自加足够多的次数之后，会大于任意一个给定的数。这被称为实数的阿基米德性质。另外他算出球的表面积是其内接最大圆面积的四倍。而他导出圆柱内切球体的体积是圆柱体积的三分之二，这个定理就刻在他的墓碑上。

在其著作《圆的测量》中，阿基米德给出了3的平方根的近似值，介于265 ⁄ 153 (约为1.7320261)和1351 ⁄ 780 (约为1.7320512)之间。其实际值大约为1.7320508，这是一个非常准确的近似值。他直接给出了结果却没有给出任何计算方法的解释。由此，约翰·沃利斯作出如下评价：“这就像是故意的，似乎阿基米德已经决定不向后人们透露他的算法的秘密，只是强迫他们接受他的结果。”

几何学

[编辑]

阿基米德是第一位讲科学的工程师，在他的研究中，使用欧几里得的方法，先假设，再得到结果，他不断地寻求一般性的原则用于特殊的工程上。他的作品始终融合数学和物理，因此阿基米德成为物理学之父。

他应用杠杆原理于战争，保卫西拉斯鸠的事迹是家喻户晓的。而他也以同一原理导出部分球体的体积、回转体的体积（椭球、回转抛物面、回转双曲面），此外，他也讨论阿基米德螺线（例如：苍蝇由等速旋转的唱盘中心向外走去所留下的轨迹），圆、球体、圆柱的相关原理，成就斐然。

天文学

[编辑]

在天文学方面，阿基米德曾运用水力制作一座天象仪，球面上有日、月、星辰和五大行星，根据记载，这个天象仪不但运行精确，连何时会发生月食、日食都能加以预测。晚年的阿基米德开始怀疑地球中心学说(地心说)，并猜想地球有可能绕太阳转动，这个观念一直到哥白尼时代才被人们提出来讨论。

其他

[编辑]
手持圆规研究图形的阿基米德。

虽然杠杆原理不是阿基米德发现的，但是他在他的卫面平衡研究中解释了其工作原理。以亚里士多德的追随者为主的逍遥学派学校中曾出现过更早的关于杠杆的描述，也有说是阿尔库塔斯。根据帕普斯所述，阿基米德关于杠杆的研究曾引出过其非常著名的一句话：“给我一个支点，我可以举起整个地球。”普鲁塔克曾描述过阿基米德是如何设计滑轮机构的，该机构可以让水手们利用杠杆原理提起那些过重的无法单凭人力搬运的物品。阿基米德也被认为曾改进过投射器的威力和准确度，并且发明了在第一次布匿战争中使用的计程器。这个计程器是一种车辆的形式，在每行驶过一定距离后车上的齿轮机构就会向特定容器中投入一个球。

西塞罗在他的对话录《国家论》中曾大致提到过阿基米德，这部对话录描述了一段发生在公元前129年的虚构的谈话。公元前212年，据说在占领锡拉库扎之后，马库斯·克劳狄斯·马塞勒斯将军将两部用于天文学的机械装置带回了罗马，这两部装置显示了太阳，月亮和五个行星的运动。西塞罗还提到了由泰勒斯和欧多克索斯设计的类似装置。对话录表明，马塞勒斯将其中一部机器据为已有，另外一部则捐赠给了罗马的功德庙。马塞勒斯持有的那一部后来被公开展示，据西塞罗说，加勒斯向斐勒斯（英语：Lucius Furius Philus）演示的过程被后者记录如下

这是一段关于天象仪或是太阳系仪的描述。帕普斯曾说过，阿基米德有一些手稿（现已丢失）被命名为“球体制造”，其中有关于此类机械装置的制造方法。在这方面的现代研究主要集中在安提基特拉机械上，这是另外一个可能出于相同目的而设计的古代机械。制造这类机械需要极其尖端的差动齿轮知识和技术。这曾一度被认为已经超出了古代的技术能力范畴，但1902年发现的安提基特拉机械可以证明早在古希腊这类装置就已经出现了。

著作

[编辑]

轶事

[编辑]

真假皇冠

[编辑]
主条目：阿基米德浮体原理
阿基米德可能使用了浮力的原理来判断黄金王冠的密度是否小于等同质量的纯金块。

希伦二世国王，请金匠用纯金打造了一顶纯金王冠，做好了以后，吹哨者密报金匠造假掺了“白银”在里面，但是又不能把王冠毁坏来鉴定。阿基米德想了好久，一直没有好方法，吃不下饭也睡不好觉。有一天，他在洗澡的时候发现，当他坐在浴盆里时水位上升了，这使得他想到了：“上升了的水位正好应该等于王冠的体积，所以只要拿与王冠等重量的金子，放到水里，测出它的体积，看看它的体积是否与王冠的体积相同，如果王冠体积更大，这就表示其中造了假，掺了银。”

阿基米德想到这里，不禁高兴的从浴盆跳了出来，赤身裸体跑了出去，边跑还边喊着：“尤里卡，尤里卡！”（希腊语:εύρηκα，意即“发现了！”）然经过证明之后，王冠中确实含有白银，阿基米德成功的揭穿了金匠的舞弊诡计，国王对他当然是更加的信服了。

后来阿基米德将这个发现进一步总结出浮力理论，为浮体学建立了基本的定理，并写在他的《浮体论》著作里，也就是：物体在流体中所受的浮力，等于物体所排开的流体的重量。

举起地球

[编辑]
阿基米德说过：“给我一个支点和杠杆，我可以铲起整个地球。”

阿基米德对于机械的研究源自于他在亚历山大城求学时期。有一天阿基米德在久旱的尼罗河边散步，看到农民提水浇地相当费力，经过思考之后他发明了一种利用螺旋作用在水管里旋转而把水吸上来的工具，后世的人叫它做“阿基米德螺旋提水器”，埃及一直到二千年后的现在，还有人使用这种器械。这个工具成了后来螺旋推进器的先祖。

当时的欧洲，在工程和日常生活中，经常使用一些简单机械，譬如螺丝、滑车、杠杆、齿轮等，阿基米德花了许多时间去研究，发现了“杠杆原理”和“力矩”的观念，对于经常使用工具制作机械的阿基米德而言，将理论运用到实际的生活上是轻而易举的。他曾说只要给他一个支点和棒子，他就可以举起整个地球（当然这只是比喻，因为太空没有重力）。

刚好此时国王希伦二世遇到了一个棘手的问题：他替埃及托勒密王造了一艘船，但因为船太大太重，无法放进海里，国王就对阿基米德说：“你连地球都举得起来，把一艘船放进海里应该很容易吧？”于是阿基米德迅速地巧妙组合各种机械，造出一架机具。在一切准备妥当后，将牵引机的绳子交给国王，国王轻轻一拉，大船果然移动下水，国王不得不为阿基米德的天才所折服。从这个历史故事我们可以知道，阿基米德可能是当时全世界对于机械的原理与运用，了解最透彻的人。

参见

[编辑]

注释

[编辑]

a. ^ In the preface to On Spirals addressed to Dositheus of Pelusium, Archimedes says that "many years have elapsed since Conon's death." Conon of Samos lived c. 280–220 BC, suggesting that Archimedes may have been an older man when writing some of his works.

b. ^ The treatises by Archimedes known to exist only through references in the works of other authors are: On Sphere-Making and a work on polyhedra mentioned by Pappus of Alexandria; Catoptrica, a work on optics mentioned by Theon of Alexandria; Principles, addressed to Zeuxippus and explaining the number system used in The Sand Reckoner; On Balances and Levers; On Centers of Gravity; On the Calendar. Of the surviving works by Archimedes, T. L. Heath offers the following suggestion as to the order in which they were written: On the Equilibrium of Planes I, The Quadrature of the Parabola, On the Equilibrium of Planes II, On the Sphere and the Cylinder I, II, On Spirals, On Conoids and Spheroids, On Floating Bodies I, II, On the Measurement of a Circle, The Sand Reckoner.

c. ^ Boyer, Carl Benjamin A History of Mathematics (1991) ISBN 0-471-54397-7 "Arabic scholars inform us that the familiar area formula for a triangle in terms of its three sides, usually known as Heron's formula — k = √s(s − a)(s − b)(s − c), where s is the semiperimeter — was known to Archimedes several centuries before Heron lived. Arabic scholars also attribute to Archimedes the 'theorem on the broken chord' ... Archimedes is reported by the Arabs to have given several proofs of the theorem."

d. ^ "It was usual to smear the seams or even the whole hull with pitch or with pitch and wax". In Νεκρικοὶ Διάλογοι (Dialogues of the Dead), Lucian refers to coating the seams of a skiff with wax, a reference to pitch (tar) or wax.[17]

参考文献

[编辑]
  1. ^ Knorr, Wilbur R. Archimedes and the spirals: The heuristic background. Historia Mathematica（英语：Historia Mathematica） (爱思唯尔). 1978, 5 (1): 43–75. "To be sure, Pappus does twice mention the theorem on the tangent to the spiral [IV, 36, 54]. But in both instances the issue is Archimedes' inappropriate use of a "solid neusis," that is, of a construction involving the sections of solids, in the solution of a plane problem. Yet Pappus' own resolution of the difficulty [IV, 54] is by his own classification a "solid" method, as it makes use of conic sections." (page 48) 
  2. ^ Archimedes (c.287 - c.212 BC). BBC History. [2012-06-07]. （原始内容存档于2018-10-04）. 
  3. ^ Calinger, Ronald. A Contextual History of Mathematics. Prentice-Hall. 1999: 150. ISBN 0-02-318285-7. Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity. 
  4. ^ Archimedes of Syracuse. The MacTutor History of Mathematics archive. 1999年1月 [2008-06-09]. （原始内容存档于2013-06-20）. 
  5. ^ Bell, Eric Temple. Men of mathematics 1st Touchstone. Simon & Schuster. 1986-10-15. ISBN 9780671628185. 
  6. ^ Heath, T. L.（英语：T. L. Heath）, Works of Archimedes, 1897
  7. ^ 普鲁塔克. Parallel Lives Complete e-text from Gutenberg.org. 古腾堡计划. [2007-07-23]. （原始内容存档于2007-07-11）. 
  8. ^ O'Connor, J.J.; Robertson, E.F. Archimedes of Syracuse. University of St Andrews. [2007-01-02]. （原始内容存档于2007-02-06）. 
  9. ^ The Death of Archimedes: Illustrations. math.nyu.edu. New York University. [2018-11-17]. （原始内容存档于2015-09-29）. 
  10. ^ 10.0 10.1 Rorres, Chris. Death of Archimedes: Sources. Courant Institute of Mathematical Sciences. [2007-01-02]. （原始内容存档于2006-12-10）. 
  11. ^ Mary Jaeger. Archimedes and the Roman Imagination, p. 113.
  12. ^ Rorres, Chris. Tomb of Archimedes: Sources. Courant Institute of Mathematical Sciences. [2007-01-02]. （原始内容存档于2006-12-09）. 
  13. ^ Rorres, Chris. Tomb of Archimedes – Illustrations. Courant Institute of Mathematical Sciences. [2011-03-15]. （原始内容存档于2019-05-02）. 
  14. ^ Rorres, Chris. Siege of Syracuse. Courant Institute of Mathematical Sciences. [2007-07-23]. （原始内容存档于9 June 2007）. 
  15. ^ 希思, T.L. 《阿基米德全集（修订版）》. 陕西科学技术出版社. 2010年12月. ISBN 978-7-5369-2342-3. 
  16. ^ 阿基米德原著 《量圆》 《中国数学史大系》 副卷第一 第二章 第三编 希腊 197-203页
  17. ^ Casson, Lionel. Ships and seamanship in the ancient world. Baltimore: The Johns Hopkins University Press. 1995: 211–212 [2018-11-17]. ISBN 978-0-8018-5130-8. （原始内容存档于2021-04-17）. 

延伸阅读

[编辑]
英文维基文库中的《1911年版大英百科全书》条目：Archimedes

http://www.wilbourhall.org （页面存档备份，存于互联网档案馆） 《阿基米德著作》Heiberg版的PDF扫描件，现属公共领域]

外部链接

[编辑]
检索自“https://zh.wikipedia.org/w/index.php?title=阿基米德&oldid=84254159”