中線定理,又稱阿波羅尼奧斯定理,是歐氏幾何的定理,表述三角形兩邊和中線長度關係。它等價於平行四邊形恆等式。
對任意三角形 ,設
,設 是線段
是線段 的中點,
的中點, 為中線,則有如下關係:
為中線,則有如下關係:

用萊布尼茨標量函數約簡,可以容易導出這性質:只需要在兩個平方中引入 :
:

得出

 是
是 的中點,因此
的中點,因此 和
和 相反,可知式中兩個標積抵消。又因
相反,可知式中兩個標積抵消。又因 ,得出
,得出


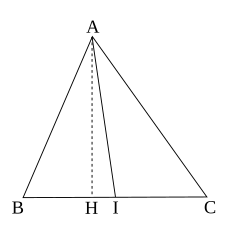
這可能是阿波罗尼奥斯的證明方法,因為他不知道萊布尼茨函數。證明如下:
設 是從
是從 到
到 的垂足,則
的垂足,則 和
和 是直角三角形。用勾股定理可得
是直角三角形。用勾股定理可得



所以

把 和
和 用
用 和
和 表達出來(記得
表達出來(記得 是
是 的中點,因此
的中點,因此 )。注意到雖然現在的情形假設
)。注意到雖然現在的情形假設 在線段
在線段 上,但其
他情形也可以用這個方法。
上,但其
他情形也可以用這個方法。


代入前式:



 是直角三角形(H為
是直角三角形(H為 於
於 之垂足)
,因此
之垂足)
,因此

代入前式得出

設 是線段
是線段 的中點,則有
的中點,則有
用標積表示 ,其中
,其中 是
是 到線
到線 的垂足。
的垂足。
從上得到中線的另一條定理 。
。
實際上

 投影在
投影在 上是
上是 ,因而有
,因而有 .
.
這兩個共線向量的標積可等於 或其負數,因此取絕對值。
或其負數,因此取絕對值。











































