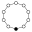
小群列表
外觀
這個列表可以被用來決定一個給定的有限群G會同構於哪一種群:首先確定G的階,然後再找下面列表中有相同階的候選群。若知道G為可換與否,某些的候選群便可以立刻被刪掉。為了分別剩下的候選群,可以看給定之群內每個元素的階,並對照候選群內每個元素的階。
術語
[編輯]- Zn:其階為n之循環群(通常Cn或Z/nZ之符號也會被使用)。
- Dihn:其階為2n的二面體群(通常Dn之符號也會被使用,有時則會用D2n)。
- Sn:n階的對稱群,包含有n!個n個元素的置換。
- An:n階的交錯群,包含有n!/2個n個元素的偶置換。
- Dicn:其階為4n的雙循環群。
Zn和Dihn之符號在三維點群Cn和Dn中有著沒有相同符號的優點。其存在著多於此兩類的等距同構群,但這些都有著相同的抽象群類型。
符號G × H表示是兩個群的直積。阿貝爾群和簡單群會加上注釋(對小於60階之群,簡單群會恰好是循環群Zn,其中的n為質數。)下面會以等號(=)來標註同構。
環圖內的單位元素會以黑圓圈來表示。圖環不能唯一地表示一個群之最小階為16。
下面列表中的子群,當然群和群自身並不會被列出來。
小非可換群的列表
[編輯]另見小阿貝爾群列表和下面合併的列表。
注意如「3×Z2」之標記表示其有3個Z2類型的子群(而不是Z2的一個左陪集),而其他地方裡的×則表示直積。
| 階 | 群 | 子群 | 性質 | 環圖 |
|---|---|---|---|---|
| 6 | S3 = Dih3 | Z3 , 3 × Z2 | 最小的非可換群 | |
| 8 | Dih4 | Z4, 2 × Dih2 , 5 × Z2 | 非可換 | |
| 四元群, Q8 = Dic2 | 3 × Z4 , Z2 | 非可換;最小的漢彌爾頓群 | ||
| 10 | Dih5 | Z5 , 5 × Z2 | 非可換 | |
| 12 | Dih6 = Dih3 × Z2 | Z6 , 2 × Dih3 , 3 × Dih2 , Z3 , 7 × Z2 | 非可換 |  |
| A4 | Z22, 4 × Z3, 3 × Z2 | 非可換;最小確定拉格朗日定理之相反敘述不是對的群:沒有6階的子群 |  |
|
| Dic3 = Z3和Z4的半直積,其中Z4以反演作用於Z3上 | Z2, Z3, 3 × Z4, Z6 | 非可換 |  |
|
| 14 | Dih7 | Z7 , 7 × Z2 | 非可換 |  |
| 16 | Dih8 | Z8 , 2 × Dih4 , 4 × Dih2 , Z4 , 9 × Z2 | 非可換 |  |
| Dih4 × Z2 | 2 × Dih4 , Z4 × Z2 , 2 × Z23, 7 × Z22 , 2 × Z4 , 11 × Z2 | 非可換 |  |
|
| 廣義四元群, Q16 = Dic4 | 非可換 |  |
||
| Q8 × Z2 | 非可換、漢彌爾頓群 | 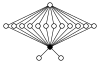 |
||
| 16階之擬二面體群 | 非可換 | 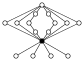 |
||
| 16階之模群 | 非可換 |  |
||
| Z4和Z4的半直和,其中一個以反演作用在另一個上 | 非可換 |  |
||
| 由泡利矩陣產生的群 | 非可換 |  |
||
| G4,4 | 非可換 |  |
合併列表
[編輯]| 階 | 群 | 子群 | 性質 | 環圖 |
|---|---|---|---|---|
| 1 | 平凡群 = Z1 = S1 = A2 | - | 平凡、循環、交錯、對稱、初等 | |
| 2 | Z2 = S2 = Dih1 | - | 可換、簡單、最小非當然群 | |
| 3 | Z3 = A3 | - | 可換、簡單 | |
| 4 | Z4 | Z2 | 可換 | |
| 克萊因四元群 = Z2 × Z2 = Dih2 | 3 × Z2 | 可換、最小非循環群 | ||
| 5 | Z5 | - | 可換、簡單 | |
| 6 | Z6 = Z2 × Z3 | Z2 , Z3 | 可換 | |
| S3 = Dih3 | Z3 , 3 × Z2 | 最小非可換群 | ||
| 7 | Z7 | - | 可換、簡單 | |
| 8 | Z8 | Z4 , Z2 | 可換 | |
| Z2 ×Z4 | 2 × Z4 , 3 ×Z2 , Dih2 | 可換 | ||
| Z2 × Z2 × Z2 = Dih2 × Z2 | 7 × Z2 × Z2 , 7 × Z2 | 可換 | ||
| Dih4 | Z4, 2 × Dih2 , 5 × Z2 | 非可換 | ||
| 四元群, Q8 = Dic2 | 3 × Z4 , Z2 | 非可換、最小漢彌爾頓群 | ||
| 9 | Z9 | Z3 | 可換 | |
| Z3 × Z3 | 4 × Z3 | 可換 | ||
| 10 | Z10 = Z2 × Z5 | Z5 , Z2 | 可換 | |
| Dih5 | Z5 , 5 × Z2 | 非可換 | ||
| 11 | Z11 | - | 可換、簡單 | |
| 12 | Z12 = Z4 × Z3 | Z6 , Z4 , Z3 , Z2 | 可換 |  |
| Z2 × Z6 = Z2 × Z2 × Z3 = Dih2 × Z3 | 3 × Z6, Z3, Dih2, 3 × Z2 | 可換 |  |
|
| Dih6 = Dih3 × Z2 | Z6 , 2 × Dih3 , 3 × Dih2 , Z3 , 7 × Z2 | 非可換 |  |
|
| A4 | Z22, 4 × Z3, 3 × Z2 | 非可換;最小確定拉格朗日定理之相反敘述不是對的群:沒有6階的子群 |  |
|
| Dic3 = Z3和Z4的半直積,其中Z4以反演作用於Z3上 | Z2, Z3, 3 × Z4, Z6 | 非可換 |  |
|
| 13 | Z13 | - | 可換、簡單 | 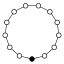 |
| 14 | Z14 = Z2 × Z7 | Z7 , Z2 | 可換 | 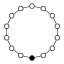 |
| Dih7 | Z7 , 7 × Z2 | 非可換 |  |
|
| 15 | Z15 = Z3 × Z5 | Z5 , Z3 | 可換 | 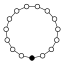 |
| 16 | Z16 | Z8 , Z4 , Z2 | 可換 |  |
| Z24 | 15 × Z2, 35 × Dih2, 15 × Z23 | 可換 |  |
|
| Z4 × Z22 | 7 × Z2, 4 × Z4, 7 × Dih2, Z23, 6 × Z4 × Z2 | 可換 |  |
|
| Z8 × Z2 | 3 × Z2, 2 × Z4, Dih2, 2 × Z8, Z4 × Z2 | 可換 |  |
|
| Z42 | 3 × Z2, 6 × Z4, Dih2, 3 × Z4 × Z2 | 可換 |  |
|
| Dih8 | Z8 , 2 × Dih4 , 4 × Dih2 , Z4 , 9 × Z2 | 非可換 |  |
|
| Dih4 × Z2 | 2 × Dih4 , Z4 × Z2 , 2 × Z23, 7 × Z22 , 2 × Z4 , 11 × Z2 | 非可換 |  |
|
| 廣義四元群, Q16 = Dic4 | 非可換 |  |
||
| Q8 × Z2 | 非可換、漢彌爾頓群 |  |
||
| 16階之擬二面體群 | 非可換 |  |
||
| 16階之模群 | 非可換 |  |
||
| Z4和Z4的半直和,其中一個以反演作用在另一個上 | 非可換 |  |
||
| 由泡利矩陣產生的群 | 非可換 |  |
||
| G4,4 | 非可換 |  |
小群圖書館
[編輯]群論電腦代數系統GAP包含著描述了「小」階之群的「小群圖書館」。這些群以同構為分列出。現在,這個圖書館已包含了下列個群:
- 至多2000階的群,除了1024階的(423 164 062個群);
- 55階和74階的群(92個群);
- qn×p階的群,其中qn整除28、36、55或74且p為不同於q的任意質數;
- 因式分解成至多3個質數的群。
它包含著上述的群以電腦上可讀形式顯示之詳盡描述。
這個圖書館由Hans Ulrich Besche、Bettina Eick和Eamonn O'Brien所建構及準備;見http://www.tu-bs.de/~hubesche/small.html。[永久失效連結]