inversion numbers (OEIS 數列A034968 ), which have the same parity as the permutation.在数学 中,当X 是一个至少有两个元素的有限集合 时,X 的置换 (即从X 到X 的双射 )可分为大小相同的两类:奇置换 与偶置换 。如果X 固定了任何一个全序 ,X 的一个置换
σ
{\displaystyle \sigma }
可以定义为
σ
{\displaystyle \sigma }
X 中二元组
x
,
y
{\displaystyle x,y}
x
<
y
{\displaystyle x<y}
σ
(
x
)
>
σ
(
y
)
{\displaystyle \sigma (x)>\sigma (y)}
σ
(
x
)
{\displaystyle \sigma (x)}
σ
{\displaystyle \sigma }
x
{\displaystyle x}
一个置换
σ
{\displaystyle \sigma }
符号 (sign或signature )记作sgn(σ) :如果
σ
{\displaystyle \sigma }
σ
{\displaystyle \sigma }
对称群 S n 交错特征 。置换的符号另一个更一般的符号为列维-奇维塔符号 (
ϵ
σ
{\displaystyle \epsilon _{\sigma }}
X 到X 的所有映射上,而在非双射映射上取值为0。
置换的符号可以清晰地表达为
sgn
(
σ
)
=
(
−
1
)
N
(
σ
)
{\displaystyle \operatorname {sgn}(\sigma )=(-1)^{N(\sigma )}}
这里
N
(
σ
)
{\displaystyle N(\sigma )}
σ
{\displaystyle \sigma }
σ
{\displaystyle \sigma }
对换 分解定义为
sgn
(
σ
)
=
(
−
1
)
m
{\displaystyle \operatorname {sgn}(\sigma )=(-1)^{m}}
这里m 是分解中对换的个数。尽管这样一个分解不是惟一的,所有分解中对换个数的奇偶性是相同的,蕴含着置换的符号是良定义 的。
考虑集合{1,2,3,4,5}的置换σ,它将初始排列12345变为34521。可以通过三个对换得到:首先交换1和3的位置,然后交换2和4,最后交换1和5。这证明了给定的置换σ是奇的。利用置换 一文中的记号,我们可写成
σ
=
(
1
2
3
4
5
3
4
5
2
1
)
=
(
1
3
5
)
(
2
4
)
=
(
1
5
)
(
2
4
)
(
1
3
)
{\displaystyle \sigma ={\begin{pmatrix}1&2&3&4&5\\3&4&5&2&1\end{pmatrix}}={\begin{pmatrix}1&3&5\end{pmatrix}}{\begin{pmatrix}2&4\end{pmatrix}}={\begin{pmatrix}1&5\end{pmatrix}}{\begin{pmatrix}2&4\end{pmatrix}}{\begin{pmatrix}1&3\end{pmatrix}}}
有无穷种方式将σ写成换位的复合 ,例如
σ
=
(
23
)
(
12
)
(
24
)
(
35
)
(
45
)
,
{\displaystyle \sigma =(23)(12)(24)(35)(45),\;}
但是不可能将其写为偶数个换位的复合。
恒同置换是偶置换。一个偶置换可以由恒同置换通过偶数 次两个元素互换(称为对换 )得到,而一个奇置换可由奇数次对换得到。
由整数加法相应的法则马上得到下列性质:
两个偶置换的复合是偶的
两个奇置换的复合是偶的
一个奇置换与偶置换的复合是奇的 由此得到
考虑集合{1,...,n }的所有置换之对称群 Sn ,我们可总结为映射
sgn
:
S
n
→
{
−
1
,
1
}
{\displaystyle \operatorname {sgn} :S_{n}\to \{-1,1\}}
将每个置换映为其符号是一个群同态 。
进一步,我们见到偶置换组成Sn 的一个子群。这就是n 个字母上的交错群 ,记作An 。它是符号同态的核 。奇置换不能组成一个子群,因为两个奇置换的复合是偶置换,但它们是An (在Sn 中)的一个陪集 。
如果n >1,则Sn 中偶置换与奇置换一样多;从而An 包含n !
一个轮换是偶的当且仅当它的长度是奇的。这得自如下类似公式
(a b c d e ) = (a e ) (b e ) (c e ) (d e ) 特别地,为了确定给定的置换是偶的还是奇的,将它写成不交轮换的乘积。这个置换是奇的当且仅当这个分解包含奇数个偶长度的轮换。
每个奇数阶 置换必须是偶的;反之一般不成立。
任意置换可以由一列对换产生:对第一个对换我们将置换的第一个元素放到它恰当的位置,第二个对换放第二个元素,等等。给定一个置换σ,我们可用无数种方式将其写成对换之积。我们要证明所有这样一个分解,要么都有偶数个对换,要么有奇数个对换。
假设我们有两个这样的分解:
σ = T'1 T'2 ... T'k'
σ = Q'1 Q'2 ... Q'm' 我们要证明k'与m'要么都是偶的,要么都是奇的。
每个对换可以写成奇数个相邻元素的对换之乘积,例如
(2 5) = (2 3)(3 4)(4 5)(4 3)(3 2) 如果我们将上面的T'1...T'k'与Q'1...Q'm'中每个对换作这样的分解,我们得到一个新的分解:
σ = T1 T2 ... Tk
σ = Q1 Q2 ... Qm 这里所有T 1...Tk Q 1...Qk 是相邻对换,k − k '是偶数,m − m '是偶数。
现在将T1的逆与σ复合。T 1是两个相邻数 (i , i + 1)的对换,所以与σ相比,新置换σ(i , i + 1)恰好少一个(若 (i ,i + 1)是σ的反向对)或多一个反向对(若 (i ,i + 1)不是σ的反向对)。然后以相同的方法应用到T 2, T 3, ... Tk 的逆,“消解”了置换σ。最后我们得到了恒同置换,它的N 是零,这意味着首先的N (σ)减去k 是偶数。
对另一个置换Q 1...Qm 我们对同样的事情,从而首先的N (σ)减去m是偶数
这样m − k 是偶数,这就是我们要证明的。
现在我们可以定义置换σ是偶的,如果N (σ)是偶数;是奇的,如果N (σ)是奇数。这与首先给出的定义相同,但现在清晰地看到每个置换不是偶的就是奇的。
另一个证明利用多项式
P
(
x
1
,
…
,
x
n
)
=
∏
i
<
j
(
x
i
−
x
j
)
.
{\displaystyle P(x_{1},\ldots ,x_{n})=\prod _{i<j}(x_{i}-x_{j}).\;}
例如在n = 3的情形,我们有
P
(
x
1
,
x
2
,
x
3
)
=
(
x
1
−
x
2
)
(
x
2
−
x
3
)
(
x
1
−
x
3
)
.
{\displaystyle P(x_{1},x_{2},x_{3})=(x_{1}-x_{2})(x_{2}-x_{3})(x_{1}-x_{3}).\;}
现在对{1,...,n }的一个给定置换σ,我们定义
sgn
(
σ
)
=
P
(
x
σ
(
1
)
,
…
,
x
σ
(
n
)
)
P
(
x
1
,
…
,
x
n
)
{\displaystyle \operatorname {sgn} (\sigma )={\frac {P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}{P(x_{1},\ldots ,x_{n})}}}
因为多项式
P
(
x
σ
(
1
)
,
…
,
x
σ
(
n
)
)
{\displaystyle P(x_{\sigma (1)},\dots ,x_{\sigma (n)})}
P
(
x
1
,
…
,
x
n
)
{\displaystyle P(x_{1},\dots ,x_{n})}
sgn
(
σ
τ
)
=
P
(
x
σ
(
τ
(
1
)
)
,
…
,
x
σ
(
τ
(
n
)
)
)
P
(
x
1
,
…
,
x
n
)
{\displaystyle \operatorname {sgn} (\sigma \tau )={\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{1},\ldots ,x_{n})}}}
=
P
(
x
σ
(
1
)
,
…
,
x
σ
(
n
)
)
P
(
x
1
,
…
,
x
n
)
⋅
P
(
x
σ
(
τ
(
1
)
)
,
…
,
x
σ
(
τ
(
n
)
)
)
P
(
x
σ
(
1
)
,
…
,
x
σ
(
n
)
)
{\displaystyle ={\frac {P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}{P(x_{1},\ldots ,x_{n})}}\cdot {\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}}}
=
sgn
(
σ
)
⋅
sgn
(
τ
)
{\displaystyle =\operatorname {sgn} (\sigma )\cdot \operatorname {sgn} (\tau )}
有此定义之后,显然任何两个相邻元素的对换有符号−1,这样我们事实上重新得到了早先定义的符号。
第三个证明利用群Sn 一个呈示 ,使用生成元为
τ
1
,
…
,
τ
n
−
1
{\displaystyle \tau _{1},\dots ,\tau _{n-1}}
τ
i
2
=
1
{\displaystyle \tau _{i}^{2}=1}
i ,
τ
i
τ
i
+
1
τ
i
=
τ
i
+
1
τ
i
τ
i
+
1
{\displaystyle \tau _{i}\tau _{i+1}\tau _{i}=\tau _{i+1}\tau _{i}\tau _{i+1}}
i < n − 1,
τ
i
τ
j
=
τ
j
τ
i
{\displaystyle \tau _{i}\tau _{j}=\tau _{j}\tau _{i}}
i − j | ≥ 2。这里生成元
τ
i
{\displaystyle \tau _{i}}
i , i + 1)。所有的关系将一个词的长度保持或改变2。从一个偶数长词开始使用这些关系后总得到偶数长词,对奇数长词也类似。从而可以毫无歧义地称Sn 中由偶数长词表示的元素是偶的,由奇数长词表示的元素是奇的。
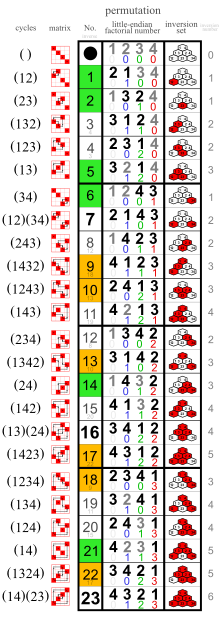
 Permutations of 4 elements
Permutations of 4 elements

























