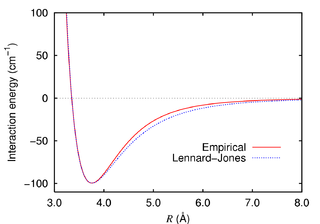
 对应两个氩原子之间作用的兰纳-琼斯势(蓝色),与红色的经验公式值相差很小。
对应两个氩原子之间作用的兰纳-琼斯势(蓝色),与红色的经验公式值相差很小。
兰纳-琼斯势(英语:Lennard-Jones potential),又称L-J势, 6-12势, 或12-6势,是用来模拟两个电中性的分子或原子间相互作用势能的一个比较简单的数学模型。最早由数学家约翰·兰纳-琼斯于1924年提出。由于其解析形式简单而被广泛使用,特别是用来描述惰性气体分子间相互作用尤为精确。
兰纳-琼斯势能以两体距离为唯一变量,包含两个参数。其形式为:
![{\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5256ed833acfbaa9f624a55f4be3f9fcb3c27e1a)
ε等于势能井的深度,σ是互相作用的势能正好为零时的两体距离。在实际应用中,ε、σ参数往往通过拟合已知实验数据或精确量子计算结果而确定。
另一种写法是:
![{\displaystyle V(r)=\epsilon \left[\left({\frac {r_{\text{min}}}{r}}\right)^{12}-2\left({\frac {r_{\text{min}}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c2d6edde2238b5eb6fb9ab277141ef922e351f)
 是在势能井底时两体间距离。
是在势能井底时两体间距离。
从物理意义上讲,第一项 可认为是对应于两体在近距离时以互相排斥为主的作用,第二项
可认为是对应于两体在近距离时以互相排斥为主的作用,第二项 对应两体在远距离以互相吸引(例如通过范德瓦耳斯力)为主的作用,而此六次方项也的确可以使用以电子-原子核的电偶极矩摄动展开得到。但读者尤须记住,兰纳-琼斯势本身只是一个近似公式。
对应两体在远距离以互相吸引(例如通过范德瓦耳斯力)为主的作用,而此六次方项也的确可以使用以电子-原子核的电偶极矩摄动展开得到。但读者尤须记住,兰纳-琼斯势本身只是一个近似公式。
兰纳-琼斯势相应的两体作用力为:

以下是几种常见的兰纳-琼斯势的表示法
此表示法易于模拟软件的使用

其中 ,
, 。或者
。或者![{\displaystyle \sigma ={\sqrt[{6}]{\frac {A}{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c6b59b78a7e87b148cd7731a87362db88f22715) ,
, 。在此表示法中兰纳-琼斯势被写为12-6势。[1]
。在此表示法中兰纳-琼斯势被写为12-6势。[1]
数学上更广义的形式,包含了一个额外的变数n
![{\displaystyle V_{\text{LJ}}(r)=\epsilon \left[\left({\frac {r_{0}}{r}}\right)^{2n}-2\left({\frac {r_{0}}{r}}\right)^{n}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb7a116d65c8b5a0b3aac6ed4949e335c3ac79b)
其中 是分子间的键能(分离原子所需的能量)。
是分子间的键能(分离原子所需的能量)。


![{\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5256ed833acfbaa9f624a55f4be3f9fcb3c27e1a)
![{\displaystyle V(r)=\epsilon \left[\left({\frac {r_{\text{min}}}{r}}\right)^{12}-2\left({\frac {r_{\text{min}}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c2d6edde2238b5eb6fb9ab277141ef922e351f)







![{\displaystyle \sigma ={\sqrt[{6}]{\frac {A}{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c6b59b78a7e87b148cd7731a87362db88f22715)

![{\displaystyle V_{\text{LJ}}(r)=\epsilon \left[\left({\frac {r_{0}}{r}}\right)^{2n}-2\left({\frac {r_{0}}{r}}\right)^{n}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb7a116d65c8b5a0b3aac6ed4949e335c3ac79b)
