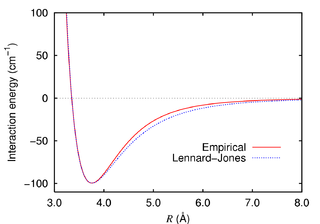
 對應兩個氬原子之間作用的蘭納-瓊斯勢(藍色),與紅色的經驗公式值相差很小。
對應兩個氬原子之間作用的蘭納-瓊斯勢(藍色),與紅色的經驗公式值相差很小。
蘭納-瓊斯勢(英語:Lennard-Jones potential),又稱L-J勢, 6-12勢, 或12-6勢,是用來模擬兩個電中性的分子或原子間相互作用位能的一個比較簡單的數學模型。最早由數學家約翰·蘭納-瓊斯於1924年提出。由於其解析形式簡單而被廣泛使用,特別是用來描述惰性氣體分子間相互作用尤為精確。
蘭納-瓊斯位能以兩體距離為唯一變量,包含兩個參數。其形式為:
![{\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5256ed833acfbaa9f624a55f4be3f9fcb3c27e1a)
ε等於位能井的深度,σ是互相作用的位能正好為零時的兩體距離。在實際應用中,ε、σ參數往往通過擬合已知實驗數據或精確量子計算結果而確定。
另一種寫法是:
![{\displaystyle V(r)=\epsilon \left[\left({\frac {r_{\text{min}}}{r}}\right)^{12}-2\left({\frac {r_{\text{min}}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c2d6edde2238b5eb6fb9ab277141ef922e351f)
 是在位能井底時兩體間距離。
是在位能井底時兩體間距離。
從物理意義上講,第一項 可認為是對應於兩體在近距離時以互相排斥為主的作用,第二項
可認為是對應於兩體在近距離時以互相排斥為主的作用,第二項 對應兩體在遠距離以互相吸引(例如通過范德華力)為主的作用,而此六次方項也的確可以使用以電子-原子核的電偶極矩微擾展開得到。但讀者尤須記住,蘭納-瓊斯勢本身只是一個近似公式。
對應兩體在遠距離以互相吸引(例如通過范德華力)為主的作用,而此六次方項也的確可以使用以電子-原子核的電偶極矩微擾展開得到。但讀者尤須記住,蘭納-瓊斯勢本身只是一個近似公式。
蘭納-瓊斯勢相應的兩體作用力為:

以下是幾種常見的蘭納-瓊斯勢的表示法
此表示法易於模擬軟件的使用

其中 ,
, 。或者
。或者![{\displaystyle \sigma ={\sqrt[{6}]{\frac {A}{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c6b59b78a7e87b148cd7731a87362db88f22715) ,
, 。在此表示法中蘭納-瓊斯勢被寫為12-6勢。[1]
。在此表示法中蘭納-瓊斯勢被寫為12-6勢。[1]
數學上更廣義的形式,包含了一個額外的變數n
![{\displaystyle V_{\text{LJ}}(r)=\epsilon \left[\left({\frac {r_{0}}{r}}\right)^{2n}-2\left({\frac {r_{0}}{r}}\right)^{n}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb7a116d65c8b5a0b3aac6ed4949e335c3ac79b)
其中 是分子間的鍵能(分離原子所需的能量)。
是分子間的鍵能(分離原子所需的能量)。


![{\displaystyle V(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5256ed833acfbaa9f624a55f4be3f9fcb3c27e1a)
![{\displaystyle V(r)=\epsilon \left[\left({\frac {r_{\text{min}}}{r}}\right)^{12}-2\left({\frac {r_{\text{min}}}{r}}\right)^{6}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c2d6edde2238b5eb6fb9ab277141ef922e351f)







![{\displaystyle \sigma ={\sqrt[{6}]{\frac {A}{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c6b59b78a7e87b148cd7731a87362db88f22715)

![{\displaystyle V_{\text{LJ}}(r)=\epsilon \left[\left({\frac {r_{0}}{r}}\right)^{2n}-2\left({\frac {r_{0}}{r}}\right)^{n}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb7a116d65c8b5a0b3aac6ed4949e335c3ac79b)
