三十面体

**三十面体**
部分的三十面体
; 截六角筝形二十四面体	; 对二侧帐塔截角立方体
; 菱形三十面体	; 正十四角反角柱

在几何学中，三十面体是指有30个面的多面体^[1]，在三维空间的三十面体当中没有任何一个形状是正多面体，换言之即正三十面体并不存在，但仍有许多由正多边形组成的三十面体，例如二侧帐塔截角立方体，也有等面的三十面体，例如菱形三十面体。虽然三维空间中不存在正三十面体，但在四维空间中允许三十面体以扭歪正多面体的形式存在（见#扭歪三十面体一节）。部分晶体结构也为三十面体，例如{211}和{100}复合而成的截六角筝形二十四面体^[2]。而三十面体的英语Triacontahedron通常是指菱形三十面体（Rhombic triacontahedron）^[3]^:49。此外要构成三十面体至少要有17个顶点^[4]。

常见的三十面体

常见的三十面体中有一些柱体与锥体以及部分的詹森多面体和均匀多面体的对偶多面体。

截六角筝形二十四面体

截六角筝形二十四面体为截去六个顶点的筝形二十四面体，其中这六个顶点可以对应到立方体的面，其由30个面、72条边和44个顶点组成，在其30个面中，有24个五边形和6个四边形。这个立体是晶体结构{100}（立方体）和{211}（筝形二十四面体）的复合晶体结构，是一种三十面体（30-hedron）。^[2]

二侧帐塔截角立方体

二侧帐塔截角立方体是指在截角立方体的两个八边形面上各叠上一个四角帐塔所构成的几何体。

二侧帐塔截角立方体可以分成两种，一种是叠上一个四角帐塔位于相对的八边形面，称为对二侧帐塔截角立方体；另一种是叠上一个四角帐塔位于截角立方体上两相邻的八边形面，称为邻二侧帐塔截角立方体。其中，对二侧帐塔截角立方体是一种詹森多面体。^[5]

对二侧帐塔截角立方体	邻二侧帐塔截角立方体

菱形三十面体

菱形三十面体（Rhombic triacontahedron）是一个由菱形构成的三十面体^[1]，由30个全等的黄金菱形组成，具有60条边和32个顶点^[6]，其对偶多面体为截半二十面体^[7]^[8]。由于其对偶多面体是一个半正多面体，因此这种立体也属于卡塔兰多面体^[9]。

由于菱形三十面体是一种面可递的立体^[10]，换句话说，即这立体上的任意两个面A和B，若透过旋转或镜射这个立体，使A移动到B原来的位置时，而两个面仍然占据了相同的空间区域^[11]。由于这种特性使得菱形三十面体有时会成为30面骰子的设计^[12]。

二十九角锥

二十九角锥是一种底面为二十九边形的锥体，为三十面体的一种，具有30个面、58条边和30个顶点，其对偶多面体是自己本身^[13]。正二十九角锥是一种底面为正二十九边形的二十九角锥，在施莱夫利符号中可以用{}∨{29}来表示。底边长为 $s$ 、高为 $h$ 的正二十九角锥体积 $V$ 和表面积 $S$ 为^[13]：

V={\frac {29hs^{2}\cot {\frac {\pi }{29}}}{12}}\approx 22.2209hs^{2}

S={\frac {29s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{29}}}}+s\cot {\frac {\pi }{29}}\right)}{4}}\approx 7.25s\left({\sqrt {4h^{2}+84.5452s^{2}}}+9.19485s\right)

二十八角柱

二十八角柱是一种底面为二十八边形的柱体，是三十面体的一种，由30个面和84条边和56个顶点组成，对偶多面体为双二十八角锥。^[14]正二十八角柱代表每个面都是正多边形的二十八角柱，其每个顶点都是2个正方形和1个二十八边形的公共顶点，顶点图以 $4{.}4{.}28$ 表示。其在施莱夫利符号中可以用{28}×{}或t{2,28}来表示，在考克斯特符号（英语：Coxeter-Dynkin diagram）中可以用来表示，在威佐夫符号（英语：Wythoff symbol）中可以利用2 28 | 2来表示，在康威多面体表示法中可以利用P28来表示。底边长为单位长的正二十八角柱体积 $V$ 和表面积 $S$ 为^[14]：

V=7\cot {\frac {\pi }{28}}\approx 62.1267

S=28\left(1+{\frac {\cot {\frac {\pi }{28}}}{2}}\right)\approx 152.253

十四角反角柱

十四角反角柱是一种底面为十四边形的反柱体，是三十面体的一种，由30个面和56条边和28个顶点组成，对偶多面体为十四方偏方面体。^[15]正十四角反角柱代表每个面都是正多边形的十四角反角柱，其每个顶点都是3个正三角形和1个正十四边形的公共顶点，顶点图以 $3{.}3{.}3{.}14$ 表示。其在施莱夫利符号中可以用s{2,28}、sr{2,14}或 $s{\begin{Bmatrix}2\\14\end{Bmatrix}}$ 来表示^[15]，在考克斯特符号（英语：Coxeter-Dynkin diagram）中可以用或来表示，在威佐夫符号（英语：Wythoff symbol）中可以利用| 2 2 14来表示，在康威多面体表示法中可以利用A14来表示。底边长为单位长的正十四角反角柱体积 $V$ 和表面积 $S$ 为^[15]：

V={\frac {7\left(2-{\frac {1}{1+\cos {\frac {\pi }{14}}}}\right)^{\frac {3}{2}}\cot {\frac {\pi }{28}}}{6{\sqrt {2}}}}\approx 13.3655

S=7\left({\sqrt {3}}+\cot {\frac {\pi }{14}}\right)\approx 42.7934

十五方偏方面体

十五方偏方面体是一种以十五边形为底的偏方面体，是三十面体的一种，由30个面和60条边和32个顶点组成，对偶多面体为十五角反角柱。^[16]

星形三十面体

有一些三十面体具有自相交的结构，也就是星形三十面体，例如部分的均匀多面体对偶，大多由考克斯特等人发现^[18]，而鲁洛夫斯（Roelofs）也发现了一种不属于均匀多面体也不是其对偶的星形三十面体，其由6个十二边形和24个正方形组成^[17]。

无穷星形三十面体


小二十面半十二面体的对偶多面体小二十面半无穷星形十二面体（英语：Small icosihemidodecacron）	小十二面半十二面体的对偶多面体小十二面半无穷星形十二面体（英语：Small dodecahemidodecacron）	大二十面半十二面体的对偶多面体大二十面半无穷星形十二面体（英语：Great icosihemidodecacron）	大十二面半十二面体的对偶多面体大十二面半无穷星形十二面体（英语：Great dodecahemidodecacron）	小十二面半二十面体的对偶多面体小十二面半无穷星形二十面体（英语：Small dodecahemicosacron）	大十二面半二十面体的对偶多面体大十二面半无穷星形二十面体（英语：Great dodecahemicosacron）
6个互相相交的无限高十角柱		6个互相相交的无限高十角星柱（英语：Decagrammic prism）		10个互相相交的无限高六角柱

均匀多面体对偶

除了上述六种无穷星形三十面体之外，还有两种均匀多面体的对偶多面体为三十面体，分别为内侧菱形三十面体^[21]和大菱形三十面体^[22]。

内侧菱形三十面体	大菱形三十面体

三十面体列表

名称	种类	符号	顶点	边	面	χ	面的种类	对称性	对偶多面体
二十九角锥	锥体	( )∨{29}	30	58	30	2	1个二十九边形 29个三角形	C_29v, [29], (*29 29)	二十九角锥（自身对偶）
二十八角柱	棱柱体	t{2,28} {28}x{}	56	84	30	2	2个二十八边形 28个矩形	D_28h, [28,2], (*28 2 2)	双二十八角锥
双十五角锥	双锥体	{ }+{15}	17	45	30	2	30个三角形	D_15h, [15,2], (*15 2 2), 60阶	十五角柱
十四角反棱柱	反棱柱	s{2,28} sr{2,14}	28	56	30	2	2个十四边形 28个三角形	D_14d, [2⁺,28], (2*14), 56阶	十四方偏方面体
十四角帐塔	帐塔	{14} \|\| t{14}	42	70	30	2	14个三角形 14个正方形 1个十四边形 1个二十八边形	C_14v, [1,14], (*14 14), order 28
十五方偏方面体	偏方面体	{ }⨁{15}^[23]^:235	32	60	30	2	30个筝形	D_15d, [2⁺,15], (2*15)	十五角反棱柱
对二侧帐塔截角立方体	侧帐塔多面体		32	60	30	2	16个正三角形 10个正方形 4个正八边形	D_4h
邻二侧帐塔截角立方体	侧帐塔多面体		32	60	30	2	16个正三角形 10个正方形 4个正八边形
四侧锥双新月双罩帐	凹多面体		18	46	30	2	2×4+4×5个正三角形 2个正方形
截六角筝形二十四面体	凸多面体		44	72	30	2	24个五角形 6个正方形	O_h, [4,3], *432
小二十面半无穷星形十二面体（英语：Small icosihemidodecacron）	无穷星形多面体		26	60	30	-4	30个抽象四边形	I_h, [5,3], *532	小二十面半十二面体
小十二面半无穷星形十二面体（英语：Small dodecahemidodecacron）	无穷星形多面体		18	60	30	-12		I_h, [5,3], *532	小十二面半十二面体
大二十面半无穷星形十二面体（英语：Great icosihemidodecacron）	无穷星形多面体		26	60	30	-4		I_h, [5,3], *532	大二十面半十二面体
大十二面半无穷星形十二面体（英语：Great dodecahemidodecacron）	无穷星形多面体		18	60	30	-12		I_h, [5,3], *532	大十二面半十二面体
小十二面半无穷星形二十面体（英语：Small dodecahemicosacron）	无穷星形多面体		22	60	30	-8		I_h, [5,3], *532	小十二面半二十面体
大十二面半无穷星形二十面体（英语：Great dodecahemicosacron）	无穷星形多面体		22	60	30	-8		I_h, [5,3], *532	大十二面半二十面体
内侧菱形三十面体	均匀多面体对偶		24	60	30	-6	30个菱形	I_h, [5,3], *532	截半大十二面体
大菱形三十面体	均匀多面体对偶		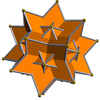32	60	30	2	30个菱形	I_h, [5,3], *532	大截半二十面体

扭歪三十面体

扭歪三十面体是指面与顶点并不存在同一个三维空间而无法确定体积的三十面体，扭歪三十面体仅能存在于四维或以上的空间。

而扭歪三十面体的一个例子为四角六片三角孔扭歪正三十面体，其由30个正方形组成，具有30个面、60条边和20个顶点，在施莱夫利符号中计为{4,6|3}，可以看做是截半五胞体（英语：Runcinated 5-cell）去除所有正三角形面的结果，因此与截半五胞体（英语：Runcinated 5-cell）共用相同的顶点布局。^[24]

参考文献

^ ^1.0 ^1.1 Weisstein, Eric W. (编). Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
^ ^2.0 ^2.1 Barrer, RM and Kerr, IS. 66. Hydrothermal chemistry of the silicates. Part XI. Habit and surface topography in synthetic crystals of the analcite group. Journal of the Chemical Society (Resumed) (Royal Society of Chemistry). 1963: 434–440 [2023-01-09]. doi:10.1039/JR9630000434. （原始内容存档于2022-12-26）.
^ Larkin, N.J. An Introduction to Solid Geometry: And to the Study of Chrystallography ; Containing an Investigation of Some of the Properties Belonging to the Platonic Bodies Independent of the Sphere. 1820 [2022-12-25]. LCCN 06004787. （原始内容存档于2022-12-25）.
^ Counting polyhedra. numericana.com. [2016-01-10]. （原始内容存档于2020-08-20）. （页面存档备份，存于互联网档案馆）
^ Weisstein, Eric W. (编). Biaugmented Truncated Cube. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
^ Can, Zeynep and Kaya, Rüstem; et al. On the metrics induced by icosidodecahedron and rhombic triacontahedron. KoG (Hrvatsko društvo za geometriju i grafiku). 2015, 19 (19.): 17–23.
^ Weisstein, Eric W. (编). Rhombic Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
^ Livio Zefiro, DIP.TE.RIS. Review of the alternative choices concerning face colouring of all the regular convex polyhedra and a pair of Catalan polyhedra, the rhombic dodecahedron and the rhombic triacontahedron. mi.sanu.ac.rs. [2020-08-05]. （原始内容存档于2020-07-11）.
^ The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)
^ Isohedral Rhombohedra. orchidpalms.com. [2020-08-05]. （原始内容存档于2021-04-10）.
^ McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822 .
^ George W. Hart. Polyhedral Dice. Virtual Polyhedra. 1996 [2020-08-05]. （原始内容存档于2021-04-26）.
^ ^13.0 ^13.1 Wolfram, Stephen. "29-gonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ ^14.0 ^14.1 Wolfram, Stephen. "28-gonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ ^15.0 ^15.1 ^15.2 Wolfram, Stephen. "14-antiprism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ Wolfram, Stephen. "15‐trapezohedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ ^17.0 ^17.1 Göbel, Frits. The Taming of Roelofs Polyhedra (PDF). Bridges London: Mathematics, Music, Art, Architecture, Culture. 2006: 105–108 [2023-01-09]. （原始内容存档 (PDF)于2023-01-02）.
^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1954, 246 (916): 401–450. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183. doi:10.1098/rsta.1954.0003.
^ Wenninger, Magnus, Dual Models, Cambridge University Press, 2003 [1983], ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371
^ Wenninger, Dual Models, 2003^[19], Page 101, Duals of the (nine) hemipolyhedra
^ Versi-Regular Polyhedra: Medial Rhombic Triacontahedron. dmccooey.com. [2016-09-01]. （原始内容存档于2016-03-24）.
^ Self-Intersecting Quasi-Regular Duals : Great Rhombic Triacontahedron. dmccooey.com. [2016-08-31]. （原始内容存档于2016-07-31）.
^ Johnson, N.W. Chapter 11: Finite symmetry groups. Geometries and Transformations. 2018. ISBN 978-1-107-10340-5.
^ Klitzing, Richard. Skew polytopes x4o6o|x3o. bendwavy.org.

外部链接

埃里克·韦斯坦因. 三十面體. MathWorld.

[Triacontahedron-1] 1.0 ^1.1 Weisstein, Eric W. (编). Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

[article_barrer196366-2] 2.0 ^2.1 Barrer, RM and Kerr, IS. 66. Hydrothermal chemistry of the silicates. Part XI. Habit and surface topography in synthetic crystals of the analcite group. Journal of the Chemical Society (Resumed) (Royal Society of Chemistry). 1963: 434–440 [2023-01-09]. doi:10.1039/JR9630000434. （原始内容存档于2022-12-26）.

[book_larkin1820introduction-3] Larkin, N.J. An Introduction to Solid Geometry: And to the Study of Chrystallography ; Containing an Investigation of Some of the Properties Belonging to the Platonic Bodies Independent of the Sphere. 1820 [2022-12-25]. LCCN 06004787. （原始内容存档于2022-12-25）.

[4] Counting polyhedra. numericana.com. [2016-01-10]. （原始内容存档于2020-08-20）. （页面存档备份，存于互联网档案馆）

[5] Weisstein, Eric W. (编). Biaugmented Truncated Cube. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

[article_can2015metrics-6] Can, Zeynep and Kaya, Rüstem; et al. On the metrics induced by icosidodecahedron and rhombic triacontahedron. KoG (Hrvatsko društvo za geometriju i grafiku). 2015, 19 (19.): 17–23.

[RhombicTriacontahedron.Mathworld-7] Weisstein, Eric W. (编). Rhombic Triacontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

[Livio_Zefiro,_DIP.TE.RIS-8] Livio Zefiro, DIP.TE.RIS. Review of the alternative choices concerning face colouring of all the regular convex polyhedra and a pair of Catalan polyhedra, the rhombic dodecahedron and the rhombic triacontahedron. mi.sanu.ac.rs. [2020-08-05]. （原始内容存档于2020-07-11）.

[9] The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)

[10] Isohedral Rhombohedra. orchidpalms.com. [2020-08-05]. （原始内容存档于2021-04-10）.

[11] McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822 .

[12] George W. Hart. Polyhedral Dice. Virtual Polyhedra. 1996 [2020-08-05]. （原始内容存档于2021-04-26）.

[29-gonal_pyramid-13] 13.0 ^13.1 Wolfram, Stephen. "29-gonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[28-gonal_prism-14] 14.0 ^14.1 Wolfram, Stephen. "28-gonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[14-antiprism-15] 15.0 ^15.1 ^15.2 Wolfram, Stephen. "14-antiprism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[15‐trapezohedron-16] Wolfram, Stephen. "15‐trapezohedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[inproceedings_gobel2006taming-17] 17.0 ^17.1 Göbel, Frits. The Taming of Roelofs Polyhedra (PDF). Bridges London: Mathematics, Music, Art, Architecture, Culture. 2006: 105–108 [2023-01-09]. （原始内容存档 (PDF)于2023-01-02）.

[18] Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1954, 246 (916): 401–450. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183. doi:10.1098/rsta.1954.0003.

[Wenninger_2003-19] Wenninger, Magnus, Dual Models, Cambridge University Press, 2003 [1983], ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371

[Wenninger_2003_hemipolyhedra-20] Wenninger, Dual Models, 2003^[19], Page 101, Duals of the (nine) hemipolyhedra

[21] Versi-Regular Polyhedra: Medial Rhombic Triacontahedron. dmccooey.com. [2016-09-01]. （原始内容存档于2016-03-24）.

[dmccooeypage-22] Self-Intersecting Quasi-Regular Duals : Great Rhombic Triacontahedron. dmccooey.com. [2016-08-31]. （原始内容存档于2016-07-31）.

[23] Johnson, N.W. Chapter 11: Finite symmetry groups. Geometries and Transformations. 2018. ISBN 978-1-107-10340-5.

[24] Klitzing, Richard. Skew polytopes x4o6o|x3o. bendwavy.org.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[20]

[21]

[22]

[23]

[24]

[19]


小二十面半十二面体的对偶多面体小二十面半无穷星形十二面体（英语：Small icosihemidodecacron）	小十二面半十二面体的对偶多面体小十二面半无穷星形十二面体（英语：Small dodecahemidodecacron）	大二十面半十二面体的对偶多面体大二十面半无穷星形十二面体（英语：Great icosihemidodecacron）	大十二面半十二面体的对偶多面体大十二面半无穷星形十二面体（英语：Great dodecahemidodecacron）	小十二面半二十面体的对偶多面体小十二面半无穷星形二十面体（英语：Small dodecahemicosacron）	大十二面半二十面体的对偶多面体大十二面半无穷星形二十面体（英语：Great dodecahemicosacron）
6个互相相交的无限高十角柱		6个互相相交的无限高十角星柱（英语：Decagrammic prism）		10个互相相交的无限高六角柱

查论编多面体
1 - 10	一面体二面体三面体四面体正四面体锲形体五面体三角柱四角锥六面体立方体长方体四角柱五角锥平行六面体双三角锥七面体八面体九面体十面体
11 - 20	十一面体十二面体十三面体十四面体十五面体十六面体十七面体十八面体十九面体二十面体
其他	空多胞形零面体多面形三面形超二十面体二十二面体二十四面体二十七面体三十面体六十面体无限面体
正多面体	正四面体正六面体正八面体正十二面体正二十面体正无限面体