主題:幾何學
外觀
幾何學

幾何學出現於處理空間關係的知識領域。幾何學是前現代數學的兩個領域之一,另一個是數字的研究。
在近代,幾何學概念已經被擴展。它們有時顯示高水平的抽象和複雜性。幾何學現在使用微積分學和抽象代數的方法,從而使該領域的許多現代分支不容易被辨認出是早期幾何學的後代(見數學領域)。工作於或者是專業從事於幾何學的人是幾何學家。
特色條目
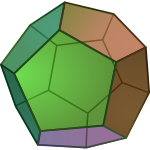
在幾何學中,正圖形又稱正多胞形(英語:Regular polytope),即正幾何圖形,是一種對稱性對於標記可遞的幾何體,且具有高度對稱性,對於該幾何體內所有同維度的元素(如:點、線、面)都完全具有相同的性質,並且每一個元素皆為一個正圖形,例如,正方體所有的面的面積及形狀皆相同,且皆為正方形,是一個二維正多胞形、所有邊的長度也相同,所有角的角度及形式也相同,因此正方體是一個正圖形或正多胞形。對於所有元素,或叫j維面(對所有的 0 ≤ j ≤ n,其中n是該幾何體所在的維度) — 胞、面等等 — 也都對於多胞形的對稱性可遞,也是≤ n維的正圖形。
正圖形是正多邊形(例如,正方形或者正五邊形)和正多面體(例如立方體)的向任意維度的推廣類比。正圖形極強的對稱性使它們擁有極強的審美價值,吸引着數學家和數學愛好者。
一般地,n維正圖形被定義為有正維面[(n − 1)-表面]和正頂點圖。這兩個條件已經能充分地保證所有面、所有頂點都是相似的。但要注意的是,這一定義並不適用於抽象多胞形。
一個正圖形能用形式為{a, b, c, ...., y, z}的施萊夫利符號代表,其正的面為{a, b, c, ..., y},頂點圖為{b, c, ..., y, z}。
相關專題
歡迎參與

- 歡迎改進或擴充的條目 :
- 請求條目:
- 欄目特色圖片, 和精選傳記
- 幾何學綱要、幾何學歷史、合成幾何學、幾何學議題列表、廣義三角函數
- 超矩形、手性 (數學)、偽三角形、抽象多胞形,考克斯特符號、考克斯特元素、421多胞形、E8、錐面、一萬邊形
- 凸幾何、轉換幾何、代數曲面、Gröbner基、實代數幾何、複幾何
- 模板: Template:Honeycombs、Template:Tessellation、Template:Mathematics and art(數學和藝術)
- 需要繼續擴充或翻譯的條目:
- 需要專家關注
- 張量(tensor)
你知道嗎?
分類
以下的分類樹顯示Category:幾何學下的分類。