柯西中值定理,也叫拓展中值定理,是拉格朗日中值定理的推广,是微分学的基本定理之一。
如果函数 及
及 满足
满足
- 在闭区间
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上连续;
上连续;
- 在开区间
 内可微分;
内可微分;
- 对任意
 ;
;
那么在 内至少有一点
内至少有一点 ,使等式
,使等式

或
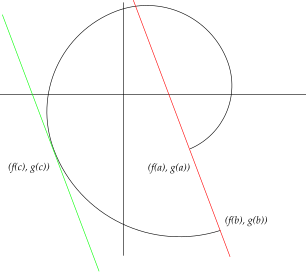 柯西定理的几何意义
柯西定理的几何意义

成立。
其几何意义为:用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。
但柯西定理不能表明在任何情况下不同的两点(f(a),g(a))和(f(b),g(b))都存在切线,因为可能存在一些c值使f′(c) = g′(c) = 0,换句话说取某个值时位于曲线的驻点;在这些点处,曲线根本没有切线。下面是这种情形的一个例子

在区间[−1,1]上,曲线由(−1,0)到(1,0),却并无一个水平切线;然而它有一个驻点(实际上是一个尖点)在t = 0时。
柯西中值定理可以用来证明洛必达法则. 拉格朗日中值定理是柯西中值定理当g(t) = t时的特殊情况。
首先,如果 ,由罗尔定理,存在一点
,由罗尔定理,存在一点 使得
使得 ,与条件3矛盾。所以
,与条件3矛盾。所以 。
。
令 。那么
。那么
 在
在![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上连续,
上连续, 在
在 上可导,
上可导, 。由罗尔定理,存在一点
。由罗尔定理,存在一点 使得
使得 。即
。即 。命题得证。
。命题得证。




![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)















