RLC電路

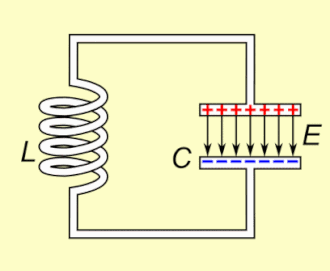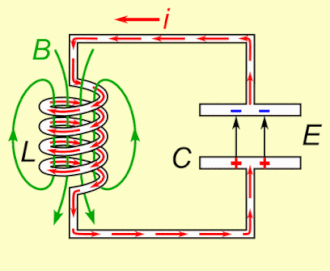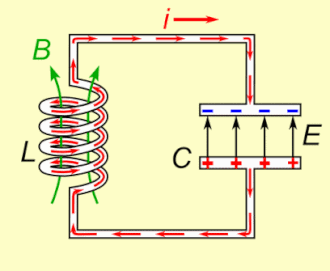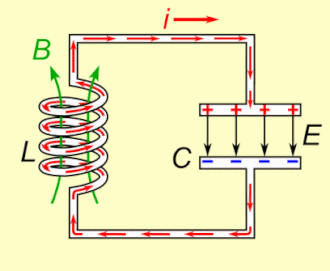
串聯RLC電路：電阻、電感和電容

動畫演示了LC電路（無電阻的RLC電路）的工作。電荷在電容器極板和電感之間來回傳遞。能量在電容器的電場 (E) 和電感的磁場 (B) 之間來回振盪。 RLC電路工作情況類似，不同之處在於，由於電路中的電阻，隨著時間變化振盪電流衰減至零。

RLC電路（英語：RLC circuit）是一種由電阻（R）、電感（L）、電容（C）組成的電路結構。電路的名稱來自於用來表示該電路組成元件的字母，其中元件的順序可能與RLC不同。LC電路是其簡單的例子。RLC電路也被稱為二階電路，電路中的電壓或者電流是一個二階微分方程的解，而其係數是由電路結構決定。

若電路元件都視為線性元件時，一個RLC電路可以被視作電子諧波振盪器。RLC電路作為振盪器電路有很多應用。無線電接收機和電視機通過振盪器電路調諧以從周圍的無線電波中選擇頻率範圍，這種電路通常被稱為調諧電路。

這種電路的固有頻率一般表示為 $f_{c}={1 \over 2\pi {\sqrt {LC}}}$，國際單位為赫茲（Hz）。

RLC電路常用來作帶通濾波器或帶阻濾波器，其Q因子可以由下式得到：

$Q={f_{c} \over B_{W}}={2\pi f_{c}L \over R}={1 \over {\sqrt {R^{2}C/L}}}$

RLC電路的組成結構一般有兩種，分別是串聯型及並聯型。

RLC串聯電路

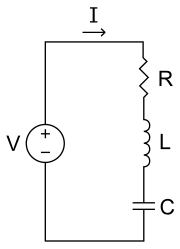
圖 1. RLC串聯電路
V - 電源電壓
I - 電路電流
R - 電阻
L - 電感
C - 電容

在此電路中，三個元件均與電壓以串聯方式連接。其主要的微分方程可將三個元件的本構方程代入基爾霍夫電壓定律（KVL）獲得。由基爾霍夫電壓定律：

$v_{R}+v_{L}+v_{C}=v(t)\,$

其中$\textstyle v_{R},v_{L},v_{C}$分別為R、L、C兩端的電壓，$\textstyle v(t)$為隨時間變化的電源的電壓。將本構方程代入得到：

$RI(t)+L{{dI} \over {dt}}+{1 \over C}\int _{-\infty }^{\tau =t}I(\tau )\,d\tau =v(t)$

在電源電壓為常數的情況下，對上式求導，並且除以L，得到以下二階微分方程：

${{d^{2}I(t)} \over {dt^{2}}}+{R \over L}{{dI(t)} \over {dt}}+{1 \over {LC}}I(t)=0$

此方程可以寫成更常用的形式：

${{d^{2}I(t)} \over {dt^{2}}}+2\alpha {{dI(t)} \over {dt}}+{\omega _{0}}^{2}I(t)=0$

$\alpha \,$稱為「衰減量」，用于衡量當移除外部輸入後，此電路的瞬態響應衰減的速率。$\omega _{0}\,$為角共振頻率。此二係數由下式給出：

$\alpha ={R \over 2L}$ ， $\omega _{0}={1 \over {\sqrt {LC}}}$

阻尼係數$\zeta$是另一個常用的參數，定義為$\alpha \,$與$\omega _{0}\,$的比值：

$\zeta ={\frac {\alpha }{\omega _{0}}}$

阻尼係數也可以由R、L、C求得：

$\zeta ={R \over 2}{\sqrt {C \over L}}$

瞬態響應

圖中顯示了串聯RLC電路的欠阻尼和過阻尼響應。臨界阻尼是用粗紅色曲線畫出的。這些作圖統一都是在 L = 1, C = 1 且 $\scriptstyle \omega _{0}=1\,$ 情況下。

根據不同的阻尼係數$\zeta$的值，該微分方程的解法有三種不同的情況，分別為：欠阻尼（$\scriptstyle \zeta <1\,$），過阻尼（$\scriptstyle \zeta >1\,$），以及臨界阻尼（$\scriptstyle \zeta =1\,$）。該微分方程的特徵方程為：

$s^{2}+2\alpha s+{\omega _{0}}^{2}=0$

該方程的根為：

$s_{1}=-\alpha +{\sqrt {\alpha ^{2}-{\omega _{0}}^{2}}}$

$s_{2}=-\alpha -{\sqrt {\alpha ^{2}-{\omega _{0}}^{2}}}$

該微分方程的通解為兩根指數函數的線性疊加：

$i(t)=A_{1}e^{s_{1}t}+A_{2}e^{s_{2}t}$

係數A₁以及 A₂由具體問題的邊界條件給出。

過阻尼響應

過阻尼響應（$\scriptstyle \zeta >1\,$）為：

$i(t)=A_{1}e^{-\omega _{0}(\zeta +{\sqrt {\zeta ^{2}-1}})t}+A_{2}e^{-\omega _{0}(\zeta -{\sqrt {\zeta ^{2}-1}})t}$

過阻尼響應是一個瞬態電流無振盪的衰減。

欠阻尼響應

欠阻尼響應（$\scriptstyle \zeta <1\,$）為：

$i(t)=B_{1}e^{-\alpha t}\cos(\omega _{d}t)+B_{2}e^{-\alpha t}\sin(\omega _{d}t)\,$

通過三角恆等式，這兩個三角函數可用一個有相位的正弦函數表達：

$i(t)=B_{3}e^{-\alpha t}\sin(\omega _{d}t+\varphi )\,$

欠阻尼響應是一個頻率為$\omega _{d}\,$的衰減的振盪。振盪衰減的速率為$\alpha$。指數里的$\alpha$描述了振盪的包絡函數。B₁ 以及B₂ （或第二種形式中的 B₃ 以及相位差 $\varphi \,$）為任意常數，由邊界條件確定。頻率$\omega _{d}\,$由下式給出：

$\omega _{d}={\sqrt {{\omega _{0}}^{2}-\alpha ^{2}}}=\omega _{0}{\sqrt {1-\zeta ^{2}}}$

這就是所謂的阻尼共振頻率或阻尼固有頻率。它是電路在無外部源驅動時自然振動的頻率。諧振頻率$\omega _{0}\,$是電路在有外部源驅動時的諧振頻率，為了便於區分常稱作無阻尼諧振頻率。

臨界阻尼響應

臨界阻尼響應（$\scriptstyle \zeta =1\,$）為：

$i(t)=D_{1}te^{-\alpha t}+D_{2}e^{-\alpha t}\,$

拉普拉斯域

可以利用拉普拉斯轉換分析RLC串聯電路的交流暫態及穩態行為。若上述電壓源產生的波形，在拉普拉斯轉換後為V(s)（其中s為複頻率$s=\sigma +i\omega \,$），則在拉普拉斯域中應用基爾霍夫電壓定律：

$V(s)=I(s)\left(R+Ls+{\frac {1}{Cs}}\right)$

其中I(s)為拉普拉斯轉換後的電流，求解I(s)：

$I(s)={\frac {1}{R+Ls+{\frac {1}{Cs}}}}V(s)$

在重新整理後，可以得到下式：

$I(s)={\frac {s}{L\left(s^{2}+{R \over L}s+{\frac {1}{LC}}\right)}}V(s)$

拉普拉斯導納

求解拉普拉斯導納Y(s)：

$Y(s)={I(s) \over V(s)}={\frac {s}{L\left(s^{2}+{R \over L}s+{\frac {1}{LC}}\right)}}$

可以利用以上章節定義的參數α及ω_o來簡化上式，可得：

$Y(s)={I(s) \over V(s)}={\frac {s}{L\left(s^{2}+2\alpha s+{\omega _{0}}^{2}\right)}}$

極點和零點

Y(s) 的零點是使得$Y(s)=0$ 的s：

$s=0\,$     及     $|s|\rightarrow \infty$

Y(s) 的極點是使得$Y(s)\rightarrow \infty$ 的s，求解二次方程，可得：

$s=-\alpha \pm {\sqrt {\alpha ^{2}-{\omega _{0}}^{2}}}$

Y(s)的極點即為前文中提到微分方程之特徵方程的根$s_{1}$及$s_{2}$。

正弦穩態

正弦穩態可通過令 $s=j\omega$ 的相量形式來表示，其中 $j$ 為虛數單位。

將此代入上面方程的幅值中：

$\displaystyle |Y(s=j\omega )|={\frac {1}{\sqrt {R^{2}+\left(\omega L-{\frac {1}{\omega C}}\right)^{2}}}}.$

以 ω 為變量的電流的函數為

$\displaystyle |I(j\omega )|=|Y(j\omega )||V(j\omega )|.\,$

有一個峰值$|I(j\omega )|$。在此特殊情況下，這個峰值中的 ω 等於無阻尼固有諧振頻率：

$\omega _{0}={\frac {1}{\sqrt {LC}}}.$

RLC並聯電路

圖 5. RLC 並聯電路
V - 電源電壓
I - 電路電流
R - 電阻
L - 電感
C - 電容

RLC並聯電路的特性可以利用電路的對偶性，將RLC並聯電路視為RLC串聯電路的對偶阻抗來處理，就可以用類似RLC串聯電路的分析方式來分析RLC並聯電路。

RLC並聯電路的衰減量$\alpha \,$可以用下式求得：

$\alpha ={1 \over 2RC}$

而其阻尼係數為：

$\zeta ={1 \over 2R}{\sqrt {L \over C}}$

若不考慮$1/2$的係數，RLC並聯電路的阻尼係數恰好是RLC串聯電路阻尼係數的倒數。

頻域

圖 6. 正弦穩態分析

以R = 1 歐姆、C = 1 法拉、L = 1 亨利、V = 1.0 伏特來進行正規化

將並聯各元件的導納相加，即為此電路的導納：

${1 \over Z}=$  ${1 \over Z_{L}}+{1 \over Z_{C}}+{1 \over Z_{R}}=$  ${1 \over {j\omega L}}+{j\omega C}+{1 \over R}$

電容、電阻及電感並聯後，在共振頻率的阻抗為最大值，和電容、電阻及電感串聯的情形恰好相反，RLC並聯電路是抗共振電路（antiresonator）。

右圖中可以看出若用定電壓驅動時，電流的頻率響應在共振頻率$\omega _{0}={1 \over {\sqrt {LC}}}$處有最小值。若用定電流驅動，電壓的頻率響應在共振頻率處有最大值，和RLC串聯電路中，電流的頻率響應圖形類似。

其他構造

圖7 RLC並聯電路，電阻和電感串聯

圖8 RLC串聯電路，電阻和電容並聯

如圖7所示，電阻與電感串聯的並聯LC電路是有必要考慮到線圈卷線的電阻時經常遇到的一種拓撲結構。並聯LC電路經常用於帶通濾波中，而Q因子主要由此電阻決定。電路的諧振頻率為

$\omega _{0}={\sqrt {{\frac {1}{LC}}-\left({\frac {R}{L}}\right)^{2}}}$

這是電路的諧振頻率，定義為導納虛部為零時的頻率。在特徵方程的一般形式（此電路與之前的相同）中出現的頻率

$s^{2}+2\alpha s+{\omega '_{0}}^{2}=0$

不是相同的頻率。在這種情況下是固有的無阻尼諧振頻率

$\omega '_{0}={\sqrt {\frac {1}{LC}}}$

阻抗幅值最大時的頻率 $\omega _{m}$ 為，

$\omega _{m}=\omega '_{0}{\sqrt {{\frac {-1}{Q_{L}^{2}}}+{\sqrt {1+{\frac {2}{Q_{L}^{2}}}}}}}$

其中$Q_{L}={\frac {\omega '_{0}L}{R}}$是線圈的品質因數。這可以下式很好地近似

$\omega _{m}\approx \omega '_{0}{\sqrt {1-{\frac {1}{2Q_{L}^{4}}}}}$

此外，精確的最大阻抗幅值由下式給出，

$|Z|_{max}=RQ_{L}^{2}{\sqrt {\frac {1}{2Q_{L}{\sqrt {Q_{L}^{2}+2}}-2Q_{L}^{2}-1}}}$.

$Q_{L}$值比1大時，可以用下式很好地近似

$|Z|_{max}\approx {RQ_{L}^{2}}$.

同樣，電阻與電容並聯的串聯LC電路可用於有耗介質的電容器。這種構造如圖8所示。在這種情況下諧振頻率（阻抗的虛部為零時的頻率），由下式給出，

$\omega _{0}={\sqrt {{\frac {1}{LC}}-{\frac {1}{(RC)^{2}}}}}$

而阻抗幅值最大時的頻率 $\omega _{m}$ 為

$\omega _{m}=\omega '_{0}{\sqrt {{\frac {-1}{Q_{C}^{2}}}+{\sqrt {1+{\frac {2}{Q_{C}^{2}}}}}}}$

其中 $Q_{C}=\omega '_{0}{R}{C}$。

參見

• RC電路
• RL電路
• LC電路

參考文獻

來源

• Anant Agarwal, Jeffrey H. Lang, Foundations of analog and digital electronic circuits, Morgan Kaufmann, 2005 ISBN 1-55860-735-8.
• J. L. Humar, Dynamics of structures, Taylor & Francis, 2002 ISBN 90-5809-245-3.
• J. David Irwin, Basic engineering circuit analysis, Wiley, 2006 ISBN 7-302-13021-3.
• Kenneth L. Kaiser, Electromagnetic compatibility handbook, CRC Press, 2004 ISBN 0-8493-2087-9.
• James William Nilsson, Susan A. Riedel, Electric circuits, Prentice Hall, 2008 ISBN 0-13-198925-1.

外部連結

• 串聯RLC交流電路Java模擬（頁面存檔備份，存於網際網路檔案館）