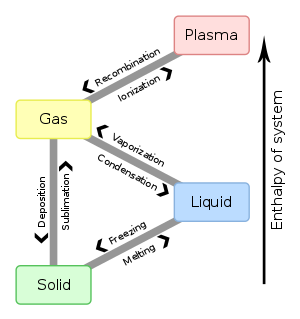
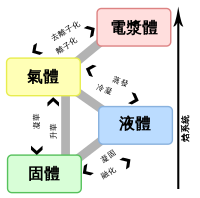
相變
相變,又稱物態變化,是指物質在外部參數(如:溫度、壓力、磁場等等)連續變化之下,從一種相(態)忽然變成另一種相,最常見的是冰變成水和水變成蒸氣。

然而,除了物體的三相變化(固態、液態、氣態)自然界還存在許許多多的相變現象,例如日常生活中另一種較常見的相變是加熱一塊磁鐵,磁鐵的鐵磁性忽然消失。其他在物理學中重要相變列舉如下:
相變的種類
[編輯]第一個嘗試將相變加以分類的是奧地利數學家、物理學家保羅·埃倫費斯特。相變分為一級相變和二級相變甚至多級相變,從數學角度講,一級相變的熱力學函數連續,但其狀態函數的一階導數不連續。二級相變的熱力學函數及其關於狀態函數的一階導數都連續,但其關於狀態函數的二階導數不連續。從理論角度來看,一級相變在相變發生時,兩相之間有潛熱和體積等躍變。二級相變在相變發生時,兩相之間無潛熱和體積躍變,但有熱容躍變。
相變的特性
[編輯]對稱破缺
[編輯]對稱性破缺(symmetry breaking)係指物理學裡,在具有某種對稱性的物理系統之臨界點附近發生可能分岔中的一個分岔,打破了這物理系統的對稱性,並且決定了這物理系統的命運。例如當水溫降至接近冰點時,水中各處看起來皆相同,因此水系統具有空間上的對稱性,此時若某處的溫度振盪至低於冰點,便破壞了對稱性,且決定了所凝固之冰的結構。對於外在觀察者,不清楚有漲落(或熱噪聲)的存在,會覺得這選擇相當隨機或任意。在圖樣形成(pattern formation)里,對稱性破缺占有重要角色。
對稱性破缺可以分為兩種:
明顯對稱性破缺:在描述物理系統的拉格朗日量或哈密頓量的數學表示里,存在明顯不具有某種對稱性的項。 自發對稱性破缺:描述物理系統的拉格朗日量或哈密頓量具有某種對稱性,但是物理系統的最低能量態(真空態)不具有此種對稱性。通常,這種對稱性破缺會具有一種有序參數。動力學對稱性破缺是這種對稱性破缺的特例。著名例子分別為標準模型中的希格斯機制、超導物理中的BCS理論。
序參量
[編輯]序參量是order parameter。
臨界指數和普適類
[編輯]臨界指數是指,臨界點附近,定量描述物理量的臨界行為時所使用的指數常數。
例子
[編輯]- 易辛模型(可以用共形場論計算臨界指數)
- 別列津斯基-科斯特利茨-索利斯相變
參考文獻
[編輯]- Peskin Schroeder, Quantum Field Theory
- Kardar, Statistical Theory of Fields
- Kleiner, Critical properties of phi fourth theories
- Zinn Justin, Critical phenomena