機率分布

「Probability distribution」的各地常用名稱
「Probability distribution」的各地常用名稱
中國大陸	概率分布
臺灣	機率分布、機率分配
港澳	概率分佈
日本、韓國漢字	確率分布

機率分布（英語：probability distribution）簡稱分布，亦稱機率分配或分配，是機率論中的一個概念。

使用時可以有以下兩種含義：

廣義地，它指稱：隨機變數的機率性質——當我們說機率空間 $(\Omega ,{\mathcal {F}},\mathbb {P} )$ 中的兩個隨機變數X和Y具有同樣的分布時，我們是無法用機率 $\mathbb {P}$ 來區別他們的。換言之：

稱X和Y為同分布的隨機變數，若且唯若對任意事件 $A\in {\mathcal {F}}$ ，有 $\mathbb {P} (X\in A)=\mathbb {P} (Y\in A)$ 成立。

但是，不能認為同分布的隨機變數是相同的隨機變數。事實上即使X與Y同分布，也可以沒有任何點ω使得X(ω)=Y(ω)。在這個意義下，可以把隨機變數分類，每一類稱作一個分布，其中的所有隨機變數都同分布。用更簡要的語言來說，同分布是一種等價關係，每一個等價類就是一個分布。需注意的是，通常談到的離散分布、均勻分布、伯努利分布、常態分布、卜瓦松分布等，都是指各種類型的分布，而不能視作一個分布。

狹義地，它是指：隨機變數的機率分布函數。設X是樣本空間 $(\Omega ,{\mathcal {F}})$ 上的隨機變數， $\mathbb {P}$ 為機率測度，則稱如下定義的函數是X的分布函數，或稱累積分布函數：

$F_{X}(a)=\mathbb {P} (X\leq a)$ ，對任意實數 $a$ 定義。

具有相同分布函數的隨機變數一定是同分布的，因此可以用分布函數來描述一個分布，但更常用的描述手段是機率密度函數。^{[註 1]}

分布函數的性質刻劃

對於特定的隨機變數 $X$ ，其分布函數 $F_{X}$ 是單調不減及右連續，而且 $F_{X}(-\infty )=0$ ， $F_{X}(\infty )=1$ 。這些性質反過來也描述了所有可能成為分布函數的函數：

設 $F:[-\infty ,\infty ]\to [0,1],F(-\infty )=0,F(\infty )=1$ 且單調不減、右連續，則存在機率空間 $(\Omega ,{\mathcal {F}},\mathbb {P} )$ 及其上的隨機變數 X ，使得 F 是 X 的分布函數，即 $F_{X}=F$

隨機變數的分布

設 $P$ 為機率測度， $X$ 為隨機變數，則函數 $F(x)=P(X\leq x),(x\in \mathbb {R} )$ 稱為 $X$ 的機率分布函數。如果將 $X$ 看成是數軸上的隨機點的坐標，那麼，分布函數 $F(x)$ 在 $x$ 處的函數值就表示 $X$ 落在區間 $(-\infty ,x]$ 上的機率。

例如，設隨機變數 $X$ 為擲兩次骰子所得的點數差，而整個樣本空間由 36 個元素組成。

數量	( i , j )∈ S	$x$	$P(X=x)$	$F(x)$
6	( 1,1 )，( 2,2 )，( 3,3 ) ( 4,4 )，( 5,5 )，( 6,6 )	0	6/36	6/36
10	( 1,2 )，( 2,3 ) ( 3,4 )，( 4,5 )，( 5,6 ) ( 2,1 )，( 3,2 )，( 4,3 ) ( 5,4 )，( 6,5 )	1	10/36	16/36
8	( 1,3 )，( 2,4 )，( 3,5 ) ( 4,6 )，( 3,1 )，( 4,2 ) ( 5,3 )，( 6,4 )	2	8/36	24/36
6	( 1,4 )，( 2,5 )，( 3,6 ) ( 4,1 )，( 5,2 )，( 6,3 )	3	6/36	30/36
4	( 1,5 )，( 2,6 ) ( 5,1 )，( 6,2 )	4	4/36	34/36
2	( 1,6 )，( 6,1 )	5	2/36	36/36

其分布函數是：

F(x)={\begin{cases}0,x<0\\6/36,x<1\\16/36,x<2\\24/36,x<3\\30/36,x<4\\34/36,x<5\\1,x\geq 5\end{cases}}

離散機率分布族

上面所列舉的例子屬於離散分布，即分布函數的值域是離散的，比如只取整數值的隨機變數就是屬於離散分布的。 $F(x)$ 表示隨機變數 $X\leq x$ 的機率值。如果X的取值只有 $x_{1}<x_{2}<...<x_{n}$ ，則：

$F_{X}(x_{i})=\sum _{j=1}^{i}P(x_{j})$
$\sum _{k=1}^{n}P(x_{k})=1$

其他常見的離散機率分布族有：

伯努利分布

二項式分布

二項分布是最重要的離散機率分布之一，由瑞士數學家雅各布·伯努利所發展，一般用二項分布來計算機率的前提是，每次抽出樣品後再放回去，並且只能有兩種試驗結果，比如黑球或紅球，正品或次品等。二項分布指出，隨機一次試驗出現的機率如果為 $p$ ，那麼在 $n$ 次試驗中出現 $k$ 次的機率為：

f(n,k,p)={n \choose k}p^{k}(1-p)^{n-k}

例如，在擲3次骰子中，不出現6點的機率是： $f(3,0,{\frac {1}{6}})={3 \choose 0}\left({\frac {1}{6}}\right)^{0}\left({\frac {5}{6}}\right)^{3}=0.579$
在連續兩次的輪盤遊戲中，至少出現一次紅色的機率為： $f(2,1,{\frac {18}{37}})+f(2,2,{\frac {18}{37}})=0.736$

二項分布在 $p=0.5$ 時表現出圖像的對稱性，而在 $p$ 取其它值時是非對稱的。另外二項分布的期望值 $\operatorname {E} (X)=np$ ，以及變異數 $\operatorname {var} (X)=n\,p\,(1-p)\!$

幾何分布

負二項式分布

超幾何分布

作為離散機率分布的超幾何分布尤其指在抽樣試驗時抽出的樣品不再放回去的分布情況。在一個容器中一共有 $N$ 個球，其中 $M$ 個黑球， $(N-M)$ 個紅球，通過下面的超幾何分布公式可以計算出，從容器中抽出的 $n$ 個球中（抽出的球不放回去）有 $k$ 個黑球的機率是多少：

f(k,n;M;N):={\frac {\displaystyle {M \choose k}{N-M \choose n-k}}{\displaystyle {N \choose n}}}

例如，容器中一共10個球，其中6個黑色，4個白色，一共抽5次（抽出的球不放回去），在這5個球中有3個黑球的機率是： $f(k=3)={\frac {\displaystyle {6 \choose 3}{10-6 \choose 5-3}}{\displaystyle {10 \choose 5}}}=0.476$

超幾何分布與二項式分布的關係

與二項式分布不同的是，在超幾何分布中，特別強調的是抽出的樣品在下一次抽取前不再放回去，但是如果抽取的次數 $n$ 和總共樣品數 $N$ 相比很小（大約 $n/N<0.05$ ），這時在計算上二項分布和超幾何分布相互間則沒有主要的區別，此時人們更願意採用二項分布的方法，因為在數學計算上二項分布要簡單一些。

Poisson分布

Poisson近似是二項分布的一種極限形式。其強調如下的試驗前提：一次抽樣的機率值 $p$ 相對很小，而抽取次數 $n$ 值又相對很大。因此卜瓦松分布又被稱之為罕有事件分布。卜瓦松分布指出，如果隨機一次試驗出現的機率為 $p$ ，那麼在 $n$ 次試驗中出現 $k$ 次的機率按照卜瓦松分布應該為：

f(n,k,p)={\frac {(n\cdot p)^{k}}{e^{n\cdot p}\cdot k!}}

其中，數學常數 $e=2.71828...$ (自然對數的底數)
例如，某工廠在生產零件時，每200個成品中會有1個次品，那麼在100個零件中最多出現2個次品的機率按照卜瓦松分布應該是： $f(100,0,{\frac {1}{200}})+f(100,1,{\frac {1}{200}})+f(100,2,{\frac {1}{200}})=0.986$

在實踐中如果遇到 $n$ 值很大導致二項分布難於計算時，可以考慮使用卜瓦松分布，但前提是 $n\cdot p$ 必須趨於一個有限極限^{[來源請求]}。採用卜瓦松分布的一個不太嚴格的規則（通過展開二項分布，並在形式上化簡為類似卜瓦松分布後，利用極限化簡即可得）^{[來源請求]}是：

$n\geq 100$
$p\leq 0.1$

離散均勻分布

連續機率分布族

設 $X$ 是具有分布函數 $F$ 的連續隨機變數，且F的一階導數處處存在，則其導函數

f(x)={\frac {\operatorname {d} F(x)}{\operatorname {d} x}}

稱為 $X$ 的機率密度函數。
每個機率密度函數都有如下性質：

$\int _{-\infty }^{\infty }f(x)\,{\rm {d}}x=1$
$\int _{a}^{b}f(x)\,{\rm {d}}x=\operatorname {P} (a\leq X\leq b)=F(b)-F(a)$

第一個性質表明，機率密度函數與 $x$ 軸形成的區域的面積等於1，第二個性質表明，連續隨機變數在區間 $[a,b]$ 的機率值等於密度函數在區間 $[a,b]$ 上的積分，也即是與 $X$ 軸在 $[a,b]$ 內形成的區域的面積。因為 $0\leq F(x)\leq 1$ ，且 $f(x)$ 是 $F(x)$ 的導數，因此按照積分原理不難推出上面兩個公式。

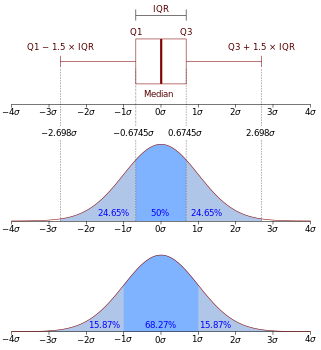
常態分布、指數分布、 $t$ -分布， $F$ -分布以及 $\chi ^{2}$ -分布都是連續分布。

常見的連續機率分布族有：

均勻分布

常態分布

連續隨機變數的機率密度函數如果是如下形式，

f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\left(-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}\right)}

那麼這個連續分布被稱之為常態分布，或者高斯分布。其密度函數的曲線呈對稱鐘形，因此又被稱之為鐘形曲線，其中 $\mu$ 是平均值， $\sigma$ 是標準差。常態分布是一種理想分布，許多典型的分布，比如成年人的身高，汽車輪胎的運轉狀態，人類的智商值（IQ），都屬於或者說至少接近常態分布。同樣按照連續分布的定義，常態機率密度函數具有和普通機率密度函數類似的性質：

$\int _{-\infty }^{\infty }f(t)\,{\rm {d}}t=1$
$F(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}e^{\left(-{\frac {1}{2}}\left({\frac {t-\mu }{\sigma }}\right)^{2}\right)}\,{\rm {d}}t$

如果給出一個常態分布的平均值 $\mu$ 以及標準差 $\sigma$ ，可以根據上面的第二個公式計算出任一區間的機率分布情況。但是如上的計算量是相當龐大的，沒有計算機的輔助基本是不可能的，解決這一問題的方法是藉助 $z$ -轉換以及標準常態分布表格（ $z$ -表格）。

中間值 $\mu =0$ 以及標準差 $\sigma =1$ 的常態分布被稱之為標準常態分布，其累積分布函數是

\Phi (z)={\frac {1}{\sqrt {2\pi }}}\cdot \int _{-\infty }^{z}e^{-{\frac {1}{2}}t^{2}}\mathrm {d} t

將普通形式的常態分布轉換到標準常態分布的方法是

z={\frac {x-\mu }{\sigma }}

例如，已知 $X$ 服從常態分布，且 $\mu =5$ ， $\sigma =3$ ，求區間機率值 $P(4<X\leq 7)$ 。計算過程如下：

設另一隨機變數 $Z={\frac {X-5}{3}}$ ，則 $Z$ 服從標準常態分布，且

{\begin{aligned}&\qquad \quad 4<X\leq 7\\&\iff {\frac {4-5}{3}}<Z\leq {\frac {7-5}{3}}\\&\iff -1/3<Z\leq 2/3,\end{aligned}}

所以

P(4<X\leq 7)=P(-1/3<Z\leq 2/3)=\Phi (2/3)-\Phi (-1/3)\approx 0.7475-0.3694=0.3781,

其中 $\Phi (z)$ 值通過查 $z$ -表格獲得。

常態分布與二項分布的關係

在離散分布中如果試驗次數 $n$ 值非常大，而且單次試驗的機率 $p$ 值又不是很小的情況下，常態分布可以用來近似的代替二項分布。一個粗略的使用常態分布的近似規則是： $n\cdot p\cdot (1-p)\geq 9$ 。
從二項分布中獲得 $\mu$ 和 $\sigma$ 值的方法是

期望值 $\mu =n\cdot p$
標準差 $\sigma ={\sqrt {n\cdot p\cdot (1-p)}}$

如果 $\sigma >3$ ，則必須採用下面的近似修正方法：

P(x_{1}\leq X\leq x_{2})=\underbrace {\sum _{k=x_{1}}^{x_{2}}{n \choose k}\cdot p^{k}\cdot (q)^{n-k}} _{\mathrm {EF} }\approx \underbrace {\Phi \left({\frac {x_{2}+0.5-\mu }{\sigma }}\right)-\Phi \left({\frac {x_{1}-0.5-\mu }{\sigma }}\right)} _{\mathrm {ZF} }

（註： $q=1-p$ ；EF：二項分布；ZF：常態分布）

上（下）臨界值分別增加（減少）修正值0.5的目的是在 $\sigma$ 值很大時獲得更精確的近似值，只有 $\sigma$ 很小時，修正值0.5可以不被考慮。

例如，隨機試驗為連續64次擲硬幣，獲得的國徽數位於32和42之間的機率是多少？用常態分布計算如下，

\mu =n\cdot p=64\cdot 0.5=32

\sigma ={\sqrt {n\cdot p\cdot (1-p)}}={\sqrt {64\cdot 0.5\cdot 0.5}}=4

$n\cdot p\cdot q=16\geq 9$ ，符合近似規則，應用 $z$ -轉換：

P(32\leq X\leq 42)\approx \Phi \left({\frac {42+0.5-32}{4}}\right)-\Phi \left({\frac {32-0.5-32}{4}}\right)

=\Phi \left(2.63\right)-\Phi \left(-0.13\right)=0.0517+0.4957=0.5474

在運用 $z$ -表格時注意到利用密度函數的對稱性來求出 $z$ 為負值時的區域面積。

伽瑪分布

指數分布

其他連續型常用分布

貝它分布

雙指數分布

對數常態分布

柏拉圖分布

柯西分布

多元常態分布

參考文獻

彼得·缺菲爾（Peter Zoefel）：《統計和經濟學家》（德文）. PEASON Studium出版社，2003年. ISBN 3-8273-7062-0.
約瑟夫·西拉（Josef Schira）：《統計理論與企業管理》（德文）. PEASON Studium出版社，2003年. ISBN 3-8273-7041-8.
漢斯-底特·黑伯曼（Hans-Dieter Hippmann）：《統計學》（德文）. SCHAEFFER POESCHEL出版社，2003年. ISBN 3-7910-2119-2.

參見

注釋

^ 在常用的文獻中，「分布」一詞可指其廣義和狹義，而「累計分布函數」或「分布函數」一詞只能指稱後者。為了不致混淆，下文中談及上述的廣義時使用「分布」一詞；狹義時使用「分布函數」一詞。

外部連結

機率分布Java演示

[1] 在常用的文獻中，「分布」一詞可指其廣義和狹義，而「累計分布函數」或「分布函數」一詞只能指稱後者。為了不致混淆，下文中談及上述的廣義時使用「分布」一詞；狹義時使用「分布函數」一詞。

[註 1]

閱論編機率分布的理論
機率質量函數(pmf) 機率密度函數(pdf) 累積分布函數(cdf) 分位函數
動差主動差期望值變異數標準差偏度峰度
動差生成函數(mgf) 特徵函數機率生成函數(pgf) 累積量

閱論編常見一元（英語：Univariate distribution）機率分布
連續	Β 柯西 χ² 指數 F Γ 拉普拉斯對數常態常態柏拉圖學生t 均勻韋伯
離散	伯努利二項離散均勻幾何超幾何負二項卜瓦松
機率分布列表（英語：List of probability distributions）