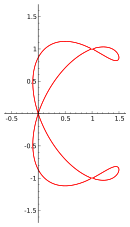
四次平面曲線
四次平面曲線(quartic plane curve)是四次的平面代數曲線,可以表示為以下的多變數四次方程:
A, B, C, D, E中至少要有一個不為0。方程式有15個常數,不過方程式若乘以非零的任意數,不會改變曲線,因此可以將其中一個常數固定為1,留下14個可調整的常數。四次曲線的空間可以視為是的實射影空間。依照克萊姆定理,若考慮一般位置下14個不同的點,通過這十四個點的四次平面曲線唯一,因此四次平面曲線的自由度為14。
四次曲線最多可以有:
也可以考慮在其他數學域(甚至是環)中的四次曲線,例如在複數中的四次曲線。此時可以得到黎曼曲面,在C上是一維的物件,但在R上是二維的物件。例如Klein四次曲線,另外也可以探討射影平面下的曲線,由齊次多項式所定義。
舉例
[編輯]上述曲線中,係數的不同組合產生了以下重要的曲線族。
|
|
|
&符號曲線
[編輯]&符號曲線(ampersand curve)是以下方程對應的四次曲線
Bean曲線
[編輯]Bean曲線(bean curve)是以下方程對應的四次曲線
其虧格為0,在原點有一個奇點,是一個一般的三次點[2] [3]。
Bicuspid曲線
[編輯]bicuspid是方程式如下的四次曲線:
其中a決定了曲線的大小。 bicuspid只有二個node為奇異點,因此是虧格為1的曲線。 [4]
Bow曲線
[編輯]Bow曲線是方程式如下的四次曲線:
在x=0, y=0處有單一的三重點,是有理曲線,虧格為0。 [5]
Cruciform曲線
[編輯]Cruciform曲線是以下方程的四次曲線
其中a和b為決定曲線形狀的參數。 Cruciform曲線可以透過一個標準的二次變換x ↦ 1/x, y ↦ 1/y轉變為橢圓a2x2 + b2y2 = 1,因此是虧格為0的有理平面代數曲線。Cruciform曲線在實射影平面中有三個雙重點,是(x=0、y=0),(x=0 、z=0) 以及(y=0、z=0)。 [6]
此曲線是有理曲線,參數化後的結果也是有理函數。例如,令a=1及b=2,可得以下的參數式
其中唯一一個無法參數化的點是會讓參數式分母為零的點。
Spiric截面
[編輯]Spiric截面可以定義成對x軸及y軸對稱的圓代數四次平面曲線。Spiric截面包括在環面曲線中,其中包括了hippopede及卡西尼卵形線。其英文名稱Spiric源自古希臘文的環面σπειρα。
笛卡兒坐標系下的方程式為
極座標系的方程式為
三葉線
[編輯]三葉線(three-leaved clover)是以下方程的四次平面曲線
在求解y後,曲線可以表示為以下的方程:
其中二個±是彼此獨立的,因此每一個x會對應四個y值。
三葉線的參數式為
在極坐標(x = r cos φ, y = r sin φ)下的方程如下
這是玫瑰線中k = 3的特例。 三葉線在原點處為三重點,有三個二切線。
參考資料
[編輯]- ^ Weisstein, Eric W. (編). Ampersand Curve. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Cundy, H. Martyn; Rollett, A. P., Mathematical models 2nd, Clarendon Press, Oxford: 72, 1961 [1952], ISBN 978-0-906212-20-2, MR 0124167
- ^ 埃里克·韋斯坦因. Bean Curve. MathWorld.
- ^ Weisstein, Eric W. (編). Bicuspid Curve. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Weisstein, Eric W. (編). Bow. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Weisstein, Eric W. (編). Cruciform curve. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Gibson, C. G., Elementary Geometry of Algebraic Curves, an Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, ISBN 978-0-521-64641-3. Pages 12 and 78.