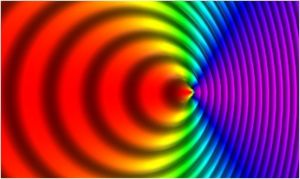
 一个光源向右移动,速度为0.7c。频率在右面较高,在左面较低。
一个光源向右移动,速度为0.7c。频率在右面较高,在左面较低。
相对论性多普勒效应描述了光因为波源与观察者的相对运动关系(一如寻常版的多普勒效应)而有的频率(以及波长)上的变化,而在这里又多考虑了狭义相对论带来的效应。
相对论性多普勒效应和非相对论性版本的多普勒效应有许多不同之处,例如其方程式纳入了狭义相对论中的时间展长效应。这些方程式描述了所观察到的完全频率差值,并具有相对论要求的洛仑兹对称性。
假设观察者(Observer)与波源(Source)是以一相对速度 彼此远离,并从波源的参考系来考虑这个问题。
彼此远离,并从波源的参考系来考虑这个问题。
当某一波前抵达观察者处,则下一个最接近的波前距离观察者有 (其中
(其中 是波长、
是波长、 是波源所发出的原始光波频率、
是波源所发出的原始光波频率、 是光速)。由于波前移动速度(即光波移动速度)为
是光速)。由于波前移动速度(即光波移动速度)为 而观察者远离速度为
而观察者远离速度为 ,观察者接收一个完整的波(或经历两个波前)需历时:
,观察者接收一个完整的波(或经历两个波前)需历时:

当物体以相对高速移动时,需考虑相对论的时间展长效应,故观察者测量到的时间会是:

其中 ,所以观察者测量到的频率是:
,所以观察者测量到的频率是:
 。
。
若观察者与波源正以速度 彼此远离,则观察到的频率
彼此远离,则观察到的频率 会与波源发出的频率
会与波源发出的频率 相异,关系式可写作:
相异,关系式可写作:

其中 是真空中光速。
是真空中光速。
相应的波长关系式则可写作:

所导致的红移 可写作
可写作

在非相对论极限下,亦即当 ,近似式可写作:
,近似式可写作:

注:此段落所假设的是观察者和波源互相“远离”。若他们是互相“接近”,则 需设为负值。
需设为负值。
若从观察者参考系来看,波源以速度 以及相对于从观察者到波源方向呈一个角度
以及相对于从观察者到波源方向呈一个角度 (光从参波源发射到观察者方向与波源速度的夹角)远离,则频率变化为
(光从参波源发射到观察者方向与波源速度的夹角)远离,则频率变化为

其中
然而,若角度 是在波源参考系量测到的(光从参波源发射到观察者方向于观察者速度的夹角),则表示式为
是在波源参考系量测到的(光从参波源发射到观察者方向于观察者速度的夹角),则表示式为

在非相对论极限下:
 。
。























