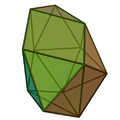
广底加长型球状屋顶
 | |||
| 类别 | 约翰逊多面体 J88 - J89 - J90 | ||
|---|---|---|---|
| 识别 | |||
| 名称 | 广底加长型球状屋顶 Hebesphenomegacorona | ||
| 别名 | 広底長球形屋根(日语) | ||
| 参考索引 | J89 | ||
| 鲍尔斯缩写 | hawmco | ||
| 性质 | |||
| 面 | 21 | ||
| 边 | 33 | ||
| 顶点 | 14 | ||
| 欧拉特征数 | F=21, E=33, V=14 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 3×2+3×4个三角形 1+2个正方形 | ||
| 顶点图 | 4个(32.42) 2+2×2个(35) 4个(34.4) | ||
| 对称性 | |||
| 对称群 | C2v群 | ||
| 特性 | |||
| 凸 | |||
| 图像 | |||
| |||
广底加长型球状屋顶(日语:広底長球形屋根、英语:Hebesphenomegacorona)是一种由18个三角形和3个正方形组成的二十一面体[1],为约翰逊多面体的其中一个,索引为J89[2]。它无法由帕雷托立体(正多面体)和阿基米得立体(半正多面体)经过切割、增补而得来,是约翰逊多面体中的基本立体之一。约翰逊多面体是凸多面体,面皆由正多边形组成但不属于均匀多面体,共有92种。这些立体最早在1966年由诺曼·约翰逊(Norman Johnson)命名并给予描述[3]。
性质
[编辑]广底加长型球状屋顶共由21个面、33条边和14个顶点所组成[4][5][6][7]。在其21个面中,有18个三角形和3个正方形[5][7]。在其14个顶点中,6个顶点是5个三角形的公共顶点[7],在顶点图中可以用[35]来表示[8]、还有4个顶点是4个三角形和1个正方形的公共顶点[7],在顶点图中可以用[34,4]来表示[8]、剩下的4个顶点是2个三角形和2个正方形的公共顶点[7],在顶点图中可以用[32,42]来表示[8]。
体积与表面积
[编辑]而其体积约为2.9129104145402091660[5]。
顶点坐标
[编辑]令 ≈ 0.216844815713457为下列多项式的第二小实根:[6]
则边长为2的广底加长型球状屋顶的顶点坐标为:[6]
其中,、、、和分别为:[6]
这些坐标也可以由下列顶点的轨道的并集在沿xz平面和yz平面镜射所产生的空间对称群之群作用下给出:[11]
相关多面体
[编辑]广底加长型球状屋顶欠侧锥
[编辑]广底加长型球状屋顶欠侧锥(Diminished hebesphenomegacorona)是指从广底加长型球状屋顶上移除一个五角锥所构成的立体,然而,直接将五角锥从广底加长型球状屋顶移除将会出现一个不共面五边形,无法构成多面体,需要将顶点位置些微调整,才能将五边形面放置到移除五角锥的位置,这将导致广底加长型球状屋顶欠侧锥的面仅是很接近正多边形而不是正多边形,因此是一种拟约翰逊多面体。
-
广底加长型球状屋顶
-
广底加长型球状屋顶欠侧锥
-
广底加长型球状屋顶欠侧锥的3D模型
其他立体
[编辑]参见
[编辑]参考文献
[编辑]- ^ Santiago Alvarez. Polyhedra in (Inorganic) Chemistry (PDF). Electronic Supplementary Information for Dalton Transactions. 2005 [2022-09-25]. (原始内容存档 (PDF)于2022-01-21).
- ^ Weisstein, Eric W. (编). Hebesphenomegacorona. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ V.Bulatov. sphenomegacorona. [2022-09-11]. (原始内容存档于2022-09-11).
- ^ 5.0 5.1 5.2 David I. McCooey. Johnson Solids: Hebesphenomegacorona. [2022-09-07].
- ^ 6.0 6.1 6.2 6.3 The Hebesphenomegacorona. qfbox.info. [2022-09-11]. (原始内容存档于2022-09-11).
- ^ 7.0 7.1 7.2 7.3 7.4 Hebesphenomegacorona. polyhedra.tessera.li. [2022-09-11]. (原始内容存档于2022-09-11).
- ^ 8.0 8.1 8.2 Richard Klitzing. hebesphenomegacorona, hawmco. bendwavy.org.
- ^ Wolfram, Stephen. "Hebesphenomegacorona". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020.
PolyhedronData[{"Johnson", 89}, "SurfaceArea"] - ^ Timofeenko, A. V. The non-platonic and non-Archimedean noncomposite polyhedra. Journal of Mathematical Sciences. 2009-10-17, 162 (5): 710–729. ISSN 1072-3374. S2CID 120114341. doi:10.1007/s10958-009-9655-0.