龍伯透鏡

標準龍伯透鏡的橫截面

龍伯透鏡（Luneburg lens），是一種球面對稱梯度折射率透鏡。它由無損介電材料製成的實心球體組成，其介電常數與位置相關。如果其背面是鏡面，它會將入射的平行波準確地反射到其源頭方向，從而充當反射器的作用。典型的龍伯透鏡的折射率n從中心到外表面呈徑向減小。它們可用於從可見光到無線電波的電磁輻射。

對於某些折射率分佈，透鏡將形成兩個給定同心球的完美幾何圖像。有無數種折射率分佈可以產生這種效果。最簡單的解決方案是由數學家魯道夫·龍伯於1944年提出的。 龍伯的折射率解決方案在透鏡外產生兩個共軛焦點。如果一個焦點位於無窮遠處，另一個焦點位於透鏡的另一側表面，則該解決方案採用簡單而明確的形式。J. Brown和A. S. Gutman隨後提出了產生一個內部焦點和一個外部焦點的解決方案。 這些解決方案並不是唯一的；解決方案集由一組必須進行數值評估的定積分定義。

龍伯透鏡是由若干層介電常數不同的材料製成的介質球，能使照射在透鏡上的電磁波，通過透鏡聚焦在金屬反射面的內表面上，經過反射，將反射波通過透鏡返回發射源方向。主要用以產生假目標欺騙雷達。龍伯透鏡反射器具有體積小，雷達截面積比相同尺寸的角反射器大，在水平和垂直方向上具有較寬的反射方向圖等優點，但重量重、造價貴、製造工藝複雜。

設計

龍伯解決方案

當光源位於其邊緣時，龍伯透鏡會將點光源轉換為準直光束。

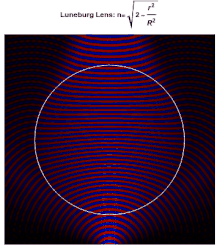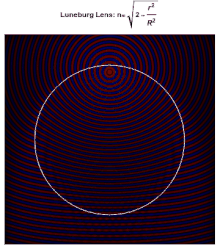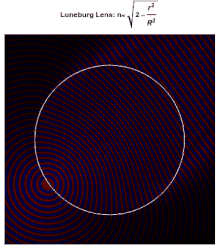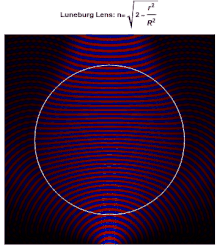
理想龍伯透鏡表面上的每個點都是入射到對側的平行輻射的焦點。理想情況下，根據以下公式，透鏡組成材料的介電常數$\epsilon _{r}$從中心的2降至表面的1（或者等效地，折射率$n$從${\sqrt {2}}$降至1）

$n={\sqrt {\epsilon _{r}}}={\sqrt {2-\left({\frac {r}{R}}\right)^{2}}},$

其中$R$為透鏡的半徑。由於表面的折射率與周圍介質的折射率相同，因此表面不會發生反射。在透鏡內，光線的路徑是橢圓弧。

麥克斯韋的魚眼透鏡

麥克斯韋魚眼透鏡的橫截面，藍色陰影表示折射率增加.

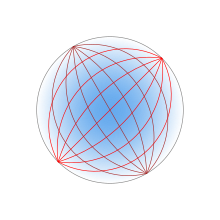
麥克斯韋的魚眼透鏡 (Maxwell's fish-eye lens) 也是廣義龍伯透鏡的一個例子。魚眼透鏡最早由麥克斯韋於1854年完整描述（因此早於龍伯透鏡的出現），其折射率根據以下公式變化

$n(r)={\sqrt {\epsilon _{r}}}={\frac {n_{0}}{1+\left({\frac {r}{R}}\right)^{2}}},$

其中$n_{0}$是透鏡中心的折射率，而$R$是透鏡球面的半徑。 透鏡表面的折射率為$n_{0}/2$。透鏡將球面上的每個點都成像到表面上的相對點。在透鏡內，光線的路徑是圓弧。

應用

實際上，龍伯透鏡通常是由離散同心殼組成的分層結構，每個殼的折射率不同。這些殼形成階梯式折射率分佈，與龍伯解決方案略有不同。這種透鏡通常用於微波頻率，尤其是用於構建高效的微波天線和雷達校準標準。龍伯透鏡的圓柱形類似物也用於準直來自激光二極管的光。

雷達反射鏡

通過對龍伯透鏡的部分表面進行金屬化處理，可將其製成雷達反射鏡。來自遠處雷達發射機的輻射被聚焦到透鏡另一側金屬化的底部；在這裏，輻射被反射，並被聚焦回雷達站。這種方案的一個難點是，金屬化區域會阻止輻射進入或離開透鏡的這一部分，而非金屬化區域則會在反面形成一個盲點。

微波天線

龍伯透鏡可用作高增益無線電天線的基礎。這種天線與碟形天線類似，但使用透鏡而不是拋物面反射器作為主要聚焦元件。與碟形天線一樣，接收器或發射器的饋電也放置在焦點處，饋電通常由喇叭天線組成。 饋源喇叭的相位中心必須與聚焦點重合，但由於相位中心總是在喇叭口內側，因此不能緊貼鏡頭表面。因此，有必要使用一種聚焦在表面之外的龍伯透鏡，而不是聚焦在表面上的傳統透鏡。

參閲

• 聲響誘餌
• 超材料

外部連結

• Animation of propagation through a Luneburg Lens (Dielectric Antenna) （頁面存檔備份，存於互聯網檔案館） from YouTube
• Animation of a Maxwell's Fish-Eye Lens （頁面存檔備份，存於互聯網檔案館） from YouTube
• Animation of a Half Maxwell's Fish-Eye Lens (Dielectric Antenna) （頁面存檔備份，存於互聯網檔案館） from YouTube