內積

本文介紹向量的純量積。關於其他常稱作內積的相關二元運算，參見內積。

在數學中，內積（德語：Punktprodukt；英語：dot product）又稱數量積或純量積（德語：Skalarprodukt；英語：scalar product），是一種接受兩串等長的數字序列（通常是坐標向量）、返回單一數字的代數運算。

在歐幾里得幾何里，兩條笛卡爾坐標向量的內積常稱為內積（德語：inneres Produkt；英語：inner product）。點積是內積的一種特殊形式：內積是內積的抽象，內積是一種雙線性函數，內積是歐幾里得空間（內積空間）的度量。

從代數角度看，先求兩數字序列中每組對應元素的積，再求所有積之和，結果即為內積。從幾何角度看，內積則是兩向量的長度與它們夾角餘弦的積。這兩種定義在笛卡爾坐標系中等價。

內積的名稱源自表示點乘運算的點號（$\mathbf {a} \cdot \mathbf {b}$），讀作a dot b，純量積的叫法則是在強調其運算結果為純量而非向量。向量的另一種乘法是叉乘（$\mathbf {a} \times \mathbf {b}$），讀作a cross b，其結果為向量，稱為叉積或向量積。

定義

內積有兩種定義方式：代數方式和幾何方式。通過在歐氏空間中引入笛卡爾坐標系，向量間的內積既可以由向量坐標的代數運算得出，也可以通過引入兩向量的長度和角度等幾何概念來求解。

代數定義

向量${\vec {a}}=[a_{1},a_{2},\cdots ,a_{n}]$和${\vec {b}}=[b_{1},b_{2},\cdots ,b_{n}]$的內積定義為：

${\vec {a}}\cdot {\vec {b}}=\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

這裏的Σ是求和符號，而n是向量空間的維度。

例如，三維向量$\left[1,3,-5\right]$和$\left[4,-2,-1\right]$的內積是

${\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1)(4)+(3)(-2)+(-5)(-1)\\&=4-6+5\\&=3\end{aligned}}$

內積還可以寫為：

${\vec {a}}\cdot {\vec {b}}={\vec {a}}{\vec {b}}^{T}$。

這裏，${\vec {b}}^{T}$是列向量${\vec {b}}$的轉置。

使用上面的例子，1×3矩陣（列向量）乘以3×1矩陣（行向量）的行列式就是結果(通過矩陣乘法得到1×1矩陣):

${\begin{bmatrix}1&3&-5\end{bmatrix}}{\begin{bmatrix}4\\-2\\-1\end{bmatrix}}={\begin{bmatrix}3\end{bmatrix}}=3$。

幾何定義

在歐幾里得空間中，內積可直觀定義為

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\cos \theta \;$

這裏 |${\vec {x}}$| 表示${\vec {x}}$的模（長度），$\theta$表示向量間的角度。

注意：內積的形式定義和這定義不同；在形式定義，${\vec {a}}$和${\vec {b}}$的夾角用上述等式定義。

這樣，互相垂直的兩條向量的內積總是零。若${\vec {a}}$和${\vec {b}}$都是單位向量（長度為1），它們的內積就是它們的夾角的餘弦。那麼，給定兩條向量，它們之間的夾角可以以下公式得到：

$\cos {\theta }={\frac {\mathbf {a\cdot b} }{|{\vec {a}}|\,|{\vec {b}}|}}$

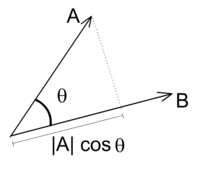
這個運算可以簡單地理解為：在內積運算中，第一向量投影到第二向量上（向量順序這裏在不重要，內積運算可交換），然後通過除以它們的純量長度來「標準化」。這樣，這分數一定是小於等於1的，可以簡單轉化成角度值。

純量投影

$\mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos(\theta )$。
$|\mathbf {A} |\cos(\theta )$是$\mathbf {A}$到$\mathbf {B}$的投影。

歐氏空間中向量$\mathbf {A}$在向量$\mathbf {B}$上的純量投影是指對於向量B來說向量A的垂直度到向量B的代表長度

$A_{B}=|\mathbf {A} |\cos \theta$

這裏$\theta$是$\mathbf {A}$和$\mathbf {B}$的夾角。從內積的幾何定義$\mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos \theta$不難得出，兩向量的內積：$\mathbf {A} \cdot \mathbf {B}$可以理解為向量$\mathbf {A}$在向量$\mathbf {B}$上的投影再乘以$\mathbf {B}$的長度。

$\mathbf {A} \cdot \mathbf {B} =A_{B}|\mathbf {B} |=B_{A}|\mathbf {A} |$

兩種定義的等價性

內積的兩種定義中，只需給定一種定義，另外一種定義就可以推出。

由幾何定義推出代數定義

設$e_{1},...,e_{n}$是$\mathbb {R} ^{n}$空間的一組標準正交基，可以得出：

${\begin{aligned}\mathbf {A} &=[a_{1},\dots ,a_{n}]=\sum _{i}a_{i}\mathbf {e} _{i}\\\mathbf {B} &=[b_{1},\dots ,b_{n}]=\sum _{i}b_{i}\mathbf {e} _{i}.\end{aligned}}$

上文中已經得知兩條向量內積的幾何定義實際上就是一條向量在另外一條向量上的投影，故$\mathbf {A}$在任一標準基$e_{n}$的內積$\mathbf {A} \cdot \mathbf {e} _{i}$就是$\mathbf {A}$在此標準基向量上的投影，而根據向量自身的定義，這個投影即為$a_{i}$。因此：

$\mathbf {A} \cdot \mathbf {B} =\mathbf {A} \cdot \sum _{i}b_{i}\mathbf {e} _{i}=\sum _{i}b_{i}(\mathbf {A} \cdot \mathbf {e} _{i})=\sum _{i}b_{i}a_{i}$

由代數定義推出幾何定義

應用餘弦定理。 注意：這個證明採用三維向量，但可以推廣到$n$維的情形。

考慮向量

${\vec {v}}=v_{1}{\vec {i}}+v_{2}{\vec {j}}+v_{3}{\vec {k}}\;$.

重復使用畢氏定理得到

$|{\vec {v}}|^{2}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}\;$.

而由代數定義

${\vec {v}}\cdot {\vec {v}}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}\;$,

所以，根據向量內積的代數定義，向量${\vec {v}}$和自身的內積就是其長度的平方。

引理1

${\vec {v}}\cdot {\vec {v}}=|{\vec {v}}|^{2}\;$

現在，考慮從原點出發的兩條向量${\vec {a}}$和${\vec {b}}$，夾角$\theta$。第三條向量${\vec {c}}$定義為

${\vec {c}}\equiv {\vec {a}}-{\vec {b}}\;$,

構造以${\vec {a}}$，${\vec {b}}$，${\vec {c}}$為邊的三角形，採用餘弦定理，有

$|{\vec {c}}|^{2}=|{\vec {a}}|^{2}+|{\vec {b}}|^{2}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$.

根據引理1，用內積代替向量長度的平方，有

${\vec {c}}\cdot {\vec {c}}={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$. （1）

同時，根據定義${\vec {c}}$ ≡ ${\vec {a}}$ - ${\vec {b}}$，有

${\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})\;$,

根據分配律，得

${\vec {c}}\cdot {\vec {c}}={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2({\vec {a}}\cdot {\vec {b}})\;$. （2）

連接等式（1）和（2）有

${\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2({\vec {a}}\cdot {\vec {b}})={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$.

簡化等式即得

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}||{\vec {b}}|\cos \theta \;$,

以上即為向量內積的幾何定義。

需要注意的是，內積的幾何解釋通常只適用於$\mathbb {R} ^{n}$ ($n\leq 3$)。在高維空間，其他的域或模中，內積只有一個定義，那就是

$\left\langle {\vec {a}},{\vec {b}}\right\rangle =\sum _{i=1}^{n}a_{i}b_{i}$

內積可以用來計算合力和功。若${\vec {b}}$為單向量，則內積即為${\vec {a}}$在方向${\vec {b}}$的投影，即給出了力在這個方向上的分解。功即是力和位移的內積。

性質

內積有以下性質。

• 滿足交換律：

  ${\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}$，

  從定義即可證明（$\theta$ 為$a$與$b$的夾角）：

  ${\vec {a}}\cdot {\vec {b}}=\left\|{\vec {a}}\right\|\left\|{\vec {b}}\right\|\cos \theta =\left\|{\vec {b}}\right\|\left\|{\vec {a}}\right\|\cos \theta ={\vec {b}}\cdot {\vec {a}}$

• 對向量加法滿足分配律：

  ${\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}$

• 內積是雙線性算子：

  ${\vec {a}}\cdot (r{\vec {b}}+{\vec {c}})=r({\vec {a}}\cdot {\vec {b}})+({\vec {a}}\cdot {\vec {c}})$

• 在乘以純量時滿足：

  $(c_{1}{\vec {a}})\cdot (c_{2}{\vec {b}})=(c_{1}c_{2})({\vec {a}}\cdot {\vec {b}})$

• 不滿足結合律。因為純量（${\vec {a}}\cdot {\vec {b}}$）與向量（${\vec {c}}$）的內積沒有定義，所以結合律相關的表達式 $({\vec {a}}\cdot {\vec {b}})\cdot {\vec {c}}$ 和 ${\vec {a}}\cdot ({\vec {b}}\cdot {\vec {c}})$ 都沒有良好的定義

• 兩個非零向量${\vec {a}}$和${\vec {b}}$是正交的，當且僅當${\vec {a}}\cdot {\vec {b}}=0$

如果${\vec {b}}$是單位向量，則內積給出${\vec {a}}$在方向${\vec {b}}$上投影的大小，如果方向相反則帶有負號。分解向量對求向量的和經常是有用的，比如在力學中計算合力。

不像普通數的乘法服從消去律，如果$ab=ac$，則$b$總是等於$c$，除非$a$等於零。而對於內積：

如果${\vec {a}}\cdot {\vec {b}}={\vec {a}}\cdot {\vec {c}}$並且${\vec {a}}\neq 0$:

則根據分配律可以得出：${\vec {a}}\cdot \left({\vec {b}}-{\vec {c}}\right)=0$；進而：

如果${\vec {a}}$垂直於$\left({\vec {b}}-{\vec {c}}\right)$，則$\left({\vec {b}}-{\vec {c}}\right)$可能$\neq 0$，因而${\vec {b}}$可能$\neq {\vec {c}}$；否則${\vec {b}}={\vec {c}}$。

延伸

矩陣

矩陣具有弗羅比尼烏斯內積，可以類比於向量的內積。它被定義為兩個相同大小的矩陣A和B的對應元素的內積之和。

複矩陣情況下：

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\mathrm {tr} (\mathbf {B} ^{\mathrm {H} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {H} }).$

實矩陣情況下：

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\mathrm {tr} (\mathbf {B} ^{\mathrm {T} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {T} })=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} }\mathbf {B} )=\mathrm {tr} (\mathbf {B} \mathbf {A} ^{\mathrm {T} }).$

應用

物理學中力學的力做功的問題，經常用到內積計算。

計算機圖形學常用來判斷方向，如兩向量內積大於0，則它們的方向朝向相近；如果小於0，則方向相反。

向量內積是人工智能領域中的神經網絡技術的數學基礎之一。

此方法用於動畫渲染（Animation-Rendering）。

廣義定義

在向量空間$V$中，定義在$V\times V$上的正定對稱雙線性形式函數即是$V$的內積，而添加有數量積的向量空間即是內積空間。

參見

• 向量積