四色定理

四色定理(英語:four color theorem),又稱四色地圖定理(four color map theorem),是一個數學定理[1]:如果在平面上劃出一些鄰接的有限區域,那麼可以用四種顏色來給這些區域染色,使得每兩個鄰接區域染的顏色都不一樣[2][3];另一個通俗的說法是:每個無外飛地的地圖都可以用不多於四種顏色來染色,而且不會有兩個鄰接的區域顏色相同。被稱為鄰接的兩個區域是指它們有一段公共的邊界,而不僅僅是一個公共的交點。例如右圖左下角的圓形中,紅色部分和綠色部分是鄰接的區域,而黃色部分和紅色部分則不是鄰接區域。
「是否只用四種顏色就能為所有地圖染色?」的問題最早是由南非數學家法蘭西斯·古德里在1852年提出的,被稱為「四色問題」或「四色猜想」。人們發現,要證明寬鬆一點的「五色定理」(即「只用五種顏色就能為所有地圖染色」)很容易,但四色問題卻出人意料地異常困難。曾經有許多人發表四色問題的證明或反例,但都被證實是錯誤的。
1976年,數學家凱尼斯·阿佩爾和沃夫岡·哈肯藉助電腦首次得到一個完全的證明,四色問題也終於成為四色定理。這是首個主要藉助電腦證明的定理。這個證明一開始並不為許多數學家接受,因為不少人認為這個證明無法用人手直接驗證。儘管隨着電腦的普及,數學界對電腦輔助證明更能接受,但仍有數學家希望能夠找到更簡潔或不藉助電腦的證明。
嚴格敘述
[編輯]四色定理的通俗版本是:「任意一個無外飛地的地圖都可以用四種顏色染色,使得沒有兩個相鄰國家染的顏色相同。」
作為一個數學定理,四色定理有着更為嚴謹的數學敘述。
拓撲學闡述
[編輯]最初的染色問題是用幾何學的概念描述的,嚴謹的版本則需要用到拓撲學的概念來定義。設有一平面或其一部分,將其劃分為互不重疊的區域的集合。一個「地圖」為以下劃分方式[2]:44:
所謂有界區域,是指能夠用一個長和寬都有限的矩形覆蓋的區域。無界區域則是不能用這樣的矩形覆蓋的區域[2]:44。每個區域相當於通俗說法中的「國家」,而區域之間的邊界(「國家」之間的「國界線」)則定義為連續不自交的曲線,也稱為連續簡單曲線。連續簡單曲線是指一個從[0, 1]對映到平面的連續函數的像集:,並且要滿足:
- 任意,只要不是,就必定有
這樣說明曲線不與自身相交(沒有「打結」的地方)。如果,就稱曲線為弧,否則稱曲線為圈[2]:47。可以看出,用邊界定義地圖更為本質:
平面中的一張地圖是指有限個簡單曲線的集合:,其中,為[0, 1]對映到的連續函數。並且任意,曲線和要麼沒有交點(交集為空集),要麼交點是兩線的一個公共頂點[2]:60
中每一條連續簡單曲線稱為地圖的邊。任意邊的端點稱為頂點。可以說,一張地圖實際上是由一個簡單有界平面圖定義的。定義地圖的邊和頂點後,設所有屬於邊或頂點的點為中性點,其集合設為,則 將其餘的點劃分為若干個路徑連通的開集。用拓撲學的語言來說,每個「國家」是的一個極大連通子集。或者說,取一個非中性點,所有能夠從,經過一條不含中性點的弧到達的點構成的集合,就是一個國家。這樣定義的國家必然滿足之前所說的特性,只有一個無界國家。要注意的是這裏定義的國家必然是沒有飛地的[2]:64。
最後可以定義染色。假設將使用到的顏色編號為號顏色,為地圖染色是指一個將地圖中的國家對映到上的函數。一個可行的n-染色方案是指使得相鄰的國家對應的顏色不同的函數。四色定理說明:每個地圖都存在可行的4-染色方案[2]:43。
圖論闡述
[編輯]拓撲學版本的四色問題闡述可以轉化為更為抽象的圖論版本。這裏的轉化指的是一種對偶的概念。即將一個地圖轉化為圖論中的一個無向平面圖。具體來說,是將地圖中的每一個國家用其內部的一個點代表,作為一個頂點。如果兩個國家相鄰,就在兩個頂點之間連一條線。這樣得到的圖必然是一個平面圖(不會有兩條邊相交),而與每個國家選取的代表點無關。四色定理可以敘述為:必然可以用四種顏色給平面圖的頂點染色,使得相連的頂點顏色不同[2]:118-122。
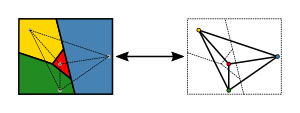
要注意的是,並非所有的地圖都可以轉化為圖論中的平面圖。如果一個國家有飛地的話,就不能用只一個點來代表一個國家。另外,如果一個國家是「國中國」,那麼即便可以地圖其轉化為平面圖,也會造成討論上的不便。但是,「國中國」的着色十分容易解決,因為它只有一個鄰國,只需將它染成和鄰國不一樣的顏色就可以。所以在大部分有關四色問題的討論中可以忽略「國中國」的情形。同樣地,只有兩個鄰國的情形也可以被忽略。如果規定不能夠有四個或者以上的國家有公共邊界,那麼地圖轉化成的平面圖裏面,每個區域都是至多由三條邊圍成的。這樣的地圖被稱為正規地圖。如果任何一個頂點都連出三條邊,那麼就稱其為「三度圖」(trivalent map)。可以證明,如果存在四色定理的反例,那麼國家數最少的反例必定是三度圖。因此在四色問題的證明過程中,常常會假設地圖對應的圖是三度圖[2]:127-128。
問題的提出
[編輯]
「只需要四種顏色為地圖着色」最初是由法蘭西斯·古德里在1852年提出的猜想。法蘭西斯·古德里於1831年生於倫敦。1850年,他在倫敦大學學院完成他的數學學士學位後,又花兩年時間修得法學學士學位[2]:2-3。1852年,古德里在繪製英格蘭分郡地圖時,發現許多地圖都只需用四種顏色染色,就能保證有相鄰邊界的分區顏色不同。他將這個發現告訴他的弟弟弗雷德里克·古德里[4]:92。弗雷德里克這時正在倫敦大學學院讀數學,師從法蘭西斯上學時的老師奧古斯塔斯·德摩根[2]:2,5。10月23日,弗雷德里克將他哥哥的發現作為一個猜想向老師德摩根提出。德摩根對此猜想很感興趣,在同一天就在通訊中將這個問題向愛爾蘭數學家威廉·哈密頓提出。德摩根的信如今仍然儲存在都柏林三一學院中[2]:7。與德摩根的熱情相反,哈密頓對這個問題絲毫不感興趣。他在三天後的回信中告訴德摩根,他「不會嘗試解決這個四元顏色問題」[2]:5。

四色問題之所以能夠得到數學界的關注,德摩根功不可沒。他推動四色問題研究的工作如此盡力,以至於許多人認為德摩根才是首先提出這個猜想的人。德摩根在接下來的兩年裏又嘗試向別的數學家通訊。他在1853年12月9日與1854年6月24日分別寫信給他以前的老師威廉·魏巍爾以及魏巍爾的妹夫羅伯特·萊斯利·艾里斯,討論四色問題。1860年4月14日,德摩根在《雅典娜雜誌》上發表對魏巍爾新書的書評,其中再次提到四色定理。1854年古德里兄弟中的一人也曾在同一本雜誌上發表過四色定理的文章[2]:11。儘管德摩根的書評直到1876年才引起大規模的注意,但從其發表開始,已經有了一定影響。美國邏輯學家、哲學家查爾斯·桑德斯·皮爾斯看到雜誌上的文章後,便向哈佛大學數學學會投遞了一份嘗試性證明(非真正證明),對可能的證明思路進行了一定探討[5]。
肯普的證明
[編輯]1878年6月13日,在倫敦王家數學學會的一次會議上,阿瑟·凱萊向其他與會者詢問,四色足夠為地圖着色的問題是否已經被證明。不久之後,他就此問題寫了一篇短小的論文,對問題作了簡要介紹和分析,投給英國王家地理學會,並於次年(1879年)在學會會刊上發表[2]:13。凱萊的文章使得四色定理重新進入到數學家們的視野中。這一次,四色定理引起更多的注意。凱萊的論文發表尚不到一年,一份「可能是最有名的四色問題的錯誤證明」就出現了[2]:15[4]:94。

作出這個證明的人是倫敦律師兼數學家阿爾弗雷德·布雷·肯普。肯普曾是凱萊在劍橋大學的學生,之前因為在聯動裝置模型方面的工作而出名。《自然》雜誌首先確認了他的證明,於1879年7月17日登載「四色猜想得到證明」的訊息。完整的證明很快在當時剛剛成立不到兩年,尚未出名的《美國數學雜誌》上發表[6]。其中原因主要是創辦《美國數學雜誌》的詹姆斯·約瑟夫·西爾維斯特是凱萊的好友,因此肯普「應雜誌主編要求」,將這篇很有分量的論文發表在相對不知名的雜誌上[2]:15。
《美國數學雜誌》的顧問編輯威廉·愛德華·斯多利對這個問題也很感興趣[7]。他對肯普的證明做了一些簡化,並加上多個肯普未曾處理的特殊情況下的證明,收錄在再版時的附錄里。1879年11月5日,在約翰·霍普金斯大學科學協會的一次會議上,這個最終版本的證明首次公開。皮爾斯當時也在約翰·霍普金斯大學任教,他也出席了這次會議,並提出自己以前的工作,又在12月的另一次會議中提出他使用邏輯方法對證明作出的改進[2]:16。至此,數學界認為四色猜想已經被完全解決[2]:16[4]:102。
1880年,物理學家彼得·古德里·泰特也在《愛丁堡皇家學會會刊》發表一個四色猜想的新證明,然而其中只是將四色問題進行了一定的變形,依賴於肯普的工作,並沒有實質的證明[2]:20。
肯普的證明思路
[編輯]肯普的證明是基於對國家數目進行的歸納法。很容易能證明國家數4以內時四色定理成立。肯普假設當國家數目不多於n時四色定理成立,他的目的是證明n+1個國家構成的地圖都可以約化為不超過n個國家構成的地圖,從而證明四色定理成立[6][8]。

肯普首先證明一個有關平面圖的結論:任意地圖中必定存在一個國家(頂點),其鄰國數目小於等於5。證明很簡單,在圖論版本中,地圖被轉換成簡單平面圖。而一個簡單平面圖中,設V為頂點數,E為邊數,F為區域數,則由於每個區域至少由三條邊圍成,每條邊正好隔開兩個區域,所以區域數和邊數滿足:2E ≥ 3F。假設每個頂點都至少有6條邊,那麼由於每條邊對應兩個頂點,所以頂點數和邊數滿足:2E ≥ 6V。合起來就有:
但這與圖論中著名的歐拉公式:V + F = E + 2矛盾。因此不可能每個頂點都至少有六條邊,也就是說,必定有一個國家的鄰國數目不超過5[3]:177。
接下來肯普考察n+1個國家中鄰國數目最小的國家,稱之為A國。A國鄰國的數目不超過5個。如果A國的鄰國數目不超過3個,那麼可以把A國「去掉」(比如和其中一個鄰國連成一體),形成一個n個國家的地圖,這個地圖可以用4種顏色着色,而原來的3個鄰國至多用了3種顏色。這時候將A國「放回去」,染上第4種顏色,就等於找到給原地圖4-着色的方法[8]。
這種能夠「去掉」一個國家,減少國家數的局部後來被稱為「可約構形」(reducible configuration)。接下來肯普證明A國有4個鄰國和5個鄰國的情況仍然是可約構形,於是都能夠化為不多於n個國家的情況。因此任何n+1個國家的地圖仍然可以用四種顏色染色,因而通過歸納法可知,四色定理成立[6]。
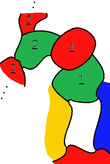
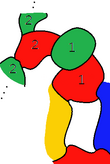
A國有4個鄰國的時候,假如有兩個鄰國同色,那麼可以把它們「當作」同一個國家,和A國連成一體進行約化,而由於此時這4個鄰國至多用了3種顏色,所以可以將A國「放回去」,染上第4種顏色。假如4個鄰國都不同色,不妨設為紅、黃、藍、綠(如右圖1)。肯普的思路是將其轉化為兩個鄰國同色的情形,他採用的方法後來被稱為「肯普鏈」方法(Kempe chain)。具體來說,肯普希望將其中一個鄰國的顏色換成「對面」的顏色,比如將綠色(圖1中的綠1)換為紅色。如果綠色鄰國沒有紅色的鄰國,那麼換色沒有任何問題;如果它有紅色鄰國(圖1中的紅1),那麼需要將其紅色換成綠色,……如此換下去。因此需要換色的是一條綠-紅-綠-紅……的「鏈條」,也就是所謂的「肯普鏈」。如果對面的紅色國家不在這個鏈條里,那麼只需要將鏈中的國家紅綠互換,就能轉化成兩個鄰國同色的情況(圖2)。如果對面的紅色國家也在鏈條裏面(如圖3),那麼紅綠互換就沒有意義了。但是這時候可以看到,紅綠「肯普鏈」與A國形成一個圈,所以黃色鄰國和藍色鄰國必有一個在圈裏(圖3中是黃色鄰國)。這樣圈外的(藍色)鄰國的「肯普鏈」與圈內的(黃色)鄰國必定沒有交集,於是將其黃藍互換,就能轉化成兩個鄰國同色的情況。這說明A國與4個鄰國構成可約構形[3]:178[6]。
對於A國有5個鄰國的構形,肯普仍然使用肯普鏈的換色方式來證明其可約性。他使用了兩次換色,將5種顏色降至3種,從而成為可約的構形,如果A國的5個鄰國只用了3種顏色,就可以將A國放回去,染上第4種顏色。如果A國的5個鄰國用了4種顏色,不失一般性,假設依照順時針方向為紅、黃、紅、藍、綠,則先嘗試由藍色鄰國開始將其藍黃互換,如果對面的黃色國家沒有在鏈條裏面,就能把A國染上藍色,如果對面的黃色國家在鏈條裏面(那麼藍黃互換就沒有意義了),就嘗試從綠色鄰國開始將其綠黃互換,如果對面的黃色國家沒有在鏈條裏面,就能把A國染上綠色,如果對面的黃色國家又在鏈條裏面(那麼綠黃互換就沒有意義了),則從黃色鄰國和藍色鄰國中間的紅色鄰國開始將其紅綠互換(對面的綠色鄰國一定不會在鏈條裏面),再從黃色鄰國和綠色鄰國中間的紅色鄰國開始將其紅藍互換(對面的藍色鄰國一定不會在鏈條裏面),然後把A國染上紅色。這也是後來希伍德找出錯誤的地方[6][8]。
無法修正的錯誤
[編輯]四色猜想在短短的兩年時間裏被一個並非「專業」數學家的「外行人」解決,讓很多當初認為這個問題是難題的數學家覺得,這個問題也許並沒有涉及到數學中深層的本質難點。對四色問題的研究逐漸減少,數學家們已經將其視為事實。劉易斯·卡羅爾將四色問題化為遊戲:一方設計地圖,另一方來為其着色[9]。1886年,英國男校克里夫頓學院校長將四色問題作為給全校學生挑戰的難題,要求答案長度「不得超過一頁紙的文字,30行算式以及一頁紙的圖」[4]:105。
德國數學家菲利克斯·克萊因甚至將這個問題和1840年莫比烏斯提出並解決的另一個問題相混淆起來,認為四色問題不過是後者的直接推論。這個誤解被幾何學家理查德·巴爾策在1885年重複,導致直到21世紀仍有類似的傳言[2]:21。而實際上莫比烏斯解決的是完全圖不是平面圖的問題,與四色問題沒有直接關係。
然而,在肯普的證明發表的11年之後,珀西·約翰·希伍德發表一篇文章,指出肯普的證明中包含一個錯誤。希伍德在文章中遺憾地指出,他無法修正這個錯誤,以得到一個四色問題的正確證明,因此他的文章更多是摧毀而非建設(rather destructive than constructive)[2]:22。不過,儘管無法得到四色定理,希伍德仍然在肯普的思路上前進,得到一個較弱的定理:五色定理。
根據希伍德的說明,肯普的錯誤在於證明5鄰國是可約構形時,構造兩條肯普鏈以換色,然而第二次換色時,肯普的方法並不總是成功的。希伍德提供一個包含25個國家的地圖作為反例[4]:106。
希伍德的報告是由肯普自己提交給倫敦皇家數學學會的。肯普承認自己的證明中存在缺陷,並且他未能去除這個缺陷[4]:107。然而希伍德的工作並沒有受到應有的重視。數學界普遍認為這只是無關緊要的錯誤,很快就能得到糾正。1894年創刊的《L'intermédiaire des mathématiciens》雜誌以四色問題作為頭一個徵解問題,結果很快就收到解答,稱其已被解決,並參照了肯普、泰特等人的論文。E.呂卡的《娛樂數學》(Récréations mathématiques)第四卷提到肯普的證明,但絲毫沒提到希伍德已經指出肯普證明的錯處[4]:108[10]。
直到世紀之交時,數學家們仍舊認為,四色問題所需要的只是某個靈光一現的妙想。一個廣為流傳的故事是閔可夫斯基在教拓撲學課時提到四色問題,說:「這個問題一直沒有解決,只是因為試圖解決它的都是三流的數學家」。他聲稱要在課上證明之,但直到下課仍然無法成功,在耗費若干堂課的時間後,只能承認失敗[11]:92。
從歐洲到美國
[編輯]20世紀起,歐洲數學界對四色定理的研究出現停滯。相反地,這個問題在美國得到更多的關注。不少傑出的數學家研究了這個問題,並作出很大貢獻。一部分的努力是修正肯普的證明;另一方面的努力是延續泰特的思路,將四色問題進行轉化,以使用更多有力的數學工具。
對四色問題的轉化在泰特之後並未停止過。從拓撲學的版本轉化至圖染色的版本後,希伍德又在1898年提出新的變形。肯普和泰特已經注意到,證明四色問題只需要考慮三個國家有共同「交點」的情況,更多國家有共同交點的情形可以轉化為前者。因此這樣對應的染色圖中,每個頂點恰會連出三條邊。這樣的圖被稱為「三度圖」(trivalent map)。希伍德觀察到,如果三度圖中任意由邊圍成的區域,邊的個數都是3的倍數,那麼圖可以被4-染色。他進一步發現,只要存在一種給圖的頂點賦值+1或-1的方法,使得每個區域的頂點數字之和都被3整除,那麼圖可以被4-染色。可以證明,4-染色和存在賦值方法是等價的[4]:159。

在美國,數學家對四色定理的研究從未停止過。除了約翰·霍普金斯大學的皮爾斯以及斯多利等人外,另一個研究者是保羅·溫尼克。從當時的學術聖地哥廷根大學畢業的溫尼克來到美國後在肯塔基大學任教。他1904年發表的論文中已經出現了可約性的雛形。然而美國數學界在四色問題上首次實質性的進展出現在1912年後。普林斯頓大學的奧斯瓦爾德·維布倫(經濟學家托爾斯坦·范伯倫的侄子)是這波浪潮的先鋒。他的工作重心是拓撲學,1905年證明了若爾當曲線定理[12]。對龐加萊發展出的新代數工具有深入了解的他,很自然地開始對四色定理的研究。他使用有限幾何學的觀念和有限體上的關聯矩陣作為工具[4]:160,將四色問題轉化成有限體系數空間上的方程問題。這個方向被後來的密碼學家、數學家威廉·托馬斯·塔特稱為「量化方法」(the quantitative method)。同年,他的普林斯頓同僚喬治·戴維·伯克霍夫也開始探索這個方向,但一年之後他開始轉向肯普的方法,也即是塔特所稱的「定性方法」(the qualitative method),並提出可約環(reducible ring)的概念[2]:25。1913年,伯克霍夫發表名為《地圖的可約性》(The Reducibility of Maps)的論文,利用可約環證明了:由不超過12個國家構成的地圖都能用四色染色。1922年,伯克霍夫的學生菲利普·富蘭克林運用同樣的方法,將結論加強到:不超過25個國家構成的地圖都能用四色染色[4]:160[13][14]。由於別克霍夫首次證明四色定理對不超過12個國家的地圖成立,歷史上證明的可染色地圖的國家數上限記錄被稱為別克霍夫數[4]:167。
不可避免的可約構形集
[編輯]伯克霍夫等人的證明是肯普的方法的延續和系統化,歸納為尋找一個不可避免的可約構形集(an unavoidable set of reducible configurations)。這個理念已經體現在肯普的證明中。他首先說明任一地圖中必然存在以下四種構形:2鄰國國家、3鄰國國家、4鄰國國家和5鄰國國家;然後證明每種構形都是可約構形。後來希爾將這種分類方式稱為「不可避免集」。伯克霍夫的構想是使用反證法:反設存在至少需要五種顏色染色的地圖,那麼其中必然存在國家數最小的「極小五色地圖」(five-chromatic map)。這個地圖必然是「不可約的」(irreducible)。而只要找到一組構形,使極小五色地圖中不可避免地會出現其中一種構形,並且每個構形都是可約的,那麼就能夠通過約化,將地圖的國家數減少,從而導致矛盾[4]:169。


肯普找的不可避免集由四種構形組成,但他無法證明最後一種(5鄰國國家)的可約性,因此伯克霍夫開始尋找刻畫不可避免集的新方法。他提出以相鄰國家連成的環來將整個地圖M分為三個部分:環內部分A、環外部分B以及環本身R。若環上的國家數為n就稱其為n-環。如果R的任意染色都不妨礙A進行染色,那麼就可以「忽略」A而將M的染色問題約化為B+R的染色問題。這時便稱A+R是可約構形,R稱為可約環。伯克霍夫證明了:當R是4-環,或者R是5-環且A中國家不止一個,或者A+R是「伯克霍夫菱形」時,A+R都是可約的構形。因此極小五色地圖不可能包含這些構形[4]:169。富蘭克林進一步證明:極小五色地圖中必定包含三個鄰接的五邊國(5鄰國的國家),或者鄰接的兩個五邊國與一個六邊國,或者鄰接的一個五邊國和兩個六邊國。他從而得出一系列的可約構形,形成了25國以下地圖的不可避免的可約構形集。因此推出,極小五色地圖必定至少包含26個國家[14]。
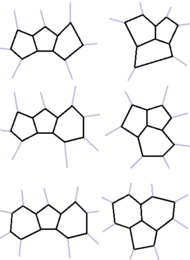
這種方法的終極目標是找到所有地圖的不可避免的可約構形集。然而隨着國家數增多,要找到不可避免集並證明其可約化性就越難。這主要是因為隨着環的增大,染色的方法數目會迅速增大。6-環的4-染色方法有31種,而12-環則有22144種。因此對大環圍成的構形驗證可約性是十分繁雜的工作。1926年,C.N.Reynolds將別克霍夫數從25提高到27。1938年,富蘭克林將其推進到31。1941年,C.E.Winn將之提高到35。而直到1968年,別克霍夫數才更新為40[2]:185。
四色問題研究的下一個突破並不是在美國,而是由哥廷頓大學出身的德國數學家亨利·希爾帶來的。他在1948年提出不可避免集的存在性,但他提出的不可避免集可能包含10000個構形,其中還有18-環的龐大構形。希爾的另一個成果是在1969年提出「放電法」(discharging method),為尋找不可避免集給出了系統的方法[3]:188。
放電法
[編輯]放電法利用地圖轉換成圖染色後成為平面圖的特性,將其看作是平面的「電網」,並將每個「節點」按照度數(連出的邊數)分類。首先在每個度數為k的節點放置6 - k的電荷。根據平面圖和極小五色地圖的特性,有下列恆等式[2]:224:
其中表示度數為k的節點個數,s為節點最大度數。「放電」的過程(discharging procedure)指的是將這些電荷以特殊的規則進行重新分配,從而找出「電網」結構上的特性,建立不可避免集。具體來說,可以假設某些構形全不存在,然後構造一個放電過程,使得接受電荷的總量不再等於釋放電荷的總量,從而匯出矛盾(電荷不守恆)。每個良好設計的放電過程都能證明一個不可避免集的存在[3]:189-192[15]:26-27。
電腦的輔助
[編輯]人工尋找不可避免構形集和驗證構形可約性過於緩慢,數學家開始考慮使用當時新出現的電腦作為輔助,以提高驗證的效率。構造出放電法的同時,藉助於電腦來驗證構形可約性的工作也飛速進展。希爾在Karl Dürre的幫助下在1965年設計了第一個演算法來驗證構形的可約性。他們使用的是Algol 60語言,在德國漢諾威技術學院電腦中心的一台CDC 1504A電腦上首次執行。1967年前,由於主記憶體不足,只能驗證12-環以下的構形[2]:27。而希爾找出的不可避免集含有的大構形可以達到14-環甚至更多,電腦的能力並不足以快速完成可約性的驗證[16]。
當時美國的電腦技術領先於歐洲,因此希爾希望能夠藉助美國的大型電腦來證明四色定理。1967年,美國紐約布魯克海文國家實驗室(BNL)應用數學院院長邀請希爾來美國訪問,並允許他使用當時世界上最快的電腦CDC 6600。其後幾年,希爾兩度到美國尋求大型電腦的使用機會。這段時間中,Dürre將程式用FORTRAN進行重寫。抱着在德國最終解決四色問題的希望,希爾回到德國,但令他失望的是,德國學術界對他的計劃持否定態度,並不願為他的程式撥出計算時間[2]:28。
在數次訪美時,希爾開始與沃夫岡·哈肯合作。哈肯在1948年曾經旁聽過希爾提出不可避免集的課程,之後對四色定理產生了持續的興趣。兩人通過信件交流合力作出很多進展,為最終解決四色問題鋪平道路。1971年,阿佩爾也開始在哈肯的介紹下研究四色問題。然而當時哈肯對解決四色問題的前途感到悲觀,因為尋找並驗證合適的不可避免可約構形集實在過於複雜,即便藉助電腦也需要過多的時間。塔特當時也認為,即便最樂觀的估計中,不可避免集也要包含至少8000個構形。然而塔特等人也將希爾的工作介紹到美國(當時希爾的工作只在德國發表過),並引發了很多人的熱情。包括弗蘭科·阿萊爾、愛德華·雷尼爾·斯瓦特、弗蘭科·R·伯恩哈特等人都開始尋找不可避免集以及檢驗可約性[2]:34。哈肯和阿佩爾依賴於電腦的工作能力,因此不斷改良放電過程。他們將通過放電過程尋找不可避免集的演算法和驗證可約性結合起來,當某個不可避免集的構形不是C-可約(可約性的一種)或難以被驗證為C-可約的時候,就放棄這個不可避免集,以提高效率。兩人設定了很多經驗性的修正規則,比如設定三個經驗性的「障礙」(三種特定的構形),當某個構形中含有這種障礙就直接認為是不可約的;又比如構形的大小不能超過14-環,等等[3]:193。
定理的證明
[編輯]1975年,哈肯找到一種很好的放電過程,但難以化為演算法程式。於是兩人暫時開始迴歸紙筆計算。這時候他們得到當時還是博士學生的約翰·科赫(John A. Koch)的支援,後者對他們提供了可約性驗證演算法工作上的幫助。1976年3月,他們終於得到一個由1936個構形組成的不可避免集,對應的放電過程由487條規則構成[17]:26。同時伊利諾伊大學的主電腦也更換成運算速度更高的IBM 360,為計算節省大量時間。經過電腦1200小時的驗證,他們終於在6月得出:1936個構形都是可約構形。這代表着四色定理最終的解決[2]:35。這時候他們的幾個競爭對手如阿萊爾、斯瓦特等的工作也將近尾聲。
1976年6月22日,哈肯和阿佩爾首次在美國數學協會(M.A.A.)於多倫多大學召開的美國數學學會(A.M.S.)夏季會議公佈他們的結果。不久,伊利諾伊大學數學系的郵戳上加上了「四種顏色就夠了」(FOUR COLORS SUFFICE)的一句話,以慶祝四色猜想得到解決[17]:24[18]。9月,美國數學學會的公告專欄上刊登了兩人證明四色定理的訊息[19]。
1977年,哈肯和阿佩爾將結果寫成名為《任何平面地圖都能用四種顏色染色》(Every planar map is four colorable)的論文,分成上下兩部分,發表在《伊利諾伊數學雜誌》(Illinois Journal of Mathematics)上[20][21]。
爭議、修正與改良
[編輯]四色定理是第一個主要由電腦驗證成立的著名數學定理。這一證明剛開始並不被所有的數學家接受。1979年,邏輯哲學和數學哲學家托馬斯·蒂莫茲佐在《四色定理及其哲學意義》一文中提出,四色定理與其證明能否稱之為「定理」和「證明」,尚有疑問。「證明」的定義也需要進行再次審視。蒂莫茲佐的理由包括兩點:一方面,電腦輔助下的證明無法由人力進行核查審閱,因為人無法重複電腦的所有運算步驟;另一方面,電腦輔助的證明無法形成邏輯上正則化的表述,因為其中的機器部分依賴於現實經驗的反饋,無法轉換為抽象的邏輯過程[22][23]。即便在數學界中,對四色定理證明的誤解也存在着。有的數學家認為證明是傑出的進展,也有人認為依賴電腦給出的證明很難令人滿意[3]:197。也有人認為,電腦輔助證明數學定理不過是對人的能力進行延伸的結果,因為電腦不過是依照人的邏輯來進行每一步的操作,實際上只是將人能夠完成的工作用更短的時間來完成[3]:198。還有人將電腦輔助證明和傳統證明的差別比喻為藉助天文望遠鏡發現新星和用肉眼發現新星的區別[24]。
針對證明過程冗長、難以理解的問題,哈肯等人也着手對證明進行改良。簡化證明的一個方向是尋找更小的不可避免集和更加容易驗證的可約構形。哈肯等人很快將不可避免構形集的大小從1936個改進到1476個。1994年,羅賓·托馬斯等人又將其改進到只包含633個構形、32個放電規則的放電過程推出的不可避免構形集[25]。由於著名的前車之鑑,數學家們對證明進行詳細審視,發現了大量缺漏和錯誤。特別是厄里奇·史密德等人曾經檢查人工證明部分的40%,並發現放電過程中的一個關鍵性錯誤。幸好,這些缺陷和錯誤都是能夠修正的。不過,修正的工作也持續了若干年,才最終完成[2]:36。修正過程中也出現各種傳言,說四色定理的證明其實是錯誤的。1986年,哈肯和阿佩爾應《數學情報》雜誌的邀請寫了一篇短文,用清晰易懂的語言總結他們的證明工作[2]:35。1989年,最終的定稿以單行本的形式出版,超過400頁[26]。
對於機器證明的可靠性問題,2004年9月,數學家喬治·龔提爾使用證明驗證程式Coq來對當時交由電腦運算的演算法程式進行形式上的可靠性驗證。證明驗證程式是一個由法國開發的軟件,能夠從邏輯上驗證一段電腦程式是否正常執行,並且是否達到了它應該達到的邏輯目的。驗證表明,四色定理的機器驗證程式確實有效地驗證所有構形的可約性,完成了證明中的要求。至此,除了機器硬件、軟件可能存在問題外,四色定理的理論部分和電腦證明演算法部分都得到驗證[27]。
儘管絕大多數數學家對四色定理的證明已經不再有疑問,某些數學家對經由電腦輔助的證明方式仍舊不夠滿意,希望能找到一個完全「人工」的證明。正如湯米·R·延森和比雅尼·托夫特在《圖染色問題》一書中問的:「是否存在四色定理的一個簡短證明,……使得一個合格的數學家能在(比如說)兩個星期裏驗證其正確性呢[3]:199?」
實際應用
[編輯]
雖然四色定理證明任何地圖可以只用四個顏色着色,但是這個結論對於現實上的應用卻相當有限。據凱尼斯·梅所言:「(實際中)用四種顏色着色的地圖是不多見的,而且這些地圖往往最少只需要三種顏色來染色。地圖學和地圖製圖史相關的書籍也沒有四色定理的記載[26]。」現實中的地圖常會出現飛地,即兩個不連通的區域屬於同一個國家的情況(例如美國的阿拉斯加州),而製作地圖時仍會要求這兩個區域被塗上同樣的顏色。此外,即便地圖能夠只用四種顏色染色,為了區分起見,也會採用更多的顏色,以提示不同地區的差別[28]:63。
染色演算法
[編輯]地圖染色演算法是一個應用的問題:能否給出一個演算法,將一個地圖進行k-染色,或判定它不能k-染色?當k = 2時,存在多項式時間的演算法。只需將某個國家隨機染上一種顏色,然後它的鄰國就只能染成另一種顏色,鄰國的鄰國的顏色也隨之確定……這個演算法等價於廣度優先搜尋,因此是多項式時間的。當k = 3時,可以證明這個問題是NP完備的,即若P≠NP,則不存在多項式時間的演算法[29]:583。對於k = 4的情況,阿佩爾和哈肯在1989年的單行本的附錄中給出一個完整的多項式時間的演算法及其證明[26]。
曲面地圖染色
[編輯]

四色問題探討的是平面上地圖的染色問題。更一般的情況:曲面上地圖的染色問題是由希伍德開始研究的。他在1890年的論文中不僅指出肯普的錯誤,而且運用肯普的方法證明了五色定理。在此之後,希伍德又將注意力轉移到更一般的曲面染色問題上。他證明能夠對Sk上面任何的地圖進行染色,使得相鄰兩國不同色所需要的最少顏色數目Col(Sk)有上限:

其中的Sk是指虧格為k(有k個「洞」)的曲面(或者說二維可微流形),表示下取整函數。他還證明當虧格為1,也就是曲面為環面的時候,存在至少要用7種顏色才能染色的地圖。而環面對應的上限不等式是:
因此希伍德證明了:最多用7種顏色就能為任何環面上的地圖染色[17]:218[30]。
希伍德猜測,一般的曲面地圖染色中,上面的不等式也可以變成等式。他提出猜想:任意的可定向曲面上,最多只用種顏色就能為任意的地圖染色,其中k是曲面的虧格。這個猜想被稱為希伍德地圖染色問題或者希伍德猜想[17]:217。當k = 0的時候,這個猜想就變成四色猜想[30]。
進一步的推導可以將這個猜想分為12種情況。但僅僅在證明了其中一種和幾個較小的k的情況後,由於文獻上的誤導,不少數學家錯誤地以為問題已經得到解決。1950年後,有關的研究才重新開始。1968年,傑拉德·林格爾和約翰·威廉·西奧多·楊格斯最終證明了這個猜想在k ≥1時的情況[30]。而隨着1976年,k = 0情況(也就是四色定理)的最終證明,希伍德猜想最終獲得完整的解決。此後希伍德猜想也開始被稱為希伍德地圖定理或林格爾-楊格斯定理[17]:219。
參見
[編輯]- 圖染色
- 更加一般的染色問題,討論任意的圖的點或邊染色時的性質。
- 哈德維格-尼爾森問題
- 需要用多少種顏色給平面上的點染色,才能夠使任何兩個距離是1的點染的顏色都不同?
- 拉姆齊問題
- 最少要有幾個人,才能保證其中必然有k個人兩兩相識,或者l個人兩兩不相識?這等價於討論完全圖2-染色的性質。
- 曲面染色
參考文獻
[編輯]- ^ 潘永祥. 《自然科學概論》. 五南圖書出版股份有限公司. 1996: 532. ISBN 9789571111858 (中文).
- ^ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 2.17 2.18 2.19 2.20 2.21 2.22 2.23 2.24 2.25 2.26 2.27 2.28 2.29 2.30 Rudolf Fritsch, Gerda Fritsch. The Four-Color Theorem : History, Topological Foundations, and Idea of proof. Julie Peschke 譯. New York Berlin Heidelberg: Springer-Verlag. ISBN 0-387-98497-6 (英語).
- ^ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 Alexander Soifer. The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of Its Creators. Springer. 2009 [6 March 2013]. ISBN 978-0-387-74642-5 (英語).
- ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 Norman L. Biggs, E. Keith Lloyd, Robin J. Wilson. Graph Theory 1736-1936. Oxford University Press. 1999年. ISBN 978-0-198-53916-2 (英語).
- ^ C. EISELE. The new elements of mathematics by Charles S. Peirce Volume 3/1. Mouton. Den Haag. 1976: 476–7.
- ^ 6.0 6.1 6.2 6.3 6.4 Alfred Bray Kempe. On the geographical problem of the four colors. American Journal of Mathematics. 1879年9月3日, 2 (3): 193–200 [2013-03-02]. (原始內容存檔於2015年11月7日) (英語).
- ^ Fabian Franklin. William Edward Story (1850-1930). Proceedings of the American Academy of Arts and Sciences. 1936年3月, 70 (10): 578–580 [2013-03-01]. (原始內容存檔於2016-08-19) (英語).
- ^ 8.0 8.1 8.2 Professors Ralph Bravaco and Shai Simonson. The Four-Color Theorem. Stonehill College. [2013-03-02]. (原始內容存檔於2013-05-01) (英語).
- ^ S.D. ColliIngwood. The life and the letters of Lewis Carroll (Rev. C. L. Dodgson). London: Nelson. 1808 (英語).
- ^ E. Lucas. Récréations mathématiques. Paris: Vol 4. Gauthier-Villars. 1894 (法語).
- ^ Constance Reid. Hilbert. Springer. ed.2. 1996. ISBN 978-0-387-94674-0 (英語).
- ^ Mac Lane, Saunders. Oswald Veblen June 24, 1880—August 10, 1960. Biographical Memoirs of the Natl Acad Sci U S A (PDF). Washington, D.C. 1964 [2013-03-02]. (原始內容存檔 (PDF)於2015-04-02) (英語).
- ^ Robin Thomas. An Update on the Four-Color Theorem (PDF). Notices of American Mathematics Society. 1998, 45: 848–859 [2013-03-03]. (原始內容存檔 (PDF)於2010-03-31) (英語).
- ^ 14.0 14.1 Philip Franklin. The four color problem. American Journal of Mathematics. 1922, 44: 225–236 (英語).
- ^ Jeremy Preston Magee. Reducible Configurations and So On: The Final Years of the Four Color Theorem. ProQuest. 2008. ISBN 9780549559948 (英語).
- ^ J. J. O'Connor, E. F. Robertson. The four colour theorem. 猶他州大學. 1996年9月 [2013-03-03]. (原始內容存檔於2013-01-16) (英語).
- ^ 17.0 17.1 17.2 17.3 17.4 Gary Chartrand, Ping Zhang. Chromatic Graph Theory. CRC Press. 2008年. ISBN 9781584888017 (英語).
- ^ Postmarks Used by Department of Mathematics University of Illinois at Urbana-Champaign (PDF). [2013-03-04]. (原始內容 (PDF)存檔於2013-10-30).
- ^ K. Appel, W. Haken. Research Announcement : Every planar map is four colorable. Bull. Amer. Math. Soc. 1976年9月, 82 (5): 711–712 [2013-03-04]. (原始內容存檔於2013-07-27).
- ^ K. Appel, W. Haken. Every planar map is four colorable. Part I: Discharging. Illinois Journal of Mathematics. 1977, 21 (3): 429–490 [2018-02-17]. (原始內容存檔於2016-03-04).
- ^ K. Appel, W. Haken, J. Koch. Every planar map is four colorable. Part II: Reducibility. Illinois Journal of Mathematics. 1977, 21 (3): 491–567 [2013-03-04]. (原始內容存檔於2013-04-24).
- ^ Tımea Herczeg, Bernhelm Booss-Bavnbek. The Effect of Computers on Pure Mathematics (PDF). Roskilde University. 2009 [2013-03-04].[永久失效連結](英文)
- ^ Thomas Tymoczko. The Four-Color Problem and Its Philosophical Significance (PDF). The Journal of Philosophy. 1979年2月, 76 (2): 57–83 [2013-03-04]. (原始內容存檔 (PDF)於2014-02-20).(英文)
- ^ Paul C. Kainen. Is the four color theorem true?. Geombinatorics. 1993, 3 (2): 41–56.
- ^ Robin Thomas. An Update On The Four-Color Theorem (PDF). NOTICES AMER. MATH. SOC. 1998, 45: 848–859 [2013-03-08]. (原始內容存檔 (PDF)於2012-10-20).
- ^ 26.0 26.1 26.2 Robin Wilson. Four Colors Suffice. London: Penguin Books. 2002. ISBN 0-691-11533-8 (英語).
- ^ Richard Zach. Four Color Theorem Verified in Coq. [2013-03-08]. (原始內容存檔於2012-01-29).
- ^ Judith A. Tyner. Principles of Map Design. Guilford Press. 2010. ISBN 9781606235447 (英語).
- ^ Timothy Gowers, June Barrow-Green, Imre Leader. The Princeton Companion to Mathematics. London: Princeton University Press. 2010. ISBN 9781400830398 (英語).
- ^ 30.0 30.1 30.2 Gerhard Ringel, J.W.T.Youngs. Solution of the Heawood Map-coloring Problem (PDF). Proceedings of the National Academy of Science of the U.S.A. 1968, 60 (2): 438–445 [2013-03-11]. (原始內容存檔 (PDF)於2021-11-08) (英語).
外部連結
[編輯]- Hazewinkel, Michiel (編), Four-colour problem, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
- 埃里克·韋斯坦因. Blanuša snarks. MathWorld.
- 埃里克·韋斯坦因. Map coloring. MathWorld.



![{\displaystyle C=\{c(t);\quad t\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1a7bf3408dcde70924830bc5cd9b1cdb6cbdf1c)





![{\displaystyle \forall 1\leqslant i\leqslant m,\,C_{i}=\{c_{i}(t);\quad t\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8dbde22e9771e0597e0c85da8857498e3e575b)



















