 單位矩形的四個角的z值分別是0、1、1、0.5,如果將坐標解釋為顏色,整個單位矩形上的雙線性插值結果如圖。
單位矩形的四個角的z值分別是0、1、1、0.5,如果將坐標解釋為顏色,整個單位矩形上的雙線性插值結果如圖。
雙線性插值,又稱為雙線性內插。在數學上,雙線性插值是對線性插值在二維直角網格上的擴展,用於對雙變量函數(例如 x 和 y)進行插值。其核心思想是在兩個方向分別進行一次線性插值。
 紅色的數據點與待插值得到的綠色點
紅色的數據點與待插值得到的綠色點
假如我們想得到未知函數 f 在點  的值,假設我們已知函數 f 在
的值,假設我們已知函數 f 在  ,
,  ,
,  , 及
, 及  四個點的值。
四個點的值。
首先在 x 方向進行線性插值,得到

然後在 y 方向進行線性插值,得到

注意此處如果先在 y 方向插值、再在 x 方向插值,其結果與按照上述順序雙線性插值的結果是一樣的。
如果選擇一個坐標系統使得 f 的四個已知點坐標分別為 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那麼插值公式就可以化簡為

或者用矩陣運算表示為

顧名思義,雙線性插值的結果不是線性的,它是兩個線性函數的積。在單位正方形上,雙線性插值可以記作

常數的數目(四)對應於給定的 f 的數據點數目




雙線性插值的結果與插值的順序無關。首先進行 y 方向的插值,然後進行 x 方向的插值,所得到的結果是一樣的。
雙線性插值的一個顯然的三維空間延伸是三線性插值。
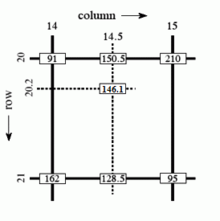 對灰度值進行雙線性插值
對灰度值進行雙線性插值
在計算機視覺及圖像處理領域,雙線性插值是一種基本的重採樣技術。
材質貼圖中,雙線性插值也叫雙線性過濾或者雙線性材質貼圖。圖像的雙線性插值放大算法中,目標圖像中新創造的象素值,是由源圖像位置在它附近的2*2區域4個鄰近象素的值通過加權平均計算得出的。雙線性內插值算法放大後的圖像質量較高,不會出現像素值不連續的的情況。然而此算法具有低通濾波器的性質,使高頻分量受損,所以可能會使圖像輪廓在一定程度上變得模糊。

















