Gamma|
機率密度函數 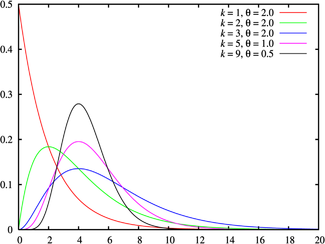 |
|
累積分佈函數 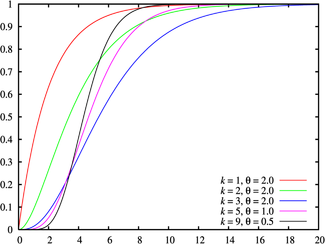 |
| 參數 |
 形狀參數 (實數) 形狀參數 (實數)
 尺度參數 (實數) 尺度參數 (實數) |
|---|
| 值域 |
 |
|---|
| 機率密度函數 |
 |
|---|
| 累積分佈函數 |
 |
|---|
| 期望值 |
 |
|---|
| 中位數 |
no simple closed form |
|---|
| 眾數 |
 for for  |
|---|
| 變異數 |
 |
|---|
| 偏度 |
 |
|---|
| 峰度 |
 |
|---|
| 熵 |

 |
|---|
| 動差母函數 |
 for for  |
|---|
| 特徵函數 |
 |
|---|
伽瑪分佈(英語:Gamma distribution)是統計學的一種連續機率分佈。伽瑪分佈中的參數α,稱為形狀參數,β稱為尺度參數。
假設X1, X2, ... Xn 為連續發生事件的等候時間,且這n次等候時間為獨立的,那麼這n次等候時間之和Y (Y=X1+X2+...+Xn)服從伽瑪分佈,即 Y~Gamma(α , β),亦可記作Y~Gamma(α , λ),其中α = n,而 β 與λ互為倒數關係,λ 表單位時間內事件的發生率。
指數分佈為α = 1的伽瑪分佈。
有兩種表記方法:
 或
或
兩者所表達意義相同,只要將以下式子做 的替換即可,即,其機率密度函數為:
的替換即可,即,其機率密度函數為:
 ,x > 0
,x > 0
其中Gamma函數之特徵為:


![{\displaystyle K_{x}\left(t\right)=\ln M_{x}\left(t\right)=\alpha \left[\ln \lambda -\ln \left(\lambda -t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3c9932ee15d43b2588004f15ca6294b05b4462)


當兩隨機變量服從Gamma分佈,且相互獨立,且參數( 或
或 )相同時,Gamma分佈具有可加性。
)相同時,Gamma分佈具有可加性。



 形狀參數 (實數)
形狀參數 (實數) 尺度參數 (實數)
尺度參數 (實數)



 for
for 





 for
for 










![{\displaystyle K_{x}\left(t\right)=\ln M_{x}\left(t\right)=\alpha \left[\ln \lambda -\ln \left(\lambda -t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3c9932ee15d43b2588004f15ca6294b05b4462)




