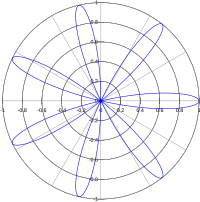
 七個瓣的玫瑰線
七個瓣的玫瑰線
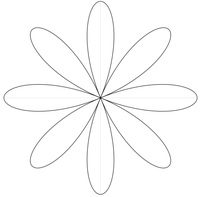 八個瓣的玫瑰線(k=4)
八個瓣的玫瑰線(k=4)
 各種各樣的玫瑰線
各種各樣的玫瑰線
玫瑰線是極坐標系中的正弦曲線,可以用以下的方程來表示:

如果k是偶數,玫瑰線就有2k個瓣,如果k是奇數,則有k個瓣。
如果k是有理數,玫瑰線就是封閉的,其長度有限。如果k是無理數,則曲線不是封閉的,長度為無窮大。在這種情況下,玫瑰線的圖形便形成了一個稠密集。
由於對於所有的 ,都有:
,都有:

因此由以下方程所確定的玫瑰線
 和
和
除了角度的不同以外,是全等的。
由以下方程所確定的玫瑰線

其中k是正整數,具有面積:

如果k是偶數;

如果k是奇數。
相同的公式也適用於以下形式的玫瑰線:
