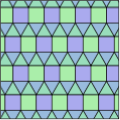
柱形五邊形鑲嵌
外觀
 歐幾里得平面 | ||
| 類別 | 半正鑲嵌對偶 平面鑲嵌 | |
|---|---|---|
| 對偶多面體 | 異扭稜正方形鑲嵌 | |
| 數學表示法 | ||
| 施萊夫利符號 | d({3,6}:e) | |
| 康威表示法 | d(dH:e) | |
| 性質 | ||
| 二面角 | 平角 | |
| 組成與佈局 | ||
| 面的種類 | 對稱不規則五邊形 | |
| 面的佈局 | V3.3.3.4.4 | |
| 對稱性 | ||
| 對稱群 | cmm, [∞,2+,∞], (2*22) | |
| 旋轉對稱群 | p2, [∞,2,∞]+, (2222) | |
| 特性 | ||
| 面可遞 | ||
| 圖像 | ||
| ||
在幾何學中,柱形五邊形鑲嵌是一種平面鑲嵌,其為半正鑲嵌異扭稜正方形鑲嵌的對偶鑲嵌[1],密鋪於歐氏平面,是15種已知的等面五邊形鑲嵌之一。
康威稱柱形五邊形鑲嵌為iso(4-)pentille[2],因為它五邊形以四階拼合但又與實際上的四階不太相同,因此以iso(異)稱呼。
此鑲嵌由一種五邊形獨立密鋪,該五邊形具有三個120度角和二個90度角,可以看作是由正方形和一個120度的鈍角等腰三角形,也可以視為退化的二角錐柱,因此稱為柱形五邊形鑲嵌。
參見
[編輯]參考文獻
[編輯]- Grünbaum, Branko ; and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p.58-65)
- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. p37
- H.S.M. Coxeter, Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (頁面存檔備份,存於互聯網檔案館)
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] p 276
- ^ Weisstein, Eric W. (編). Dual tessellation. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 存档副本. [2012-01-20]. (原始內容存檔於2010-09-19). (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table)