| 完全二分圖 |
|---|
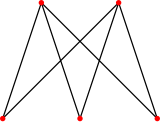 一個完全二分圖m=3 n =2 |
| 頂點 | n+m |
|---|
| 邊 | mn |
|---|
| 自同構群 | 2m!n!如果m=n,否則m!n! |
|---|
|
完全二分圖是一種特殊的二分圖,可以把圖中的頂點分成兩個集合,使得第一個集合中的所有頂點都與第二個集合中的所有頂點相連。
完全二分圖 是一個二分圖,使得對於任何兩個頂點
是一個二分圖,使得對於任何兩個頂點 和
和 ,
, 都是
都是 中的一條邊。
中的一條邊。 且
且 的完全二分圖記為
的完全二分圖記為 。
。
- 平面圖不能含有子圖
 ;外平面圖不能含有子圖
;外平面圖不能含有子圖 (這些是必要條件而不是充分條件)。
(這些是必要條件而不是充分條件)。
- 完全二分圖
 的頂點覆蓋數為
的頂點覆蓋數為 ,邊覆蓋數為
,邊覆蓋數為 。
。
- 完全二分圖
 具有大小為
具有大小為 的最大獨立集。
的最大獨立集。
- 完全二分圖
 具有大小為
具有大小為 的最大匹配。
的最大匹配。
- 完全二分圖
 具有正則的n-邊染色。
具有正則的n-邊染色。
- 完全二分圖
 有mn-1 nm-1個不同的生成樹。
有mn-1 nm-1個不同的生成樹。

















