垂直軸定理

在物理學裏，垂直軸定理（也叫「正交軸定理」）可以用來計算一片薄片的轉動慣量。思考一個直角座標系，其中兩個座標軸都包含與平行於此薄片；如果已知此薄片對於這兩個座標軸的轉動慣量，則垂直軸定則可以用來計算薄片對於第三個座標軸的轉動慣量。

假設OXYZ座標系統的 X-軸與 Y-軸都包含與平行於此薄片，而 Z-軸垂直於薄片的面。$I_{X}\,\!$ 與 $I_{Y}\,\!$ 分別代表薄片對於 X-軸與 Y-軸的轉動慣量．那麼，薄片對於 Z-軸的轉動慣量為

$I_{Z}=I_{X}+I_{Y}\,\!$ 。

垂直軸定理、平行軸定理、與伸展定則可以用來計算許多不同形狀的物體的轉動慣量。

導引

厚度很薄的薄片

任何實際存在的剛體都有厚度；不可能有零厚度的剛體。參考右圖，假設這剛體是一塊很薄的薄片，厚度 $t\,\!$ 是均勻的，密度也是均勻的。設定薄片的面與 XY-面共平面。那麼，剛體對於 X-軸、Y-軸、與 Z-軸的轉動慣量分別為

$I_{X}=\int (y^{2}+z^{2})\;dm\,\!$ 、

$I_{Y}=\int (x^{2}+z^{2})\;dm\,\!$ 、

$I_{Z}=\int (x^{2}+y^{2})\;dm\,\!$ 。

由於厚度超小於薄片的面尺寸，我們可以忽略 $z^{2}\,\!$ 對於積分的貢獻．因此，

$I_{X}\approx \int y^{2}\;dm\,\!$ 、

$I_{Y}\approx \int x^{2}\;dm\,\!$ 。

所以，

$I_{Z}=I_{X}+I_{Y}\,\!$ 。

實例

薄圓盤

a) 如右圖，一個半徑為 $r\,\!$，質量為 $m\,\!$ 的薄圓盤，對於 Z-軸的轉動慣量為

$I_{Z}={\frac {1}{2}}mr^{2}\,\!$ 。

所以，對於X-軸與 Y-軸的轉動慣量是

$I_{X}=I_{Y}={\frac {I_{Z}}{2}}={\frac {1}{4}}mr^{2}\,\!$ 。

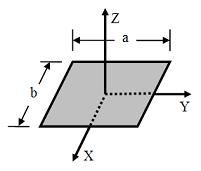長方形薄片

b) 如右圖，一個尺寸為 $a\times b\,\!$，質量為 $m\,\!$ 的長方形薄片,對於 X-軸、Y-軸、與 Z-軸的轉動慣量分別為

$I_{X}={\frac {1}{12}}ma^{2}\,\!$ 、

$I_{Y}={\frac {1}{12}}mb^{2}\,\!$ 、

$I_{Z}={\frac {1}{12}}m(a^{2}+b^{2})\,\!$ 。

很明顯地，

$I_{Z}=I_{X}+I_{Y}\,\!$ 。

參考文獻

• 程稼夫. 中学奥林匹克竞赛物理教程.力学篇 第2版. 中國科技大學出版社. 2013: 281. ISBN 978-7-312-03193-9 （中文（中國大陸））. 

參閱

• 轉動慣量列表
• 平行軸定理