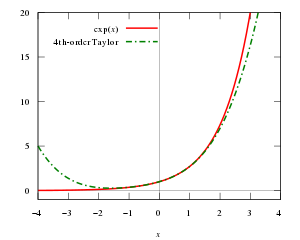
 指數函數
指數函數 (紅色實線)與在原點展開的泰勒多項式前四項(綠色虛線)。在這個函數中,泰勒多項式展開的項數越多,曲線擬合得越好。
(紅色實線)與在原點展開的泰勒多項式前四項(綠色虛線)。在這個函數中,泰勒多項式展開的項數越多,曲線擬合得越好。
在數學中,泰勒公式(英語:Taylor's Formula)是一個用函數在某點的信息描述其附近取值的公式。這個公式來自於微積分的泰勒定理(Taylor's theorem),泰勒定理描述了一個可微函數,如果函數足夠光滑的話,在已知函數在某一點的各階導數值的情況之下,泰勒公式可以用這些導數值做係數構建一個多項式來近似函數在這一點的鄰域中的值,這個多項式稱為泰勒多項式(Taylor polynomial)。泰勒公式還給出了餘項即這個多項式和實際的函數值之間的偏差。泰勒公式得名於英國數學家布魯克·泰勒。他在1712年的一封信里首次敘述了這個公式,儘管1671年詹姆斯·格雷高里已經發現了它的特例[1]。拉格朗日在1797年之前,最先提出了帶有餘項的現在形式的泰勒定理。
泰勒公式的初衷是用多項式來近似表示函數在某點周圍的情況。比如說,指數函數 在
在 的附近可以用以下多項式來近似地表示:
的附近可以用以下多項式來近似地表示:

稱為指數函數在0處的 階泰勒展開公式。這個公式只對
階泰勒展開公式。這個公式只對 附近的
附近的 有用,
有用, 離
離 越遠,這個公式就越不準確。實際函數值和多項式的偏差稱為泰勒公式的餘項。
越遠,這個公式就越不準確。實際函數值和多項式的偏差稱為泰勒公式的餘項。

對於一般的函數,泰勒公式的係數的選擇依賴於函數在一點的各階導數值。這個想法的原由可以由微分的定義開始。微分是函數在一點附近的最佳線性近似:
 ,其中
,其中 是比h 高階的無窮小。
是比h 高階的無窮小。
也就是說 ,或
,或 。
。
注意到 和
和 在a 處的零階導數和一階導數都相同。對足夠光滑的函數,如果一個多項式在a 處的前n 次導數值都與函數在a 處的前n 次導數值重合,那麼這個多項式應該能很好地近似描述函數在a 附近的情況。以下定理說明這是正確的:
在a 處的零階導數和一階導數都相同。對足夠光滑的函數,如果一個多項式在a 處的前n 次導數值都與函數在a 處的前n 次導數值重合,那麼這個多項式應該能很好地近似描述函數在a 附近的情況。以下定理說明這是正確的:
定理:
設 n 是一個正整數。如果定義在一個包含 a 的區間上的函數 f 在 a 點處 n+1 次可導,那麼對於這個區間上的任意 x,都有:
 [2]
[2]
其中的多項式稱為函數在a 處的泰勒展開式,剩餘的 是泰勒公式的餘項,是
是泰勒公式的餘項,是 的高階無窮小。
的高階無窮小。
 的表達形式有若干種,分別以不同的數學家命名。
的表達形式有若干種,分別以不同的數學家命名。
帶有皮亞諾型餘項的泰勒公式說明了多項式和函數的接近程度:
![{\displaystyle f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f^{(2)}(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c623c29664a9d7ca96525f7e7293d4f9a5d3e01)
也就是說,當x 無限趨近a 時,餘項 將會是
將會是 的高階無窮小,或者說多項式和函數的誤差將遠小於
的高階無窮小,或者說多項式和函數的誤差將遠小於 [3]。這個結論可以由下面更強的結論推出。
[3]。這個結論可以由下面更強的結論推出。
帶有拉格朗日型餘項的泰勒公式可以視為拉格朗日微分中值定理的推廣:

即 ,其中
,其中 [4]。
[4]。
帶有積分型餘項的泰勒公式可以看做微積分基本定理的推廣[5]:

拉格朗日型餘項或積分型餘項可以幫助估計泰勒展開式和函數在一定區間之內的誤差。設函數在區間[a − r, a + r] 上n 次連續可微並且在區間(a − r, a + r) 上n + 1 次可導。如果存在正實數Mn 使得區間(a − r, a + r) 里的任意x 都有  ,那麼:
,那麼:

其中 。這個上界估計對區間(a − r, a + r) 里的任意x 都成立,是一個一致估計。
。這個上界估計對區間(a − r, a + r) 里的任意x 都成立,是一個一致估計。
如果當n 趨向於無窮大時,還有 ,那麼可以推出
,那麼可以推出  ,f 是區間(a − r, a + r) 上解析函數。f 在區間(a − r, a + r) 上任一點的值都等於在這一點的泰勒展開式的極限。
,f 是區間(a − r, a + r) 上解析函數。f 在區間(a − r, a + r) 上任一點的值都等於在這一點的泰勒展開式的極限。
對於多元函數,也有類似的泰勒公式。設B(a, r ) 是歐幾里得空間RN 中的開球,ƒ 是定義在B(a, r ) 的閉包(即閉球)上的實值函數,並在每一點都存在所有的n+1 次偏導數。這時的泰勒公式為:
- 對所有
 ,
,

- 其中的
 是多重指標,即
是多重指標,即 ,
,  。
。
- 若
 ,則記 :
,則記 : ,
, .
.
其中的餘項也滿足不等式:
- 對所有滿足 |α| = n + 1 的 α,

特別地,多元形式的泰勒公式可表示為:

- 其中
 .
.
在應用上述公式時,特別重要的是展開式的前三項,即:
 .
.- 運用雅可比矩陣與海森矩陣,則上式可表示為:

- 其中
 為雅可比矩陣,
為雅可比矩陣, 為海森矩陣.
為海森矩陣.
- ^ J J O'Connor and E F Robertson. Brook Taylor's Biography. [2009-12-25]. (原始內容存檔於2010-11-20).
- ^ Rudin, 第123至124頁.
- ^ 《微積分(Ⅱ)》第88-90頁.
- ^ Klein (1998) 20.3; Apostol (1967) 7.7
- ^ Protter, Morrey, 第135-136頁



















![{\displaystyle f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f^{(2)}(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+o[(x-a)^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c623c29664a9d7ca96525f7e7293d4f9a5d3e01)























