實外代數中,
n 階元素的幾何詮釋:
n = 0(具有正負號的點),1(具有指向的線段,即
向量),2(具有定向的平面元),3(具有定向的體積)。
n個向量的外積可以圖像化為
n維幾何物體(例如
n維
平行六面體,
n維
橢球);其大小為
超體積(hypervolume),其
定向的定義由
(n − 1)維邊界以及物體內部在哪一側來決定。
[1][2]外代數(英語:Exterior algebra)也稱為格拉斯曼代數(Grassmann algebra),以紀念數學家赫爾曼·格拉斯曼。
數學上,向量空間 的外代數是一個特定有單位的結合代數,其包含了
的外代數是一個特定有單位的結合代數,其包含了 為其中一個子空間。它記為
為其中一個子空間。它記為 或
或 . 而它的乘法,稱為楔積或外積,記為
. 而它的乘法,稱為楔積或外積,記為 . 楔積是結合的和雙線性的;其基本性質是它在
. 楔積是結合的和雙線性的;其基本性質是它在 上是交錯的,也就是:
上是交錯的,也就是:
 ,對於所有向量
,對於所有向量
這表示
 ,對於所有向量
,對於所有向量 ,以及
,以及 ,當
,當 線性相關時。
線性相關時。
值得注意的是,以上三性質只對 中向量成立,不是對代數
中向量成立,不是對代數 中所有向量成立。
中所有向量成立。
外代數事實上是「最一般的」滿足這些屬性的代數。這意味着所有在外代數中成立的方程只從上述屬性就可以得出。 的這個一般性形式上可以用一個特定的泛性質表示,請參看下文。
的這個一般性形式上可以用一個特定的泛性質表示,請參看下文。
形式為 的元素,其中
的元素,其中 在
在 中,稱為
中,稱為 -向量。所有
-向量。所有 -向量生成的
-向量生成的 的子空間稱為
的子空間稱為 的
的 -階外冪,記為
-階外冪,記為 。外代數可以寫作每個
。外代數可以寫作每個 階冪的直和:
階冪的直和:

該外積有一個重要性質,就是 -向量和
-向量和 -向量的積是一個
-向量的積是一個 -向量。這樣外代數成為一個分次代數,其中分級由
-向量。這樣外代數成為一個分次代數,其中分級由 給出。這些
給出。這些 -向量有幾何上的解釋:2-向量
-向量有幾何上的解釋:2-向量 代表以
代表以 和
和 為邊的帶方向的平行四邊形,而3-向量
為邊的帶方向的平行四邊形,而3-向量 代表帶方向的平行六面體,其邊為
代表帶方向的平行六面體,其邊為 ,
,  , 和
, 和 。
。
外冪的主要應用在於微分幾何,其中他們用來定義微分形式。因而,微分形式有一個自然的楔積。所有這些概念由格拉斯曼提出。
外代數有很多種等價的定義,下面的定義是最簡潔的一個。
定義: 設  是域
是域  上的一個向量空間,讓
上的一個向量空間,讓 則定義
則定義

令  為
為  的張量代數的理想(即雙邊理想),該理想是由所有形如
的張量代數的理想(即雙邊理想),該理想是由所有形如 的張量生成的(其中
的張量生成的(其中 任意),則將
任意),則將 上的外代數
上的外代數 定義為商代數
定義為商代數 ,即
,即

並且把 的等價類[3]
的等價類[3] ![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in T(V)/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cc22666c1170f17014dfeffe7f75615447a4) 記為
記為 ,其中
,其中  。設
。設 稱
稱

為 的
的 -階外冪(
-階外冪( th exterior power of
th exterior power of  ),稱
),稱 中的元素為
中的元素為 -向量(
-向量( -multivector)。
-multivector)。
註:
 ,當且僅當
,當且僅當 時才有
時才有 ,因此,可以把
,因此,可以把 等同於
等同於 ,並且把
,並且把![{\displaystyle [\lambda ]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87059ecf792985dc56378febbb4b00f6206e3f7b) 記為
記為 ;基於類似的原因,可以把
;基於類似的原因,可以把 等同於
等同於 ,而且把
,而且把![{\displaystyle [v]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9046713e2b3df3c380f0953dddd1217fc78741) 記為
記為 。這一點是前面所講的能夠把
。這一點是前面所講的能夠把![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in \Lambda ^{k}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d259aecf2ba50066504b749521bef64542076b) 記為
記為  的特例和前提。
的特例和前提。- 當
 時,
時, -向量並不僅限於形如
-向量並不僅限於形如 的元素,例如,
的元素,例如, 也是2-向量,其中
也是2-向量,其中 .
.
- 理想
 中的元素並不僅限於形如
中的元素並不僅限於形如 的張量,例如,
的張量,例如,
 , 必定有
, 必定有  和
和 .
. , 由於
, 由於 和
和 以及
以及 ,顯然有
,顯然有 ,這就有一個推論:所有的二階對稱張量都在理想
,這就有一個推論:所有的二階對稱張量都在理想 中。
中。- 由於上面的兩個結論,
 ,我們有
,我們有 ,這是因為等式右邊的每一項都在
,這是因為等式右邊的每一項都在 中。對張量
中。對張量 的階數作數學歸納法,則可以證明:
的階數作數學歸納法,則可以證明: ,
,  ,總有
,總有 。
。
- 設
 ,則
,則 ,
, 作為等價類含有唯一的一個完全反對稱的代表元
作為等價類含有唯一的一個完全反對稱的代表元 ,可以把這個
,可以把這個 -階的完全反對稱張量等同於
-階的完全反對稱張量等同於 , 詳見後面的「反對稱算子和外冪」一節。在有些文獻中,
, 詳見後面的「反對稱算子和外冪」一節。在有些文獻中, -向量就是以這種方式定義的。
-向量就是以這種方式定義的。
運算律 將上面的注中的內容用 寫出,則分別給出
寫出,則分別給出
(1)  ,
, 
證明如下: 作為等價類,我們從 中任意挑選一個代表元
中任意挑選一個代表元 ,則
,則 而且
而且![{\displaystyle \alpha =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be72fb8369a0b6808989320d3eba4c86f429909) 。根據商代數的定義,
。根據商代數的定義,
![{\displaystyle \lambda \wedge \alpha =[\lambda ]\wedge [t]=[\lambda \otimes t]=[\lambda t]=\lambda [t]=\lambda \alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ede685179f9a4a99660bdcab23fc2cdb426b2599)
類似地,可以證明
(2) 根據注3.1中的內容,顯然有 .
.
(3) 根據注3.2中的內容,對任意 成立着
成立着

註:即使 的特徵為2,這個公式也是對的,只不過此時有
的特徵為2,這個公式也是對的,只不過此時有 而已。
而已。
(4) 根據商代數的定義以及張量代數的性質,運算 滿足結合律和分配律:
滿足結合律和分配律:



其中 都是任意的。
都是任意的。
以前兩條性質為例,其證明如下:設張量 分別是
分別是 中的代表元,即
中的代表元,即![{\displaystyle \alpha =[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c56dee62ec8838b6cd786c13216890455a5d1d2) ,
, ![{\displaystyle \beta =[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c935f2f60cd1e8d9d077d735f6d130ee5a74db1) ,
, ![{\displaystyle \theta =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0c8f339935b23b31c47564f326e8b93f9f9b8b) , 則
, 則
![{\displaystyle (\alpha \wedge \beta )\wedge \theta =([a]\wedge [b])\wedge [t]=[a\otimes b]\wedge [t]=[(a\otimes b)\otimes t]=[a\otimes (b\otimes t)]=[a]\wedge [b\otimes t]=[a]\wedge ([b]\wedge [t])=\alpha \wedge (\beta \wedge \theta ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a92cda22d4dd50698f5df8052dddf5c3c1d9745)
![{\displaystyle (\alpha +\beta )\wedge \theta =([a]+[b])\wedge [t]=[a+b]\wedge [t]=[(a+b)\otimes t]=[a\otimes t+b\otimes t]=[a\otimes t]+[b\otimes t]=[a]\wedge [t]+[b]\wedge [t]=\alpha \wedge \theta +\beta \wedge \theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3731bec5812efe5762122dc15bdbca47fc40a1b4)
(5) 根據上面的(3)和(4),用數學歸納法可以證明:

證明從略。
若 的維數是
的維數是 而
而 是
是 的基,則集合
的基,則集合

是 階外冪
階外冪 的一個基。理由如下:給定任何如下形式的楔積
的一個基。理由如下:給定任何如下形式的楔積

則每個向量 可以記為基向量
可以記為基向量 的一個線性組合;利用楔積的雙線性性質,這可以擴張為那些基向量的楔積的線性組合。任何出現同樣基向量兩次的楔積為0;任何基向量出現的次序不正確的可以重新排序,在交換任何兩個基向量的時候變換符號。一般來講,最後基
的一個線性組合;利用楔積的雙線性性質,這可以擴張為那些基向量的楔積的線性組合。任何出現同樣基向量兩次的楔積為0;任何基向量出現的次序不正確的可以重新排序,在交換任何兩個基向量的時候變換符號。一般來講,最後基 -向量前的係數可以用通過積
-向量前的係數可以用通過積 來描述
來描述 的矩陣的子式來計算。
的矩陣的子式來計算。
數一下基元素,我們可以看到 的維數是n 取 k。特別的有,
的維數是n 取 k。特別的有,
 對於
對於 .
.
外代數是一個分級代數,是如下直和

其維數等於二項式係數之和,也就是 .
.
考慮空間 ,其基為
,其基為 。一對向量
。一對向量


的楔積為

其中 是三維空間
是三維空間 的基底。
的基底。
再加一個向量
 ,
,
這三個向量的楔積是

其中 是一維空間
是一維空間 的基底。
的基底。
空間 是
是 , 而空間
, 而空間 是
是 。取所有四個子空間的直和得到一個向量空間
。取所有四個子空間的直和得到一個向量空間 ,這是八維向量空間
,這是八維向量空間
 .
.
那麼,給定一對8維向量 和
和 , 其中
, 其中 如上給出,而
如上給出,而
 ,
,
 和
和 的楔積如下(用列向量表達),
的楔積如下(用列向量表達),
 .
.
容易驗證8維楔積以向量 為乘法幺元。也可以驗證該
為乘法幺元。也可以驗證該 代數的楔積是結合的(也是雙線性的):
代數的楔積是結合的(也是雙線性的):

所以該代數是有單位且結合的。
對三維歐幾里得空間 可以建立一個線性同構
可以建立一個線性同構 如下:任取
如下:任取 的右手的標準正交基
的右手的標準正交基 ,
, ,
, ,規定
,規定 把
把 ,
, ,
, 分別映射為
分別映射為 ,
, ,
, ,則
,則 的定義與右手的標準正交基如何選取無關。
的定義與右手的標準正交基如何選取無關。
不難看出,對任意向量 和
和 ,這個線性同構把
,這個線性同構把 映射為
映射為 。這就是叉乘(向量積)的實質。例如,
。這就是叉乘(向量積)的實質。例如, 中平行四邊形
中平行四邊形 的面積向量可以表示為
的面積向量可以表示為 . 經過推廣之後,高維黎曼流形
. 經過推廣之後,高維黎曼流形 中的緊的二維曲面
中的緊的二維曲面 的面積則可以用
的面積則可以用

來計算(其中 是度規張量場
是度規張量場 在
在 上的誘導度規
上的誘導度規
 的坐標分量),由此可以看到外積和叉乘的深刻關係。
的坐標分量),由此可以看到外積和叉乘的深刻關係。
在物理學中,向量(極向量)與贗向量(軸向量)兩個概念經常需要加以區分。從根本上說,向量是 中的元素,所以在空間反演變換下不會改變方向;而贗向量其實是
中的元素,所以在空間反演變換下不會改變方向;而贗向量其實是 中的元素,故在空間反演變換下會改變方向。
中的元素,故在空間反演變換下會改變方向。
類似地,藉助於右手的標準正交基,可以把 中的元素
中的元素 映射為「標量"
映射為「標量" 。但是,在空間反演變換下它就會原形畢露,所以稱它為贗標量。真正的標量在空間反演下是不變的,而贗標量在空間反演下會改變符號。
。但是,在空間反演變換下它就會原形畢露,所以稱它為贗標量。真正的標量在空間反演下是不變的,而贗標量在空間反演下會改變符號。
把 2-向量 映射為向量
映射為向量 以及把 3-向量
以及把 3-向量 映射為一個實數
映射為一個實數 的映射實際上是一個叫做霍奇對偶的線性映射。
的映射實際上是一個叫做霍奇對偶的線性映射。
令 為一個域
為一個域 (在多數應用中,也就是實數域)上的向量空間。
(在多數應用中,也就是實數域)上的向量空間。 是「最一般」的包含
是「最一般」的包含 的並有一個交替乘法在
的並有一個交替乘法在 上由單位的結合
上由單位的結合 -代數這個事實可以用如下的泛性質形式化的表達:
-代數這個事實可以用如下的泛性質形式化的表達:
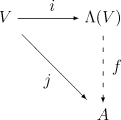 外代數的泛性質
外代數的泛性質
要構造最一般的包含 的代數,而且其乘法是在
的代數,而且其乘法是在 上交替的,很自然可以從包含
上交替的,很自然可以從包含 的最一般的代數開始,也就是張量代數
的最一般的代數開始,也就是張量代數 ,然後通過合適的商來強制交替的性質。這樣我們取
,然後通過合適的商來強制交替的性質。這樣我們取 中由所有形為
中由所有形為 的元素生成的雙邊理想
的元素生成的雙邊理想 ,其中
,其中 屬於
屬於 ,並定義
,並定義 為商
為商

(並且使用 為
為 中的乘法的代號)。然後可以直接證明
中的乘法的代號)。然後可以直接證明 包含
包含 並且滿足上述泛性質。
並且滿足上述泛性質。
如果不是先定義 然後把外冪
然後把外冪 等同為特定的子空間,我們也可以先定義空間
等同為特定的子空間,我們也可以先定義空間 然後把它們合併成為一個代數
然後把它們合併成為一個代數 。這個方法在微分集合中常常用到,並在下節中有描述。
。這個方法在微分集合中常常用到,並在下節中有描述。
給定兩個向量空間 和
和 ,一個從
,一個從 到
到 的反對稱算子是一個多線性映射
的反對稱算子是一個多線性映射

使得只要 是
是 中線性相關的向量,則
中線性相關的向量,則
 .
.
最著名的例子是行列式值,從 到
到 的反對稱線形算子。
的反對稱線形算子。
映射

它關聯 中的
中的 個向量到他們的楔積,也就是它們相應的
個向量到他們的楔積,也就是它們相應的 -向量,這也是反對稱的。事實上,這個映射是定義在
-向量,這也是反對稱的。事實上,這個映射是定義在 上的「最一般」的反對稱算子:給定任何其它反對稱算子
上的「最一般」的反對稱算子:給定任何其它反對稱算子 ,存在一個唯一的線性映射
,存在一個唯一的線性映射 。這個泛性質表述了空間
。這個泛性質表述了空間 並且可以作為它的定義。
並且可以作為它的定義。
所有從 到基域
到基域 的反對稱映射組成一個向量空間,因為兩個這樣的映射的和、或者這樣一個映射和一個標量的乘積也是反對稱的。若
的反對稱映射組成一個向量空間,因為兩個這樣的映射的和、或者這樣一個映射和一個標量的乘積也是反對稱的。若 是有限維的,維數
是有限維的,維數 ,則該空間可以認同為
,則該空間可以認同為 ,其中
,其中 表示
表示 的對偶空間。特別的有,從
的對偶空間。特別的有,從 到
到 的反對稱映射的空間是
的反對稱映射的空間是 取
取 維的。
維的。
在這個等同關係下,若基域是 或者
或者 ,楔積有一個具體的形式:它從兩個給定的反對稱映射得到一個新的反對稱映射。設
,楔積有一個具體的形式:它從兩個給定的反對稱映射得到一個新的反對稱映射。設 和
和 為兩個反對稱映射。和在多線性映射的張量積的情況一樣,楔積的變量數是每個映射的變量數之和。它定義如下:
為兩個反對稱映射。和在多線性映射的張量積的情況一樣,楔積的變量數是每個映射的變量數之和。它定義如下:

其中多線性映射的交替 定義為其變量的所有排列的帶符號平均:
定義為其變量的所有排列的帶符號平均:

注意: 有一些書中楔積定義為

在主要由物理學家使用的指標記法中有:

令 為一個微分流形。一個微分k-形式
為一個微分流形。一個微分k-形式 是
是 (
( 的餘切叢的
的餘切叢的 階外冪)的一個截面。等價的有:
階外冪)的一個截面。等價的有: 是
是 的光滑函數,對於
的光滑函數,對於 的每個點
的每個點 給定一個
給定一個 的元素。大致來講,微分形式是餘切向量的全局版本。微分形式是微分幾何的重要工具,其中,它們被用於定義德拉姆上同調和亞歷山大-斯潘尼爾上同調。
的元素。大致來講,微分形式是餘切向量的全局版本。微分形式是微分幾何的重要工具,其中,它們被用於定義德拉姆上同調和亞歷山大-斯潘尼爾上同調。
給定一個交換環 和一個
和一個 -模
-模 ,我們可以定義和上文一樣的外代數
,我們可以定義和上文一樣的外代數 ,它是張量代數
,它是張量代數 適當的商。它會滿足類似的泛性質。
適當的商。它會滿足類似的泛性質。
格拉斯曼代數在物理中有重要應用,它們被用於建模和費米子和超對稱性相關的各種概念。
參看:超空間,超代數,超群
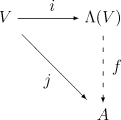

































![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in T(V)/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cc22666c1170f17014dfeffe7f75615447a4)







![{\displaystyle [\lambda ]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87059ecf792985dc56378febbb4b00f6206e3f7b)


![{\displaystyle [v]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9046713e2b3df3c380f0953dddd1217fc78741)
![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in \Lambda ^{k}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d259aecf2ba50066504b749521bef64542076b)

























![{\displaystyle \alpha =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be72fb8369a0b6808989320d3eba4c86f429909)
![{\displaystyle \lambda \wedge \alpha =[\lambda ]\wedge [t]=[\lambda \otimes t]=[\lambda t]=\lambda [t]=\lambda \alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ede685179f9a4a99660bdcab23fc2cdb426b2599)












![{\displaystyle \alpha =[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c56dee62ec8838b6cd786c13216890455a5d1d2)
![{\displaystyle \beta =[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c935f2f60cd1e8d9d077d735f6d130ee5a74db1)
![{\displaystyle \theta =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0c8f339935b23b31c47564f326e8b93f9f9b8b)
![{\displaystyle (\alpha \wedge \beta )\wedge \theta =([a]\wedge [b])\wedge [t]=[a\otimes b]\wedge [t]=[(a\otimes b)\otimes t]=[a\otimes (b\otimes t)]=[a]\wedge [b\otimes t]=[a]\wedge ([b]\wedge [t])=\alpha \wedge (\beta \wedge \theta ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a92cda22d4dd50698f5df8052dddf5c3c1d9745)
![{\displaystyle (\alpha +\beta )\wedge \theta =([a]+[b])\wedge [t]=[a+b]\wedge [t]=[(a+b)\otimes t]=[a\otimes t+b\otimes t]=[a\otimes t]+[b\otimes t]=[a]\wedge [t]+[b]\wedge [t]=\alpha \wedge \theta +\beta \wedge \theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3731bec5812efe5762122dc15bdbca47fc40a1b4)




























































































