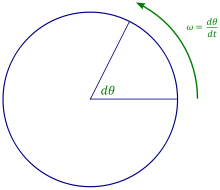
 角速度是用来描述转动的速度以及该转动发生当时的转动轴方向。角速度向量的方向会在转动轴方向上,在本例中(逆时针转动)转动向量是指向读者的。
角速度是用来描述转动的速度以及该转动发生当时的转动轴方向。角速度向量的方向会在转动轴方向上,在本例中(逆时针转动)转动向量是指向读者的。
角速度(Angular velocity)是在物理学中定义为角位移的变化率,描述物体转动时,在单位时间内转过多少角度以及转动方向的向量,(更准确地说,是赝向量),通常用希腊字母 或
或 来表示。
来表示。
在国际单位制中,单位是弧度每秒(rad/s)。在日常生活,通常量度单位时间内的转动周数,即是每分钟转速(rpm),电脑机械硬碟和汽车引擎转数就是以rpm来量度,物理学则以rev/min表示每分钟转动周数。
角速度的方向垂直于转动平面,可通过右手定则来确定,物体以逆时针方向转动其角速度为正值,物体以顺时针方向转动其角速度为负值。
角速度量值的大小称作角速率,通常也是用ω来表示。[1]
 位于
位于 点的质点相对于
点的质点相对于 点的角速度是由其速度向量"
点的角速度是由其速度向量" " 垂直于
" 垂直于 连线的分量来决定 。
连线的分量来决定 。
一个质点在二维平面上的角速度是最基本的。如右图所示,假使从 点向(
点向( )质点画一条直线,则该粒子的速度向量(
)质点画一条直线,则该粒子的速度向量( )可分成在沿著径向上分量(
)可分成在沿著径向上分量( , - 径向分量)以及垂直于径向的分量(
, - 径向分量)以及垂直于径向的分量( - 切线方向分量)。
- 切线方向分量)。
由于粒子在径向上的运动并不会造成相对于原点( )的转动,在求取该粒子的角速度时,可以忽略水平(径向)分量。因此,转动完全是由切线方向的运动所造成的(如同质点在绕著等速率圆周运动),即角速度是完全由垂直(切线方向)的分量所决定的。
质点角度位置的改变率与其切线方向速度的关系式如下:
)的转动,在求取该粒子的角速度时,可以忽略水平(径向)分量。因此,转动完全是由切线方向的运动所造成的(如同质点在绕著等速率圆周运动),即角速度是完全由垂直(切线方向)的分量所决定的。
质点角度位置的改变率与其切线方向速度的关系式如下:

定义角速度为 (其中
(其中 是弧度,即弧长除以半径),而速度的垂直分量
是弧度,即弧长除以半径),而速度的垂直分量 等于
等于 ;其中θ是向量
;其中θ是向量 与
与 的夹角,则导出:
的夹角,则导出:

在二维坐标系中,角速度是一个只有大小没有方向的赝纯量,而非纯量。纯量与赝纯量不同的地方在于,当x 轴与y 轴对调时,纯量不会因此而改变正负符号,然而赝纯量却会因此而改变。角度及角速度则是赝纯量。以一般的定义,从x 轴转向y 轴的方向为转动的正方向。倘若座标轴对调,而物体转动不变,则角度的正负符号将会改变,因此角速度的正负号也跟著改变。
注意:角速度的正负号及数值量取决于原点位置及座标轴方向的选定。
在三维坐标系中,角速度变得比较复杂。在此状况下,角速度通常被当作向量来看待;甚至更精确一点要当作伪向量。它不只具有数值,而且同时具有方向的特性。数值指的是单位时间内的角度变化率,而方向则是用来描述转动轴的。概念上,可以利用右手定则来标示角速度伪向量的正方向。原则如下:
- 假设将右手(除了大拇指以外)的手指顺著转动的方向朝内弯曲,则大拇指所指的方向即是角速度向量的方向。
正如同在二维座标系的例子中,一个质点的移动速度相对于原点可以分成一个沿著径向以及另一个垂直径向的分量。举例而言,原点与质点的速度垂直分量的组合可以定义一个转动平面,质点在此平面上的行为就如同在二维坐标系中的状况下,其转动轴则是一条通过原点且垂直此平面的线,这个轴订定了角速度伪向量的方向,而角速度的数值则是如同在二维座标系状况下求得的伪纯量的值。当定义一个指向角速度伪向量方向单位向量 时,可以用类似二维坐标系的方式来表示角速度:
时,可以用类似二维坐标系的方式来表示角速度:

再加上外积的定义,则可以写成:

一般而言,在高维空间的角速度是一个二阶斜对称的角位移张量对时间的微分。此张量具有 个独立分量,其中"
个独立分量,其中" "这个数字指的是在n-维内积空间中转动李群之李代数的维度。[2]
"这个数字指的是在n-维内积空间中转动李群之李代数的维度。[2]
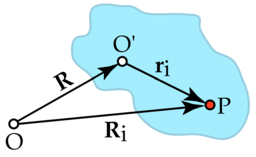
 点在刚体(以蓝色表示)上的位置,
点在刚体(以蓝色表示)上的位置, 是以
是以 为中心在实验室座标系上的位置;而
为中心在实验室座标系上的位置;而 是以
是以 为中心在刚体座标系上的位置。此刚体座标系的原点则是在实验室座标系中的向量位置
为中心在刚体座标系上的位置。此刚体座标系的原点则是在实验室座标系中的向量位置 上。
上。
为了处理刚体运动的问题,最好采用固定在刚体上的座标系统,然后再学习此座标系统与实验室座标系统之间的座标转换。如右图所示, 为实验室座标系统的原点,而
为实验室座标系统的原点,而 是刚体座标系统的原点,
是刚体座标系统的原点, 与
与 之间的向量
之间的向量 。质点(
。质点( )在刚体上
)在刚体上 点的位置上,此质点在实验室座标中的向量位置是
点的位置上,此质点在实验室座标中的向量位置是 ,而在刚体座标中的向量位置为
,而在刚体座标中的向量位置为 。我们可以看到此质点的位置可以写成:
。我们可以看到此质点的位置可以写成:

刚体最重要的特征为任意两点之间距离不随时间变化。这意味着矢量 的长度是不变的。根据欧拉刚体的有限旋转定理,我们可以用
的长度是不变的。根据欧拉刚体的有限旋转定理,我们可以用 来代替
来代替 ,其中
,其中 代表旋转矩阵,而
代表旋转矩阵,而 是初始时刻的质点的位置。这个替代显得非常有意义,随时间变化的只有
是初始时刻的质点的位置。这个替代显得非常有意义,随时间变化的只有 ,而不是相对矢量
,而不是相对矢量 。对于刚体就
。对于刚体就 旋转,质点的位置可以写为:
旋转,质点的位置可以写为:

就质点的速度对时间微分,可以得到质点的速度:

其中 是质点在实验室座标中的速度,而
是质点在实验室座标中的速度,而 是
是 点(刚体座标的原点)的在实验室座标中的速度,故质点的速度可以写成:
点(刚体座标的原点)的在实验室座标中的速度,故质点的速度可以写成:

 是角速度张量,如果我们取角速度张量的对偶,我们即可得到角速度的伪矢量。
是角速度张量,如果我们取角速度张量的对偶,我们即可得到角速度的伪矢量。
![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
而矩阵的乘法可以用外积来取代,导出:

由此可见,刚体中质点的速度可分解成两项—刚体中某固定参考点的速度再加上一项包含该质点相对于此参考点的角速度的外积。相较于 点对于
点对于 点的角速度,这个角速度是“自旋”角速度。
点的角速度,这个角速度是“自旋”角速度。
很重要的是,每个在刚体中的质点具有相同的自转角速度,此自转角速度与刚体上或是实验室座标系统的原点的选择无关。换句话说,这是一个刚体特质所具有的真实物理量,与座标系统的选择无关。然而刚体上的参考点相对于实验室座标原点的角速度则和座标系统的选择有关,为了方便起见,通常选择该刚体的质心当作刚体座标系统的原点,这将大大地简化以数学形式在刚体角动量上的表达。
|
|---|
| 线性(平动)的量 |
|
角度(转动)的量 |
| 量纲 |
— |
L |
L2 |
量纲 |
— |
— |
— |
| T |
时间: t
s |
位移积分: A
m s |
|
T |
时间: t
s |
|
|
| — |
|
距离: d, 位矢: r, s, x, 位移
m |
面积: A
m2 |
— |
|
角度: θ, 角移: θ
rad |
立体角: Ω
rad2, sr |
| T−1 |
频率: f
s−1, Hz |
速率: v, 速度: v
m s−1 |
面积速率: ν
m2 s−1 |
T−1 |
频率: f
s−1, Hz |
角速率: ω, 角速度: ω
rad s−1 |
|
| T−2 |
|
加速度: a
m s−2 |
|
T−2 |
|
角加速度: α
rad s−2 |
|
| T−3 |
|
加加速度: j
m s−3 |
|
T−3 |
|
角加加速度: ζ
rad s−3 |
|
|
|
| M |
质量: m
kg |
|
|
ML2 |
转动惯量: I
kg m2 |
|
|
|---|
| MT−1 |
|
动量: p, 冲量: J
kg m s−1, N s |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
ML2T−1 |
|
角动量: L, 角冲量: ι
kg m2 s−1 |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
| MT−2 |
|
力: F, 重量: Fg
kg m s−2, N |
能量: E, 功: W
kg m2 s−2, J |
ML2T−2 |
|
力矩: τ, moment: M
kg m2 s−2, N m |
能量: E, 功: W
kg m2 s−2, J |
| MT−3 |
|
加力: Y
kg m s−3, N s−1 |
功率: P
kg m2 s−3, W |
ML2T−3 |
|
rotatum: P
kg m2 s−3, N m s−1 |
功率: P
kg m2 s−3, W |
|




































![{\displaystyle {\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f418d52c41570663e22f7b19a8d3a427b69cab)
