摄动
| 航天动力学 |
|---|
 |
摄动是一个天文学术语,用来描述一个大质量天体受到一个以上质量体的引力影响而可察觉的复杂运动[1]。
这种天体的复杂运动可以分成不同的成分而加以描述。首先,假设它的运动只受到一个天体的引力影响,因此它的运动是必然的结果。以其它的方法表示,这种运动可视为二体问题的解,或是为受到摄动的克卜勒轨道。然后,假设上未受到摄动的运动和实际的运动之间的差别,这是由于来自额外的一个或多个物体的引力效应,就是所谓的摄动。如果只有另一个影响较显著的天体,则这种摄动的解称为三体问题;如果有多个物体都有显著的影响,这种运动可以作为更高阶的代表,称为多体问题(N体问题)。
当年,牛顿在导出他的引力运动时,就已经承认摄动的存在,并知道这种计算的复杂和困难[2]。从牛顿的时代开始,已经发展出一些数学上的技术来分析摄动,它们可以分为两大类:一般摄动和特殊摄动。分析一般摄动的方法,运动的常微分方程可以得到解答,通常是一系列的逼近,还有使用三角函数或代数的结果,再使用许多不同的设定,通常就可以得到不同设定条件下的解[3]。从历史上看,一般摄动是先被研究的,因为特殊摄动的方法:数值资料、表示位置的值、速度和加速度的影响,是建立在微分方程数值积分的基础上。
许多系统都涉及多体引力,存在于其中的一个物体是占有引力优势的主导者(例如,恒星系,在这样的案例中是恒星和它的行星;或是行星系,在这样的案例中是行星和它的卫星)。然后,其它的引力影响,相较于未受摄动的行星,可被视为导致行星受到摄动;或是,卫星,各自环绕著主要的天体。
在太阳系,许多的摄动是由周期性的元件造成的,所以摄动的天体依照轨道的周期性或准周期的,长时间的周期-像是月球在它的强扰动轨道,这是月球运动说的主题。
行星会在其它行星的轨道导致周期性的摄动,天王星的轨道受道摄动的结果,导致1846年的发现海王星。
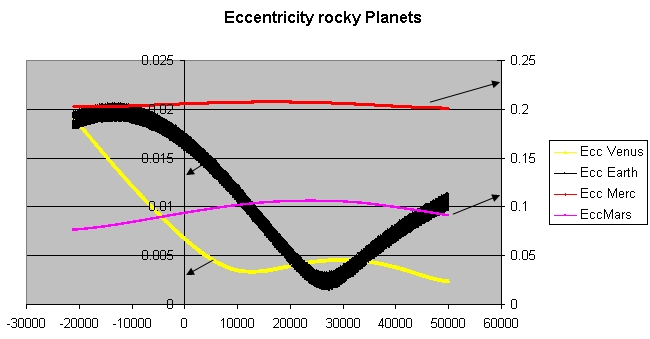
行星相互间的摄动会导致其轨道要素长期的准周期变化。金星目前有著最小的离心率,也就是说它的轨道是行星轨道中最接近圆形的。再过约25,000年,地球的轨道将会比金星的更圆(低离心率)。
太阳系内许多小天体的轨道,像是彗星,经常会受到巨大的摄动,尤其是通过气体巨星的引力场时。虽然这些摄动有很多是周期性的,但也有些不是,并且这些特别可能代表著混沌运动。例如在1996年4月,木星的引力场影响到海尔-博普彗星轨道的周期从4,206年缩减为2,380年,并且这些变化将不会在任何的周期基础上被还原[4]。
在太空动力学和人造卫星的事件中,轨道的摄动通常来自大气拖曳和太阳辐射压力。
相关条目
[编辑]参考资料
[编辑]- ^ Roger R. Bate, Donald D. Mueller, Jerry E. White, "Fundamentals of astrodynamics"(Dover Publications, 1971), e.g. at ch.9, p.385.
- ^ 牛顿在1684年写道:"By reason of the deviation of the Sun from the center of gravity, the centripetal force does not always tend to that immobile center, and hence the planets neither move exactly in ellipses nor revolve twice in the same orbit. Each time a planet revolves it traces a fresh orbit, as in the motion of the Moon, and each orbit depends on the combined motions of all the planets, not to mention the action of all these on each other. But to consider simultaneously all these causes of motion and to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind."(quoted by Prof G E Smith (Tufts University), in "Three Lectures on the Role of Theory in Science"[永久失效链接] 1. Closing the loop: Testing Newtonian Gravity, Then and Now); and Prof R F Egerton(Portland State University, Oregon)after quoting the same passage from Newton concluded: "Here, Newton identifies the "many body problem" which remains unsolved analytically." (页面存档备份,存于互联网档案馆)
- ^ Roger R. Bate, Donald D. Mueller, Jerry E. White, "Fundamentals of astrodynamics"(Dover Publications, 1971), e.g. at p.387 and at section 9.4.3, p.410.
- ^ Don Yeomans. Comet Hale-Bopp Orbit and Ephemeris Information. JPL/NASA. 1997-04-10 [2008-10-23]. (原始内容存档于2011-08-20).
