递归最小二乘滤波器 (RLS)属于自适应滤波器 ,会针对和输入信号有关的加权最小二乘 损失函数 ,递归查找可以使其最小化的系数。此方法和想要减少均方误差 的最小均方滤波器 (LMS)不同。在推导递归最小二乘滤波器时,会假设输入信号是确定性 的,而最小均方滤波及其他算法会假设信号随机
递归最小二乘滤波器是由卡尔·弗里德里希·高斯 发现,但被遗忘无人使用,直到Plackett在1950年发现高斯1821年的著作之后,才再获使用。一般来说,递归最小二乘滤波器可以求得任何可以用自适应滤波器 求解的问题。例如,假设信号
d
(
n
)
{\displaystyle d(n)}
有噪信道 传输,接收到的是
x
(
n
)
=
∑
k
=
0
q
b
n
(
k
)
d
(
n
−
k
)
+
v
(
n
)
{\displaystyle x(n)=\sum _{k=0}^{q}b_{n}(k)d(n-k)+v(n)}
其中
v
(
n
)
{\displaystyle v(n)}
加性高斯白噪声 。RLS滤波器的目的是用
p
+
1
{\displaystyle p+1}
有限冲激响应 (FIR)滤波器
w
{\displaystyle \mathbf {w} }
d
(
n
)
{\displaystyle d(n)}
d
(
n
)
≈
∑
k
=
0
p
w
(
k
)
x
(
n
−
k
)
=
w
T
x
n
{\displaystyle d(n)\approx \sum _{k=0}^{p}w(k)x(n-k)=\mathbf {w} ^{\mathit {T}}\mathbf {x} _{n}}
其中
x
n
=
[
x
(
n
)
x
(
n
−
1
)
…
x
(
n
−
p
)
]
T
{\displaystyle \mathbf {x} _{n}=[x(n)\quad x(n-1)\quad \ldots \quad x(n-p)]^{T}}
x
(
n
)
{\displaystyle x(n)}
p
+
1
{\displaystyle p+1}
列向量 。接收到想要信号的估测值为
d
^
(
n
)
=
∑
k
=
0
p
w
n
(
k
)
x
(
n
−
k
)
=
w
n
T
x
n
{\displaystyle {\hat {d}}(n)=\sum _{k=0}^{p}w_{n}(k)x(n-k)=\mathbf {w} _{n}^{\mathit {T}}\mathbf {x} _{n}}
其目的是估测滤波器
w
{\displaystyle \mathbf {w} }
n
{\displaystyle n}
w
n
{\displaystyle \mathbf {w} _{n}}
w
n
+
1
{\displaystyle \mathbf {w} _{n+1}}
w
n
{\displaystyle \mathbf {w} _{n}}
转置
w
n
T
{\displaystyle \mathbf {w} _{n}^{\mathit {T}}}
矩阵乘法
w
n
T
x
n
{\displaystyle \mathbf {w} _{n}^{\mathit {T}}\mathbf {x} _{n}}
w
n
{\displaystyle \mathbf {w} _{n}}
x
n
{\displaystyle \mathbf {x} _{n}}
点积 )是
d
^
(
n
)
{\displaystyle {\hat {d}}(n)}
d
^
(
n
)
−
d
(
n
)
{\displaystyle {\hat {d}}(n)-d(n)}
最小二乘法 的概念下,其值是小的,其估测就算是好的。
随着时间演进,会希望避免完全重做最小方差算法来找新估测值
w
n
+
1
{\displaystyle \mathbf {w} _{n+1}}
w
n
+
1
{\displaystyle \mathbf {w} _{n+1}}
w
n
{\displaystyle \mathbf {w} _{n}}
递归最小二乘滤波器的好处是不用进行反矩阵运算,因此可以节省计算时间。另一个好处是在其结果之后,提供了类似卡尔曼滤波 的直觉信息。
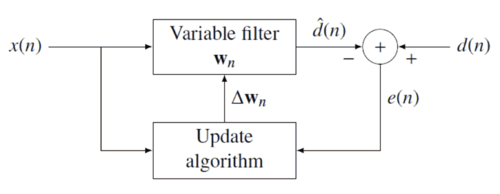
递归最小二乘滤波器背后的概念是在收到新资料时,适当选择滤波器系数
w
n
{\displaystyle \mathbf {w} _{n}}
损失函数
C
{\displaystyle C}
e
(
n
)
{\displaystyle e(n)}
d
(
n
)
{\displaystyle d(n)}
负反馈 框图来说明:
误差会透过估测值
d
^
(
n
)
{\displaystyle {\hat {d}}(n)}
e
(
n
)
=
d
(
n
)
−
d
^
(
n
)
{\displaystyle e(n)=d(n)-{\hat {d}}(n)}
加权最小方差函数
C
{\displaystyle C}
e
(
n
)
{\displaystyle e(n)}
C
(
w
n
)
=
∑
i
=
0
n
λ
n
−
i
e
2
(
i
)
{\displaystyle C(\mathbf {w} _{n})=\sum _{i=0}^{n}\lambda ^{n-i}e^{2}(i)}
其中
0
<
λ
≤
1
{\displaystyle 0<\lambda \leq 1}
费用函数最小化的方式,是将系数向量
w
n
{\displaystyle \mathbf {w} _{n}}
∂
C
(
w
n
)
∂
w
n
(
k
)
=
∑
i
=
0
n
2
λ
n
−
i
e
(
i
)
⋅
∂
e
(
i
)
∂
w
n
(
k
)
=
−
∑
i
=
0
n
2
λ
n
−
i
e
(
i
)
x
(
i
−
k
)
=
0
k
=
0
,
1
,
…
,
p
{\displaystyle {\frac {\partial C(\mathbf {w} _{n})}{\partial w_{n}(k)}}=\sum _{i=0}^{n}2\lambda ^{n-i}e(i)\cdot {\frac {\partial e(i)}{\partial w_{n}(k)}}=-\sum _{i=0}^{n}2\lambda ^{n-i}e(i)\,x(i-k)=0\qquad k=0,1,\ldots ,p}
接着,用以下的误差信号来代替
e
(
n
)
{\displaystyle e(n)}
∑
i
=
0
n
λ
n
−
i
[
d
(
i
)
−
∑
ℓ
=
0
p
w
n
(
ℓ
)
x
(
i
−
ℓ
)
]
x
(
i
−
k
)
=
0
k
=
0
,
1
,
…
,
p
{\displaystyle \sum _{i=0}^{n}\lambda ^{n-i}\left[d(i)-\sum _{\ell =0}^{p}w_{n}(\ell )x(i-\ell )\right]x(i-k)=0\qquad k=0,1,\ldots ,p}
将等式重组如下
∑
ℓ
=
0
p
w
n
(
ℓ
)
[
∑
i
=
0
n
λ
n
−
i
x
(
i
−
ℓ
)
x
(
i
−
k
)
]
=
∑
i
=
0
n
λ
n
−
i
d
(
i
)
x
(
i
−
k
)
k
=
0
,
1
,
…
,
p
{\displaystyle \sum _{\ell =0}^{p}w_{n}(\ell )\left[\sum _{i=0}^{n}\lambda ^{n-i}\,x(i-\ell )x(i-k)\right]=\sum _{i=0}^{n}\lambda ^{n-i}d(i)x(i-k)\qquad k=0,1,\ldots ,p}
可以表示为以下的矩阵
R
x
(
n
)
w
n
=
r
d
x
(
n
)
{\displaystyle \mathbf {R} _{x}(n)\,\mathbf {w} _{n}=\mathbf {r} _{dx}(n)}
其中
R
x
(
n
)
{\displaystyle \mathbf {R} _{x}(n)}
x
(
n
)
{\displaystyle x(n)}
样本协方差
r
d
x
(
n
)
{\displaystyle \mathbf {r} _{dx}(n)}
d
(
n
)
{\displaystyle d(n)}
x
(
n
)
{\displaystyle x(n)}
互协方差 的等效估计。依照上式可以找到最小化费用函数的系数
w
n
=
R
x
−
1
(
n
)
r
d
x
(
n
)
{\displaystyle \mathbf {w} _{n}=\mathbf {R} _{x}^{-1}(n)\,\mathbf {r} _{dx}(n)}
λ
{\displaystyle \lambda }
λ
=
1
{\displaystyle \lambda =1}
λ
{\displaystyle \lambda }
[ 1]
λ
{\displaystyle \lambda }
[ 2]
以上叙述的结论是可以决定费用函数的参数,使费用函数最小化的方程式。以下则说明如何找到此形式的递归解
w
n
=
w
n
−
1
+
Δ
w
n
−
1
{\displaystyle \mathbf {w} _{n}=\mathbf {w} _{n-1}+\Delta \mathbf {w} _{n-1}}
其中
Δ
w
n
−
1
{\displaystyle \Delta \mathbf {w} _{n-1}}
n
−
1
{\displaystyle {n-1}}
r
d
x
(
n
)
{\displaystyle \mathbf {r} _{dx}(n)}
r
d
x
(
n
−
1
)
{\displaystyle \mathbf {r} _{dx}(n-1)}
r
d
x
(
n
)
{\displaystyle \mathbf {r} _{dx}(n)}
=
∑
i
=
0
n
λ
n
−
i
d
(
i
)
x
(
i
)
{\displaystyle =\sum _{i=0}^{n}\lambda ^{n-i}d(i)\mathbf {x} (i)}
=
∑
i
=
0
n
−
1
λ
n
−
i
d
(
i
)
x
(
i
)
+
λ
0
d
(
n
)
x
(
n
)
{\displaystyle =\sum _{i=0}^{n-1}\lambda ^{n-i}d(i)\mathbf {x} (i)+\lambda ^{0}d(n)\mathbf {x} (n)}
=
λ
r
d
x
(
n
−
1
)
+
d
(
n
)
x
(
n
)
{\displaystyle =\lambda \mathbf {r} _{dx}(n-1)+d(n)\mathbf {x} (n)}
其中
x
(
i
)
{\displaystyle \mathbf {x} (i)}
p
+
1
{\displaystyle {p+1}}
x
(
i
)
=
[
x
(
i
)
,
x
(
i
−
1
)
,
…
,
x
(
i
−
p
)
]
T
{\displaystyle \mathbf {x} (i)=[x(i),x(i-1),\dots ,x(i-p)]^{T}}
接下来以相似的方式,用
R
x
(
n
−
1
)
{\displaystyle \mathbf {R} _{x}(n-1)}
R
x
(
n
)
{\displaystyle \mathbf {R} _{x}(n)}
R
x
(
n
)
{\displaystyle \mathbf {R} _{x}(n)}
=
∑
i
=
0
n
λ
n
−
i
x
(
i
)
x
T
(
i
)
{\displaystyle =\sum _{i=0}^{n}\lambda ^{n-i}\mathbf {x} (i)\mathbf {x} ^{T}(i)}
=
λ
R
x
(
n
−
1
)
+
x
(
n
)
x
T
(
n
)
{\displaystyle =\lambda \mathbf {R} _{x}(n-1)+\mathbf {x} (n)\mathbf {x} ^{T}(n)}
为了要找到其系数向量,接下来要关注的是决定性自协方差矩阵的反矩阵。这问题可以使用伍德伯里矩阵恒等式
A
{\displaystyle A}
=
λ
R
x
(
n
−
1
)
{\displaystyle =\lambda \mathbf {R} _{x}(n-1)}
(
p
+
1
)
×
(
p
+
1
)
{\displaystyle (p+1)\times (p+1)}
U
{\displaystyle U}
=
x
(
n
)
{\displaystyle =\mathbf {x} (n)}
(
p
+
1
)
×
1
{\displaystyle (p+1)\times 1}
V
{\displaystyle V}
=
x
T
(
n
)
{\displaystyle =\mathbf {x} ^{T}(n)}
1
×
(
p
+
1
)
{\displaystyle 1\times (p+1)}
C
{\displaystyle C}
=
I
1
{\displaystyle =\mathbf {I} _{1}}
1
×
1
{\displaystyle 1\times 1}
单位矩阵
依照伍德伯里矩阵恒等式,可得到下式
R
x
−
1
(
n
)
{\displaystyle \mathbf {R} _{x}^{-1}(n)}
=
{\displaystyle =}
[
λ
R
x
(
n
−
1
)
+
x
(
n
)
x
T
(
n
)
]
−
1
{\displaystyle \left[\lambda \mathbf {R} _{x}(n-1)+\mathbf {x} (n)\mathbf {x} ^{T}(n)\right]^{-1}}
=
{\displaystyle =}
1
λ
{
R
x
−
1
(
n
−
1
)
−
R
x
−
1
(
n
−
1
)
x
(
n
)
x
T
(
n
)
R
x
−
1
(
n
−
1
)
λ
+
x
T
(
n
)
R
x
−
1
(
n
−
1
)
x
(
n
)
}
{\displaystyle {\dfrac {1}{\lambda }}\left\lbrace \mathbf {R} _{x}^{-1}(n-1)-{\dfrac {\mathbf {R} _{x}^{-1}(n-1)\mathbf {x} (n)\mathbf {x} ^{T}(n)\mathbf {R} _{x}^{-1}(n-1)}{\lambda +\mathbf {x} ^{T}(n)\mathbf {R} _{x}^{-1}(n-1)\mathbf {x} (n)}}\right\rbrace }
{\displaystyle }
为了和标准的文献一致,定义
P
(
n
)
{\displaystyle \mathbf {P} (n)}
=
R
x
−
1
(
n
)
{\displaystyle =\mathbf {R} _{x}^{-1}(n)}
=
λ
−
1
P
(
n
−
1
)
−
g
(
n
)
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
{\displaystyle =\lambda ^{-1}\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)}
其中的增益向量
g
(
n
)
{\displaystyle g(n)}
g
(
n
)
{\displaystyle \mathbf {g} (n)}
=
λ
−
1
P
(
n
−
1
)
x
(
n
)
{
1
+
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
x
(
n
)
}
−
1
{\displaystyle =\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)\left\{1+\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)\right\}^{-1}}
=
P
(
n
−
1
)
x
(
n
)
{
λ
+
x
T
(
n
)
P
(
n
−
1
)
x
(
n
)
}
−
1
{\displaystyle =\mathbf {P} (n-1)\mathbf {x} (n)\left\{\lambda +\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {x} (n)\right\}^{-1}}
在往下推导之前,需要将
g
(
n
)
{\displaystyle \mathbf {g} (n)}
g
(
n
)
{
1
+
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
x
(
n
)
}
{\displaystyle \mathbf {g} (n)\left\{1+\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)\right\}}
=
λ
−
1
P
(
n
−
1
)
x
(
n
)
{\displaystyle =\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)}
g
(
n
)
+
g
(
n
)
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
x
(
n
)
{\displaystyle \mathbf {g} (n)+\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)}
=
λ
−
1
P
(
n
−
1
)
x
(
n
)
{\displaystyle =\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)}
等式两侧减去左边的第二项,得到
g
(
n
)
{\displaystyle \mathbf {g} (n)}
=
λ
−
1
P
(
n
−
1
)
x
(
n
)
−
g
(
n
)
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
x
(
n
)
{\displaystyle =\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\mathbf {x} (n)}
=
λ
−
1
[
P
(
n
−
1
)
−
g
(
n
)
x
T
(
n
)
P
(
n
−
1
)
]
x
(
n
)
{\displaystyle =\lambda ^{-1}\left[\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\right]\mathbf {x} (n)}
配合
P
(
n
)
{\displaystyle \mathbf {P} (n)}
g
(
n
)
=
P
(
n
)
x
(
n
)
{\displaystyle \mathbf {g} (n)=\mathbf {P} (n)\mathbf {x} (n)}
此时就可以完成递归,如以上讨论
w
n
{\displaystyle \mathbf {w} _{n}}
=
P
(
n
)
r
d
x
(
n
)
{\displaystyle =\mathbf {P} (n)\,\mathbf {r} _{dx}(n)}
=
λ
P
(
n
)
r
d
x
(
n
−
1
)
+
d
(
n
)
P
(
n
)
x
(
n
)
{\displaystyle =\lambda \mathbf {P} (n)\,\mathbf {r} _{dx}(n-1)+d(n)\mathbf {P} (n)\,\mathbf {x} (n)}
第二步是从
r
d
x
(
n
)
{\displaystyle \mathbf {r} _{dx}(n)}
P
(
n
)
{\displaystyle \mathbf {P} (n)}
g
(
n
)
{\displaystyle \mathbf {g} (n)}
w
n
{\displaystyle \mathbf {w} _{n}}
=
λ
[
λ
−
1
P
(
n
−
1
)
−
g
(
n
)
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
]
r
d
x
(
n
−
1
)
+
d
(
n
)
g
(
n
)
{\displaystyle =\lambda \left[\lambda ^{-1}\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\right]\mathbf {r} _{dx}(n-1)+d(n)\mathbf {g} (n)}
=
P
(
n
−
1
)
r
d
x
(
n
−
1
)
−
g
(
n
)
x
T
(
n
)
P
(
n
−
1
)
r
d
x
(
n
−
1
)
+
d
(
n
)
g
(
n
)
{\displaystyle =\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)+d(n)\mathbf {g} (n)}
=
P
(
n
−
1
)
r
d
x
(
n
−
1
)
+
g
(
n
)
[
d
(
n
)
−
x
T
(
n
)
P
(
n
−
1
)
r
d
x
(
n
−
1
)
]
{\displaystyle =\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)+\mathbf {g} (n)\left[d(n)-\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)\right]}
配合
w
n
−
1
=
P
(
n
−
1
)
r
d
x
(
n
−
1
)
{\displaystyle \mathbf {w} _{n-1}=\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)}
w
n
{\displaystyle \mathbf {w} _{n}}
=
w
n
−
1
+
g
(
n
)
[
d
(
n
)
−
x
T
(
n
)
w
n
−
1
]
{\displaystyle =\mathbf {w} _{n-1}+\mathbf {g} (n)\left[d(n)-\mathbf {x} ^{T}(n)\mathbf {w} _{n-1}\right]}
=
w
n
−
1
+
g
(
n
)
α
(
n
)
{\displaystyle =\mathbf {w} _{n-1}+\mathbf {g} (n)\alpha (n)}
其中
α
(
n
)
=
d
(
n
)
−
x
T
(
n
)
w
n
−
1
{\displaystyle \alpha (n)=d(n)-\mathbf {x} ^{T}(n)\mathbf {w} _{n-1}}
先验 误差。将此和后验误差(在滤波器更新后计算的误差)比较
e
(
n
)
=
d
(
n
)
−
x
T
(
n
)
w
n
{\displaystyle e(n)=d(n)-\mathbf {x} ^{T}(n)\mathbf {w} _{n}}
这就找到了修正因子
Δ
w
n
−
1
=
g
(
n
)
α
(
n
)
{\displaystyle \Delta \mathbf {w} _{n-1}=\mathbf {g} (n)\alpha (n)}
这个结论指出了修正系数直接和误差和增益向量成正比,增益向量会透过加权因子
λ
{\displaystyle \lambda }
p 阶RLS滤波器的算法可以摘要如下
参数:
p
=
{\displaystyle p=}
λ
=
{\displaystyle \lambda =}
δ
=
P
(
0
)
{\displaystyle \delta =\mathbf {P} (0)}
开始:
w
(
0
)
=
0
{\displaystyle \mathbf {w} (0)=0}
x
(
k
)
=
0
,
k
=
−
p
,
…
,
−
1
{\displaystyle x(k)=0,k=-p,\dots ,-1}
d
(
k
)
=
0
,
k
=
−
p
,
…
,
−
1
{\displaystyle d(k)=0,k=-p,\dots ,-1}
P
(
0
)
=
δ
I
{\displaystyle \mathbf {P} (0)=\delta I}
I
{\displaystyle I}
p
+
1
{\displaystyle p+1}
单位矩阵
计算:
针对
n
=
1
,
2
,
…
{\displaystyle n=1,2,\dots }
x
(
n
)
=
[
x
(
n
)
x
(
n
−
1
)
⋮
x
(
n
−
p
)
]
{\displaystyle \mathbf {x} (n)=\left[{\begin{matrix}x(n)\\x(n-1)\\\vdots \\x(n-p)\end{matrix}}\right]}
α
(
n
)
=
d
(
n
)
−
x
T
(
n
)
w
(
n
−
1
)
{\displaystyle \alpha (n)=d(n)-\mathbf {x} ^{T}(n)\mathbf {w} (n-1)}
g
(
n
)
=
P
(
n
−
1
)
x
(
n
)
{
λ
+
x
T
(
n
)
P
(
n
−
1
)
x
(
n
)
}
−
1
{\displaystyle \mathbf {g} (n)=\mathbf {P} (n-1)\mathbf {x} (n)\left\{\lambda +\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {x} (n)\right\}^{-1}}
P
(
n
)
=
λ
−
1
P
(
n
−
1
)
−
g
(
n
)
x
T
(
n
)
λ
−
1
P
(
n
−
1
)
{\displaystyle \mathbf {P} (n)=\lambda ^{-1}\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)}
w
(
n
)
=
w
(
n
−
1
)
+
α
(
n
)
g
(
n
)
{\displaystyle \mathbf {w} (n)=\mathbf {w} (n-1)+\,\alpha (n)\mathbf {g} (n)}
P
{\displaystyle P}
代数Riccati方程 ,也类似卡尔曼滤波 的结果[ 3]
^ Emannual C. Ifeacor, Barrie W. Jervis. Digital signal processing: a practical approach, second edition. Indianapolis: Pearson Education Limited, 2002, p. 718
^ Steven Van Vaerenbergh, Ignacio Santamaría, Miguel Lázaro-Gredilla "Estimation of the forgetting factor in kernel recursive least squares" , 2012 IEEE International Workshop on Machine Learning for Signal Processing, 2012, accessed June 23, 2016.
^ Welch, Greg and Bishop, Gary "An Introduction to the Kalman Filter" , Department of Computer Science, University of North Carolina at Chapel Hill, September 17, 1997, accessed July 19, 2011.
Hayes, Monson H. 9.4: Recursive Least Squares. Statistical Digital Signal Processing and Modeling. Wiley. 1996: 541. ISBN 0-471-59431-8 Simon Haykin, Adaptive Filter Theory , Prentice Hall, 2002, ISBN 0-13-048434-2
M.H.A Davis, R.B. Vinter, Stochastic Modelling and Control , Springer, 1985, ISBN 0-412-16200-8
Weifeng Liu, Jose Principe and Simon Haykin, Kernel Adaptive Filtering: A Comprehensive Introduction , John Wiley, 2010, ISBN 0-470-44753-2
R.L.Plackett, Some Theorems in Least Squares , Biometrika, 1950, 37, 149–157, ISSN 0006-3444
C.F.Gauss, Theoria combinationis observationum erroribus minimis obnoxiae , 1821, Werke, 4. Gottinge 






![{\displaystyle \mathbf {x} _{n}=[x(n)\quad x(n-1)\quad \ldots \quad x(n-p)]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09eb921b307dabe5f3f396085912215d09c02114)
















![{\displaystyle \sum _{i=0}^{n}\lambda ^{n-i}\left[d(i)-\sum _{\ell =0}^{p}w_{n}(\ell )x(i-\ell )\right]x(i-k)=0\qquad k=0,1,\ldots ,p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19ddcbc3bdad707cdb76a5d5371bc1bee9872174)
![{\displaystyle \sum _{\ell =0}^{p}w_{n}(\ell )\left[\sum _{i=0}^{n}\lambda ^{n-i}\,x(i-\ell )x(i-k)\right]=\sum _{i=0}^{n}\lambda ^{n-i}d(i)x(i-k)\qquad k=0,1,\ldots ,p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5289d4da73b7a149fdf9a53cbd8c80a11c0dfe6)















![{\displaystyle \mathbf {x} (i)=[x(i),x(i-1),\dots ,x(i-p)]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dab2ea44a54d82de74ac9f6d26e3f5f6c2a44d8a)
















![{\displaystyle \left[\lambda \mathbf {R} _{x}(n-1)+\mathbf {x} (n)\mathbf {x} ^{T}(n)\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f12c798517a6c530e616e5915429e3e16370785e)













![{\displaystyle =\lambda ^{-1}\left[\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\right]\mathbf {x} (n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3baaff4ae27f9cfc51e54ada85a9de0999978262)



![{\displaystyle =\lambda \left[\lambda ^{-1}\mathbf {P} (n-1)-\mathbf {g} (n)\mathbf {x} ^{T}(n)\lambda ^{-1}\mathbf {P} (n-1)\right]\mathbf {r} _{dx}(n-1)+d(n)\mathbf {g} (n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1dfdfb80807912183bd47c28d76f65ea9d4c553)

![{\displaystyle =\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)+\mathbf {g} (n)\left[d(n)-\mathbf {x} ^{T}(n)\mathbf {P} (n-1)\mathbf {r} _{dx}(n-1)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9800c914543c33d7b8ebd7f295efc9fdc51b57e7)

![{\displaystyle =\mathbf {w} _{n-1}+\mathbf {g} (n)\left[d(n)-\mathbf {x} ^{T}(n)\mathbf {w} _{n-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78ebe76268d69116b2d676aab45f0272977a6df2)













![{\displaystyle \mathbf {x} (n)=\left[{\begin{matrix}x(n)\\x(n-1)\\\vdots \\x(n-p)\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85a8706d78172d40a299b2bb60ae26b22a21f6c)




