在极点为O、极轴为L的极坐标系里,点(3, 60°)的径向坐标为3、角坐标为60°,点(4, 210°)的径向坐标为4、角坐标为210°。 在数学 中,极坐标系 (英语:polar coordinate system )是一个二维 坐标系统 。该坐标系统中任意位置可由一个夹角 和一段相对原点 —极点的距离 来表示。极坐标系的应用领域十分广泛,包括数学 、物理 、工程 、航海 、航空 、电脑 以及机器人 领域。在两点间的关系用夹角和距离很容易表示时,极坐标系便显得尤为有用;而在平面直角坐标系中,这样的关系就只能使用三角函数 来表示。对于很多类型的曲线,极坐标方程是最简单的表达形式,甚至对于某些曲线来说,只有极坐标方程能够表示。
希腊人 最早使用了角度和弧度的概念。天文学家喜帕恰斯 (190-120 BC)制成了一张求各角所对弦 的弦长函数的表格。并且,曾有人引用了他的极坐标系来确定恒星位置。在螺线方面,阿基米德 描述了他的著名的螺线,一个半径随角度变化的方程。希腊人作出了贡献,尽管最终并没有建立整个坐标系统。
关于是谁首次将极坐标系应用为一个正式的坐标系统,流传着有多种观点。关于这一问题的较详尽历史,哈佛大学 教授朱利安·科利奇 (Julian Coolidge )的《极坐标系起源》[ 1] [ 2] 格雷瓜·德·圣-万桑特 (Grégoire de Saint-Vincent )和博纳文图拉·卡瓦列里 ,被认为在几乎同时、并独立地各自引入了极坐标系这一概念。圣-万桑特在1625年的私人文稿中进行了论述并发表于1647年,而卡瓦列里在1635进行了发表,而后又于1653年进行了更正。卡瓦列里首次利用极坐标系来解决一个关于阿基米德螺线 内的面积问题。布莱士·帕斯卡 随后使用极坐标系来计算抛物线 的长度。
在1671年写成,1736年出版的《流数术和无穷级数》(Method of Fluxions )一书中,艾萨克·牛顿 第一个将极坐标系应用于表示平面上的任何一点。牛顿在书中验证了极坐标和其他九种坐标系的变换关系。在1691年出版的《博学通报》(Acta eruditorum ,Acta eruditorum )一书中雅各布·伯努利 正式使用定点和从定点引出的一条射线,定点称为极点,射线称为极轴。平面内任何一点的坐标都通过该点与定点的距离和与极轴的夹角来表示。伯努利通过极坐标系对曲线的曲率半径进行了研究。
实际上应用“极坐标”(polar coordinate system )这个术语的是由格雷古廖·丰塔纳 (Gregorio Fontana )开始的,并且被18世纪的意大利数学家所使用。该术语是由乔治·皮科克 (George Peacock )在1816年翻译席维斯·拉克鲁克斯 (Sylvestre François Lacroix )的《微分学与积分学》(Traité du calcul différentiel et du calcul intégral )[ 3] [ 4] [ 5]
亚历克西斯·克莱罗 和莱昂哈德·欧拉 被认为是将平面极坐标系扩展到三维空间的数学家。
正如所有的二维坐标系,极坐标系也有两个坐标轴:
r
{\displaystyle r}
θ
{\displaystyle \theta }
方位角 ,有时也表示为
ϕ
{\displaystyle \phi }
t
{\displaystyle t}
r
{\displaystyle r}
θ
{\displaystyle \theta }
射线 (有时也称作极轴)的角度,极轴就是在平面直角坐标系 中的x轴正方向。[ 6]
比如,极坐标中的(3, 60°)表示了一个距离极点3个单位长度、和极轴夹角为60°的点。(−3, 240°)和(3, 60°)表示了同一点,因为该点的半径为在夹角射线反向延长线上距离极点3个单位长度的地方(240° − 180° = 60°)。
极坐标系中一个重要的特性是,平面直角坐标中的任意一点,可以在极坐标系中有无限种表达形式。通常来说,点(r, θ)可以任意表示为(r , θ ± n ×360°)或(−r , θ ± (2n + 1)180°),这里n 是任意整数。[ 7] r 坐标为0,那么无论θ取何值,该点的位置都落在了极点上。
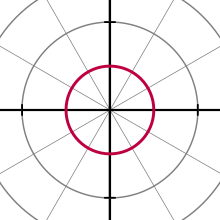
每隔30°标记一次角度的极坐标网格。 极坐标系中的角度通常表示为角度或者弧度 ,使用公式2π rad= 360°。具体使用哪一种方式,基本都是由使用场合而定。航海 方面经常使用角度来进行测量,而物理 学的某些领域大量使用到了半径和圆周的比来作运算,所以物理方面更倾向使用弧度。[ 8]
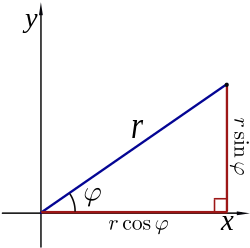
极坐标与直角坐标之间的关系。 从极坐标
r
{\displaystyle r}
θ
{\displaystyle \theta }
直角坐标 :
r
=
y
2
+
x
2
{\displaystyle r={\sqrt {y^{2}+x^{2}}}\quad }
勾股定理 )
θ
=
atan2
(
y
,
x
)
{\displaystyle \theta =\operatorname {atan2} (y,x)\quad }
atan2 是已将象限 纳入考量的反正切 函数)或
θ
=
{
arctan
(
y
x
)
if
x
>
0
arctan
(
y
x
)
+
π
if
x
<
0
and
y
≥
0
arctan
(
y
x
)
−
π
if
x
<
0
and
y
<
0
π
2
if
x
=
0
and
y
>
0
−
π
2
if
x
=
0
and
y
<
0
0
if
x
=
0
and
y
=
0
{\displaystyle \theta ={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0\\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ and }}y<0\\{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0\\0&{\text{if }}x=0{\text{ and }}y=0\end{cases}}}
从直角坐标
x
{\displaystyle x}
y
{\displaystyle y}
x
=
r
cos
θ
{\displaystyle x=r\cos \theta }
y
=
r
sin
θ
{\displaystyle y=r\sin \theta }
这方程式给出
θ
{\displaystyle \theta }
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
[ 9]
(
−
180
∘
,
180
∘
]
{\displaystyle (-180^{\circ },180^{\circ }]}
(
0
,
0
)
{\displaystyle (0,0)}
+
π
/
2
{\displaystyle +\pi /2}
+
90
∘
{\displaystyle +90^{\circ }}
大多数常用编程语言会特别设定一个函数,专门从
x
{\displaystyle x}
y
{\displaystyle y}
θ
{\displaystyle \theta }
C语言 里,这函数标记为atan2(y,x),在Common Lisp 里,标记为(atan y x)。对于这两种案例,计算结果是在值域
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
θ
{\displaystyle \theta }
辐角 的主值 (principal value),注意到当
x
{\displaystyle x}
y
{\displaystyle y}
假若需要,将角坐标
θ
{\displaystyle \theta }
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
π
{\displaystyle \pi }
[
0
,
2
π
)
{\displaystyle [0,2\pi )}
函数:用极坐标系描述的曲线 方程称作极坐标方程 ,通常表示为r 为自变量θ的函数 。 对称:极坐标方程经常会表现出不同的对称 形式,如果r (−θ) = r (θ),则曲线关于极点(0°/180°)对称,如果r(π−θ) = r(θ),则曲线关于极点(90°/270°)对称,如果r(θ−α) = r(θ),则曲线相当于从极点逆时针方向 旋转 α°。 方程为
r
(
θ
)
=
1
{\displaystyle r(\theta )=1}
圆 。 在极坐标系中,圆心在(r 0 ,
φ
{\displaystyle \varphi }
a 的圆的一般方程为
r
2
−
2
r
r
0
cos
(
θ
−
φ
)
+
r
0
2
=
a
2
{\displaystyle r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}}
特定情况:比如方程
r
(
θ
)
=
a
{\displaystyle r(\theta )=a}
表示一个以极点为中心半径为a 的圆。[ 10]
设圆的半径为
r
{\displaystyle r}
(
p
0
,
α
)
{\displaystyle (p_{0},\alpha )}
(
p
0
cos
α
,
p
0
sin
α
)
{\displaystyle (p_{0}\cos \alpha ,p_{0}\sin \alpha )}
(
x
−
p
0
cos
α
)
2
+
(
y
−
p
0
sin
α
)
2
=
r
2
{\displaystyle (x-p_{0}\cos \alpha )^{2}+(y-p_{0}\sin \alpha )^{2}=r^{2}}
设圆上的点的极坐标为
(
p
,
β
)
{\displaystyle (p,\beta )}
x
=
p
cos
β
,
y
=
p
sin
β
{\displaystyle x=p\cos \beta ,\qquad y=p\sin \beta }
因此,
p
2
−
2
p
p
0
(
sin
β
sin
α
+
cos
β
cos
α
)
+
p
0
2
=
r
2
{\displaystyle p^{2}-2pp_{0}(\sin \beta \sin \alpha +\cos \beta \cos \alpha )+p_{0}^{2}=r^{2}}
化简为
p
2
+
p
0
2
−
2
p
p
0
cos
(
β
−
α
)
=
r
2
{\displaystyle p^{2}+p_{0}^{2}-2pp_{0}\cos(\beta -\alpha )=r^{2}}
过极点的射线方程:
θ
=
φ
{\displaystyle \theta =\varphi }
其中φ为射线的倾斜角。若m为直角坐标系 的射线的斜率 ,则有φ = arctan m 。任何不经过极点的直线都会与某条射线垂直 。[ 11] r 0 , φ)处的直线与射线θ = φ垂直,其方程为
r
(
θ
)
=
r
0
sec
(
θ
−
φ
)
{\displaystyle r(\theta )={r_{0}}\sec(\theta -\varphi )}
一条方程为r (θ) = 2 sin 4θ的玫瑰线 。 极坐标的玫瑰线(polar rose )是数学曲线中非常著名的曲线,看上去像花瓣,它只能用极坐标方程来描述,方程如下:
r
(
θ
)
=
a
cos
k
θ
{\displaystyle r(\theta )=a\cos k\theta }
r
(
θ
)
=
a
sin
k
θ
{\displaystyle r(\theta )=a\sin k\theta }
如果k 是整数,当k 是奇数时那么曲线将会是k个花瓣,当k 是偶数时曲线将是2k个花瓣。如果k 为非整数,将产生圆盘 状图形,且花瓣数也为非整数。注意:该方程不可能产生4的倍数加2(如2,6,10……)个花瓣。变量a 代表玫瑰线花瓣的长度。
方程r (θ) = θ(0<θ<6π)的一条阿基米德螺线 。 阿基米德螺线 在极坐标里使用以下方程表示:
r
(
θ
)
=
a
+
b
θ
{\displaystyle r(\theta )=a+b\theta }
改变参数a 将改变螺线形状,b 控制螺线间距离,通常其为常量。阿基米德螺线有两条螺线,一条θ>0,另一条θ<0。两条螺线在极点处平滑地连接。把其中一条翻转
90°/270°得到其镜像,就是另一条螺线。
椭圆 ,展示了半正焦弦 圆锥曲线 方程如下:
r
=
ℓ
(
1
−
e
cos
θ
)
{\displaystyle r={\ell \over (1-e\cos \theta )}}
其中
ℓ
{\displaystyle \ell }
半正焦弦 ,e 表示离心率 。
如果e < 1,曲线为椭圆 ,如果e = 1,曲线为抛物线 ,如果e > 1,则表示双曲线 。
r
=
e
p
(
1
−
e
cos
θ
)
{\displaystyle r={ep \over (1-e\cos \theta )}}
其中e 表示离心率 ,p 表示焦点到准线的距离 。
由于坐标系统是基于圆环的,所以许多有关曲线的方程,极坐标要比直角坐标系(笛卡尔形式)简单得多。比如伯努利双纽线 ,蚶线 (limaçon ),还有心脏线 。
复数 的通常矩形 形式为a + bi ,在极坐标中也可以表示为两种不同的方式:
r
(
cos
θ
+
i
sin
θ
)
{\displaystyle r(\cos \theta +i\sin \theta )}
r
cis
θ
{\displaystyle r\operatorname {cis} \theta }
r
e
i
θ
{\displaystyle re^{i\theta }}
等同于欧拉公式 。[ 12]
a
=
r
cos
θ
{\displaystyle a=r\cos \theta }
b
=
r
sin
θ
{\displaystyle b=r\sin \theta }
其中
r
=
a
2
+
b
2
{\displaystyle r={\sqrt {a^{2}+b^{2}}}}
复数的乘法 、除法 以及指数 以及开方运算,在极坐标中会比在直角坐标中容易得多,他们分别是:
乘法:
(
r
cis
θ
)
∗
(
R
cis
φ
)
=
r
R
cis
(
θ
+
φ
)
{\displaystyle (r\operatorname {cis} \theta )*(R\operatorname {cis} \varphi )=rR\operatorname {cis} (\theta +\varphi )}
除法:
r
cis
θ
R
cis
φ
=
r
R
cis
(
θ
−
φ
)
{\displaystyle {\frac {r\operatorname {cis} \theta }{R\operatorname {cis} \varphi }}={\frac {r}{R}}\operatorname {cis} (\theta -\varphi )}
指数(棣莫弗定理 ,De Moivre's formula):
(
r
cis
θ
)
n
=
r
n
cis
(
n
θ
)
{\displaystyle (r\operatorname {cis} \theta )^{n}=r^{n}\operatorname {cis} (n\theta )}
微积分 可适用于极坐标系下表达的等式。[ 13] [ 14]
利用x = r cos θ y = r sin θ u (x ,y ),通过计算其全微分 可得:
r
∂
u
∂
r
=
r
∂
u
∂
x
∂
x
∂
r
+
r
∂
u
∂
y
∂
y
∂
r
,
∂
u
∂
θ
=
∂
u
∂
x
∂
x
∂
θ
+
∂
u
∂
y
∂
y
∂
θ
,
{\displaystyle {\begin{aligned}r{\frac {\partial u}{\partial r}}&=r{\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial r}}+r{\frac {\partial u}{\partial y}}{\frac {\partial y}{\partial r}},\\[2pt]{\frac {\partial u}{\partial \theta }}&={\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial \theta }}+{\frac {\partial u}{\partial y}}{\frac {\partial y}{\partial \theta }},\end{aligned}}}
或
r
∂
u
∂
r
=
r
∂
u
∂
x
cos
θ
+
r
∂
u
∂
y
sin
θ
=
x
∂
u
∂
x
+
y
∂
u
∂
y
,
∂
u
∂
θ
=
−
∂
u
∂
x
r
sin
θ
+
∂
u
∂
y
r
cos
θ
=
−
y
∂
u
∂
x
+
x
∂
u
∂
y
.
{\displaystyle {\begin{aligned}r{\frac {\partial u}{\partial r}}&=r{\frac {\partial u}{\partial x}}\cos \theta +r{\frac {\partial u}{\partial y}}\sin \theta =x{\frac {\partial u}{\partial x}}+y{\frac {\partial u}{\partial y}},\\[2pt]{\frac {\partial u}{\partial \theta }}&=-{\frac {\partial u}{\partial x}}r\sin \theta +{\frac {\partial u}{\partial y}}r\cos \theta =-y{\frac {\partial u}{\partial x}}+x{\frac {\partial u}{\partial y}}.\end{aligned}}}
于是,我们可以得到下述关系:
r
∂
∂
r
=
x
∂
∂
x
+
y
∂
∂
y
∂
∂
θ
=
−
y
∂
∂
x
+
x
∂
∂
y
.
{\displaystyle {\begin{aligned}r{\frac {\partial }{\partial r}}&=x{\frac {\partial }{\partial x}}+y{\frac {\partial }{\partial y}}\\[2pt]{\frac {\partial }{\partial \theta }}&=-y{\frac {\partial }{\partial x}}+x{\frac {\partial }{\partial y}}.\end{aligned}}}
利用坐标逆变换,可以得到类似的反向关系。给定一函数u (r ,θ ),我们有
∂
u
∂
x
=
∂
u
∂
r
∂
r
∂
x
+
∂
u
∂
θ
∂
θ
∂
x
,
∂
u
∂
y
=
∂
u
∂
r
∂
r
∂
y
+
∂
u
∂
θ
∂
θ
∂
y
,
{\displaystyle {\begin{aligned}{\frac {\partial u}{\partial x}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial x}}+{\frac {\partial u}{\partial \theta }}{\frac {\partial \theta }{\partial x}},\\[2pt]{\frac {\partial u}{\partial y}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial y}}+{\frac {\partial u}{\partial \theta }}{\frac {\partial \theta }{\partial y}},\end{aligned}}}
或
∂
u
∂
x
=
∂
u
∂
r
x
x
2
+
y
2
−
∂
u
∂
θ
y
x
2
+
y
2
=
cos
θ
∂
u
∂
r
−
1
r
sin
θ
∂
u
∂
θ
,
∂
u
∂
y
=
∂
u
∂
r
y
x
2
+
y
2
+
∂
u
∂
θ
x
x
2
+
y
2
=
sin
θ
∂
u
∂
r
+
1
r
cos
θ
∂
u
∂
θ
.
{\displaystyle {\begin{aligned}{\frac {\partial u}{\partial x}}&={\frac {\partial u}{\partial r}}{\frac {x}{\sqrt {x^{2}+y^{2}}}}-{\frac {\partial u}{\partial \theta }}{\frac {y}{x^{2}+y^{2}}}\\[2pt]&=\cos \theta {\frac {\partial u}{\partial r}}-{\frac {1}{r}}\sin \theta {\frac {\partial u}{\partial \theta }},\\[2pt]{\frac {\partial u}{\partial y}}&={\frac {\partial u}{\partial r}}{\frac {y}{\sqrt {x^{2}+y^{2}}}}+{\frac {\partial u}{\partial \theta }}{\frac {x}{x^{2}+y^{2}}}\\[2pt]&=\sin \theta {\frac {\partial u}{\partial r}}+{\frac {1}{r}}\cos \theta {\frac {\partial u}{\partial \theta }}.\end{aligned}}}
于是,
∂
∂
x
=
cos
θ
∂
∂
r
−
1
r
sin
θ
∂
∂
θ
∂
∂
y
=
sin
θ
∂
∂
r
+
1
r
cos
θ
∂
∂
θ
.
{\displaystyle {\begin{aligned}{\frac {\partial }{\partial x}}&=\cos \theta {\frac {\partial }{\partial r}}-{\frac {1}{r}}\sin \theta {\frac {\partial }{\partial \theta }}\\[2pt]{\frac {\partial }{\partial y}}&=\sin \theta {\frac {\partial }{\partial r}}+{\frac {1}{r}}\cos \theta {\frac {\partial }{\partial \theta }}.\end{aligned}}}
对一条极坐标下曲线r (θ ),要得到其在直角坐标下的切线斜率,先用参数方程 表述该曲线:
x
=
r
(
θ
)
cos
θ
y
=
r
(
θ
)
sin
θ
{\displaystyle {\begin{aligned}x&=r(\theta )\cos \theta \\y&=r(\theta )\sin \theta \end{aligned}}}
把两个等式对 θ 求导 ,得到
d
x
d
θ
=
r
′
(
θ
)
cos
θ
−
r
(
θ
)
sin
θ
d
y
d
θ
=
r
′
(
θ
)
sin
θ
+
r
(
θ
)
cos
θ
.
{\displaystyle {\begin{aligned}{\frac {dx}{d\theta }}&=r'(\theta )\cos \theta -r(\theta )\sin \theta \\[2pt]{\frac {dy}{d\theta }}&=r'(\theta )\sin \theta +r(\theta )\cos \theta .\end{aligned}}}
用第一条等式除第二条,可得曲线在(r (θ ), θ ) 上切线的斜率。
d
y
d
x
=
r
′
(
θ
)
sin
θ
+
r
(
θ
)
cos
θ
r
′
(
θ
)
cos
θ
−
r
(
θ
)
sin
θ
.
{\displaystyle {\frac {dy}{dx}}={\frac {r'(\theta )\sin \theta +r(\theta )\cos \theta }{r'(\theta )\cos \theta -r(\theta )\sin \theta }}.}
向量微积分 也可以应用到极坐标。对于平面运动,令
r
{\displaystyle \mathbf {r} }
(
r
cos
(
θ
)
,
r
sin
(
θ
)
)
{\displaystyle (r\cos(\theta ),r\sin(\theta ))}
r 与随时间t 变化的
θ
{\displaystyle \theta }
r
^
{\displaystyle {\hat {\mathbf {r} }}}
r
{\displaystyle \mathbf {r} }
θ
^
{\displaystyle {\hat {\boldsymbol {\theta }}}}
r
{\displaystyle \mathbf {r} }
d
r
d
t
=
r
˙
r
^
+
r
θ
˙
θ
^
,
{\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},}
d
2
r
d
t
2
=
(
r
¨
−
r
θ
˙
2
)
r
^
+
(
r
θ
¨
+
2
r
˙
θ
˙
)
θ
^
.
{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.}
令
A
{\displaystyle \mathbf {A} }
d
A
{\displaystyle d\mathbf {A} }
r
{\displaystyle \mathbf {r} }
d
r
{\displaystyle d\mathbf {r} }
平行四边形 区域的一半。
d
A
=
1
2
|
r
×
d
r
|
{\displaystyle dA={\begin{matrix}{\frac {1}{2}}\end{matrix}}|\mathbf {r} \times d\mathbf {r} |}
所以,整个区域就是
d
A
{\displaystyle d\mathbf {A} }
极坐标系可被扩展到三维空间中,形成圆柱坐标系 和球坐标系 两个不同的坐标系。
用圆柱坐标
(
ρ
,
φ
,
z
)
{\displaystyle (\rho ,\ \varphi ,\ z)}
与将直角坐标系 扩展为三维的方法相似,圆柱坐标系 是在二维极坐标系的基础上增添了第三条用于测量高于平面的点的高度的坐标所构成的。这第三条坐标通常也表示为z。所以圆柱坐标表示为(ρ, φ, z)。
通过以下公式,可以从直角坐标变换为圆柱坐标:
x
=
ρ
cos
φ
{\displaystyle {x}={\rho }\,\cos \varphi }
y
=
ρ
sin
φ
{\displaystyle {y}={\rho }\,\sin \varphi }
z
=
z
{\displaystyle {z}={z}}
用球坐标
(
r
,
θ
,
φ
)
{\displaystyle (r,\ \theta ,\ \varphi )}
球坐标系 也可以运用坐标(r, θ, φ)扩展为三维,其中r是距离球心的距离,θ是距离z轴的角度(称作余纬度或顶角,角度从0到180°),φ是距离x轴的角度(与极坐标中一样)。这个坐标系被称作球坐标系,与用于地球的经度 和纬度 相似,纬度就是余角θ,取决于δ=90°-θ,经度可通过λ=φ-180°算得。[ 15]
通过以下公式,可以从直角坐标变换为球坐标:
x
=
r
sin
θ
cos
φ
{\displaystyle x=r\,\sin \theta \,\cos \varphi }
y
=
r
sin
θ
sin
φ
{\displaystyle y=r\,\sin \theta \,\sin \varphi }
z
=
r
cos
θ
{\displaystyle z=r\,\cos \theta }
极坐标通常被用于导航 ,作为旅行的目的地或方向可以作为从所考虑的物体的距离和角度。例如,飞机 使用极坐标的一个略加修改的版本进行导航。这个系统中是一般的用于导航任何种类中的一个系统,在0°射线一般被称为航向360,并且角度是以顺时针方向 继续,而不是逆时针方向,如同在数学系统那样。航向360对应地磁北极 ,而航向90,180,和270分别对应于磁东,南,西。[ 16] 海里 将是在航向90(空中交通管制 读作090)上航行5个单位。[ 17]
有径向对称的系统提供了极坐标系的自然设置,中心点充当了极点。这种用法的一个典型例子是在适用于径向对称的水井 时候的地下水流方程 平方反比定律 的引力场 ,以及有点源的系统,如无线电 天线 。
开普勒第二定律 极坐标提供了一个表达在引力场 中开普勒行星运行定律的自然的方法。开普勒第一定律表明,环绕一颗恒星运行的行星轨道形成了一个椭圆 ,这个椭圆的一个焦点在质心 上。上面所给出的二次曲线部分的等式可用于表达这个椭圆。开普勒第二定律表明,连接行星和它所环绕的恒星的线在等时间间隔所划出的区域是面积相等的,即
d
A
d
t
{\displaystyle d\mathbf {A} \over dt}
牛顿运动定律 推得。在开普勒行星运动定律 中有相关运用极坐标的详细推导。
^ The MacTutor History of Mathematics archive: Coolidge's Origin of Polar Coordinates . [2006-10-09 ] . (原始内容存档 于2006-06-01). ^ Coolidge, Julian. The Origin of Polar Coordinates . American Mathematical Monthly. 1952, 59 : 78–85. ^ Klaasen, Daniel. Historical Topics for the Mathematical Classroom. ^ Miller, Jeff. Earliest Known Uses of Some of the Words of Mathematics . [2006-09-10 ] . (原始内容 存档于1999-10-03). ^ Smith, David Eugene. History of Mathematics, Vol II. Boston: Ginn and Co. 1925: 324. ^ Brown, Richard G. Andrew M. Gleason , 编. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis . Evanston, Illinois: McDougal Littell Inc. 1997. ISBN 978-0-395-77114-3 . ^ Polar Coordinates and Graphing (PDF) . [2006-09-22 ] . (原始内容 (PDF) 存档于2012-02-15). ^ Serway, Raymond A. and Jewett, Jr., John W. Principles of Physics. Brooks/Cole—Thomson Learning. 2005. ISBN 978-0-534-49143-7 . ^ Torrence, Bruce Follett; Eve Torrence. The Student's Introduction to Mathematica . Cambridge University Press. 1999. ISBN 0-521-59461-8 ^ Polar coordinates . [2006-05-25 ] . (原始内容 存档于2006-04-27). ^ Ward, Robert L. Analytic Geometry: Polar Coordinates . [2006-05-25 ] . (原始内容存档 于2019-10-09). ^
Smith, Julius O. Euler's Identity . Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. 2003 [2006-09-22 ] . ISBN 978-0-9745607-0-0 . (原始内容 存档于2006-09-15).
^ Husch, Lawrence S. Areas Bounded by Polar Curves . [2006-11-25 ] . (原始内容存档 于2000-03-01). ^ Lawrence S. Husch. Tangent Lines to Polar Graphs . [2006-11-25 ] . (原始内容存档 于2019-11-21). ^ Wattenberg, Frank. Spherical Coordinates . 1997 [2006-09-16 ] . (原始内容 存档于2012-02-15). ^ Santhi, Sumrit. Aircraft Navigation System . [2006-11-26 ] . (原始内容存档 于2019-10-25). ^ Emergency Procedures (PDF) . [2007-01-15 ] . (原始内容存档 (PDF) 于2006-01-03).




















![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)
![{\displaystyle (-180^{\circ },180^{\circ }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52564e11cb8ecd24997d7929ef3ff9a87052b335)

































![{\displaystyle {\begin{aligned}r{\frac {\partial u}{\partial r}}&=r{\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial r}}+r{\frac {\partial u}{\partial y}}{\frac {\partial y}{\partial r}},\\[2pt]{\frac {\partial u}{\partial \theta }}&={\frac {\partial u}{\partial x}}{\frac {\partial x}{\partial \theta }}+{\frac {\partial u}{\partial y}}{\frac {\partial y}{\partial \theta }},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17d13a231f33e10e1702aa67b57e92f0ea46dbdc)
![{\displaystyle {\begin{aligned}r{\frac {\partial u}{\partial r}}&=r{\frac {\partial u}{\partial x}}\cos \theta +r{\frac {\partial u}{\partial y}}\sin \theta =x{\frac {\partial u}{\partial x}}+y{\frac {\partial u}{\partial y}},\\[2pt]{\frac {\partial u}{\partial \theta }}&=-{\frac {\partial u}{\partial x}}r\sin \theta +{\frac {\partial u}{\partial y}}r\cos \theta =-y{\frac {\partial u}{\partial x}}+x{\frac {\partial u}{\partial y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d6955aceb8401ab91fd5376a7f7f039c840a3fc)
![{\displaystyle {\begin{aligned}r{\frac {\partial }{\partial r}}&=x{\frac {\partial }{\partial x}}+y{\frac {\partial }{\partial y}}\\[2pt]{\frac {\partial }{\partial \theta }}&=-y{\frac {\partial }{\partial x}}+x{\frac {\partial }{\partial y}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c15d968d0db9185217ecd72ad43063ec10d351b)
![{\displaystyle {\begin{aligned}{\frac {\partial u}{\partial x}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial x}}+{\frac {\partial u}{\partial \theta }}{\frac {\partial \theta }{\partial x}},\\[2pt]{\frac {\partial u}{\partial y}}&={\frac {\partial u}{\partial r}}{\frac {\partial r}{\partial y}}+{\frac {\partial u}{\partial \theta }}{\frac {\partial \theta }{\partial y}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e708e5dee8ec8f86761efa820abb6040f83ee140)
![{\displaystyle {\begin{aligned}{\frac {\partial u}{\partial x}}&={\frac {\partial u}{\partial r}}{\frac {x}{\sqrt {x^{2}+y^{2}}}}-{\frac {\partial u}{\partial \theta }}{\frac {y}{x^{2}+y^{2}}}\\[2pt]&=\cos \theta {\frac {\partial u}{\partial r}}-{\frac {1}{r}}\sin \theta {\frac {\partial u}{\partial \theta }},\\[2pt]{\frac {\partial u}{\partial y}}&={\frac {\partial u}{\partial r}}{\frac {y}{\sqrt {x^{2}+y^{2}}}}+{\frac {\partial u}{\partial \theta }}{\frac {x}{x^{2}+y^{2}}}\\[2pt]&=\sin \theta {\frac {\partial u}{\partial r}}+{\frac {1}{r}}\cos \theta {\frac {\partial u}{\partial \theta }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d1b608cbc32bda0cfd2267cbf292e8b87b1aac)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial x}}&=\cos \theta {\frac {\partial }{\partial r}}-{\frac {1}{r}}\sin \theta {\frac {\partial }{\partial \theta }}\\[2pt]{\frac {\partial }{\partial y}}&=\sin \theta {\frac {\partial }{\partial r}}+{\frac {1}{r}}\cos \theta {\frac {\partial }{\partial \theta }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2beb1efdc1b8837b2555caeba044a8f17a2fb7f9)

![{\displaystyle {\begin{aligned}{\frac {dx}{d\theta }}&=r'(\theta )\cos \theta -r(\theta )\sin \theta \\[2pt]{\frac {dy}{d\theta }}&=r'(\theta )\sin \theta +r(\theta )\cos \theta .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/745d78e7f022b99221911c170a64c3a5fb39f184)



















