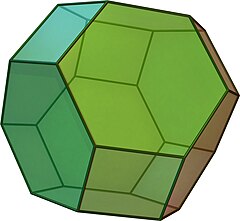
截角八面体
 (按这里观看旋转模型) | |||||
| 类别 | 半正多面体 | ||||
|---|---|---|---|---|---|
| 对偶多面体 | 四角化立方体 | ||||
| 识别 | |||||
| 名称 | 截角八面体 | ||||
| 参考索引 | U08, C20, W7 | ||||
| 鲍尔斯缩写 | toe | ||||
| 数学表示法 | |||||
| 考克斯特符号 | |||||
| 施莱夫利符号 | t0,1{3,4} t0,1,2{3,3} t{3,4} tr{3,3} | ||||
| 威佐夫符号 | 2 4 | 3 3 3 2 | | ||||
| 康威表示法 | tO bT | ||||
| 性质 | |||||
| 面 | 14 | ||||
| 边 | 36 | ||||
| 顶点 | 24 | ||||
| 欧拉特征数 | F=14, E=36, V=24 (χ=2) | ||||
| 组成与布局 | |||||
| 面的种类 | 正方形 正六边形 | ||||
| 面的布局 | 6个{4} 8个{6} | ||||
| 顶点图 | 4.6.6 | ||||
| 对称性 | |||||
| 对称群 | Oh群 and Th | ||||
| 特性 | |||||
| 环带多面体 permutohedron | |||||
| 图像 | |||||
| |||||
在几何学中,截角八面体[1]是一种具有十四个面的半正多面体,属于阿基米德立体也是个平行多面体。由6个正方形和8个正六边形组成,共有14个面、36个边以及24个顶点[2]。因为每个面皆具点对称性质,因此截角八面体也是一种环带多面体。同时,因为它具有正方形和六边形面,因此也是一种戈德堡多面体,其戈德堡符号为GIV(1,1)。另外,由于截角八面体也是一种排列多面体[3][4],因此可以独立填满整个三维空间[5],而由截角八面体堆成的图形称为截角八面体堆砌[6]。
截角八面体的对偶多面体为四角化六面体。若截角八面体的边长为单位长,则其对偶多面体四角化六面体的边长会变成和个单位长。
性质
[编辑]截角八面体仅具有点可递性质,也就是截角八面体每一个顶点相邻面的组成都是一样的,都是一个四边形和两个六边形的公共顶点。但截角八面体不具面可递和边可递性质,因为截角八面体有两种面,四边形和六边形,边也不可递,因为截角八面体并不是所有组成边的相邻面都只有一种,截角八面体共有两种棱,一种为六边形与六边形的公共棱、另一种为六边形与四边形的公共棱。
由于截角八面体仅具有点可递性质,因此只能算是均匀多面体[7]中的半正多面体,不具拟正多面体性质。但这个多面体是阿几米德研究的13种半正多面体之一,因此截角八面体也是一种阿基米德立体[8]。
结构
[编辑]
|
|
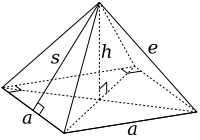
截角八面体可以从边长3a的正八面体切去六个底边长为a的四角锥构成。这些被切下来的棱锥体的底与侧面边长皆等长,因此其侧面皆为正三角形,底边长为a、底面积为a2,这些四角锥是正四角锥,是第一种詹森多面体,J1。
这些被截下来的正四角锥其高h与斜高s为:
这些数据则确定能从正八面体构成截角八面体的截角切割深度。若太深则会变成截半八面体。
坐标
[编辑]
|
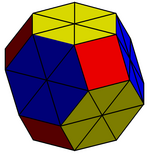
|
| 在(±2,±2,±2)范围内的平行投影 | 每个六边形面切割成六个正三角形产生了八个新的顶点,他们分别为(±1,±1,±1)的所有组合。 |
边长为2的平方根且几何中心位于原点的截角八面体其顶点坐标为(0, ±1, ±2)的所有排列。
体积与表面积
[编辑]截角立方体的体积,表面积,其中是该截半立方体的边长[2]。
- 表面积 = ≈
- 体积 = ≈
作法
[编辑]将正八面体进行截角操作,也就是将正八面体的六个顶点切去并在被切掉的地方建立六个正方形面即可得到一个截角八面体。
正交投影
[编辑]| 建立于 | 顶点 | 边 4-6 |
边 6-6 |
面 正方形 |
面 正六边形 |
|---|---|---|---|---|---|
| 截角八面体 | 
|

|
|

|
|
| 四角化六面体 | 
|
|

|
|

|
| 投影 对称性 |
[2] | [2] | [2] | [4] | [6] |
球面镶嵌
[编辑]
|
 以正方形面为中心 |
 以正六边形面为中心 |
| 平行投影 | 施莱格尔投影 | |
|---|---|---|
分割
[编辑]截角八面体可分割成正中央一个正八面体、其余每个面切成8三角帐塔,剩余的部分在分割成6个正四角锥。[10]
| 亏格 2 | 亏格 3 |
|---|---|
| D3d, [2+,6], (2*3), order 12 | Td, [3,3], (*332), order 24 |

|

|
排列多面体
[编辑]截角八面体是一种排列多面体[3][4],可以以更“对称”的形式表示:四维空间中,(1,2,3,4)所有排列的坐标在三维子空间组成截角八面体。(对应的二维形状是正六边形:三维空间中,(1,2,3)所有排列的坐标在二维子空间组成正六边形。)
相关多面体及镶嵌
[编辑]| 对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|

|

|

|

|

| |||
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| 半正多面体对偶 | |||||||

|

|

|

| ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
| 对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|
||||||
| {4,3} | t0,1{4,3} | t1{4,3} | t1,2{4,3} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | s{4,3} | h{4,3} | h1,2{4,3} |
| 半正多面体的对偶 | |||||||||

|

|

|

|

|

| ||||
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
堆砌
[编辑]
截角八面体可以独立填满整个三维空间,而这种由截角八面体堆砌出来的几何图形称为截角八面体堆砌。
截角八面体堆砌是三维空间内28个半正密铺之一,由截角八面体独立堆积而成,虽然他每个胞都全等、每边皆等长,但其不能称为正密铺,因为虽然她只由一种胞,截角八面体组成,但是该胞不是正多面体,因此并非所有“面”皆全等,因此截角八面体堆砌只能称为半正堆砌。
- 其他堆砌
| 截角八面体堆砌 | 小斜方截半正方体堆砌 | 截角交错立方体堆砌 |
|---|---|---|
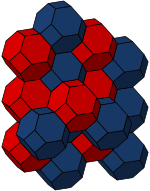
|

|

|
 
|
 
|
 
|
 
|
 
|
 
|
... |
| 过截角立方体 | 过截角超立方体 | 过截角五维超立方体 | 过截角六维超立方体 | 过截角七维超立方体 | 过截角八维超立方体 | |
参见
[编辑]参考文献
[编辑]- ^ Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- ^ 2.0 2.1 Weisstein, Eric W. (编), Truncated Octahedron, (Archimedean solid), at MathWorld--A Wolfram Web Resource,Wolfram Research, Inc. (英语)
- ^ 3.0 3.1 庄宛臻. Type B 的排列多面體. 应用数学系. 高雄大学. 2010-07-03 [2016-01-30]. (原始内容存档于2016-01-30).
- ^ 4.0 4.1 Cayley graph of S4. This Cayley graph labeling is shown, e.g., by Ziegler (1995).
- ^ Freitas, Robert A., Jr. Uniform space-filling using only truncated octahedra. Figure 5.5 of Nanomedicine, Volume I: Basic Capabilities, Landes Bioscience, Georgetown, TX, 1999. [2006-09-08]. (原始内容存档于2006-01-14). 外部链接存在于
|publisher=(帮助) - ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- ^ Mäder, Roman. The Uniform Polyhedra: Truncated Octahedron. [2006-09-08]. (原始内容存档于2006-09-11).
- ^ Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
- ^ Hart, George W. VRML model of truncated octahedron. Virtual Polyhedra: The Encyclopedia of Polyhedra. [2006-09-08]. (原始内容存档于2006-08-22). 外部链接存在于
|publisher=(帮助) - ^ Alex Doskey. Chapter 5 - Simplest (R)(A)(Q)(T) Toroids of genus p=1. Alexander's Polyhedra. doskey.com. 2006 [2016-01-30]. (原始内容存档于2016-02-04).
- Gaiha, P., and Guha, S.K. Adjacent vertices on a permutohedron. SIAM Journal on Applied Mathematics. 1977, 32 (2): 323–327. doi:10.1137/0132025.
- Alexandrov, A.D. Convex polyhedra. Berlin: Springer. 1958: 539. ISBN 3-540-23158-7.
- Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
外部链接
[编辑]- 埃里克·韦斯坦因, 截角八面体 (参阅阿基米德立体) 于MathWorld(英文)
- 埃里克·韦斯坦因. Permutohedron. MathWorld.
- Klitzing, Richard. 3D convex uniform polyhedra x3x4o - toe. bendwavy.org.
- Editable printable net of a truncated octahedron with interactive 3D view (页面存档备份,存于互联网档案馆)
- 截角八面体形状的扭计骰:Fisher's Truncated Octahedron (页面存档备份,存于互联网档案馆)、Truncated Octaminx (页面存档备份,存于互联网档案馆)












































