多重对数函数
外观
此条目需要精通或熟悉相关主题的编者参与及协助编辑。 (2011年1月8日) |
多重对数函数(英语:polylogarithm,也称:Jonquière's function)是数学中一种特殊的幂级数,定义为:
一般来说,多重对数函数不像对数函数那样是一个初等函数。上述定义中,自变量|z| < 1,s对所有复数值有效。通过解析延拓,可以将z的定义域扩展到更大的范围。
 |
 |
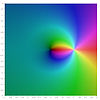 |
 |
 |
 |
 |
s = 1时的多重对数函数可以用自然对数表示(Li1(z) = −ln(1−z)),s = 2和3的多重对数函数分别称为dilogarithm及trilogarithm,其名称的由来是多重对数函数表示为以下的递回积分式:
因此s = 2的多重对数函数可表示为自然对数的积分,以此类推。若其阶数s为零或负的整数,其多重对数函数为有理函数。
多重对数函数出现在费米-狄拉克分布及玻色-爱因斯坦分布解析解的积分式中,因此也称为费米-狄拉克积分或玻色-爱因斯坦积分。
外部链接
[编辑]- 埃里克·韦斯坦因. Polylogarithm. MathWorld.
- 埃里克·韦斯坦因. Dilogarithm. MathWorld.
- Algorithms in Analytic Number Theory (页面存档备份,存于互联网档案馆) provides an arbitrary-precision, GNU多重精度运算库-based, GPL-licensed implementation.









