点积

本文介绍向量的标量积。关于其他常称作内积的相关二元运算，参见内积。

在数学中，点积（德語：Punktprodukt；英語：dot product）又称数量积或标量积（德語：Skalarprodukt；英語：scalar product），是一种接受两串等长的数字序列（通常是坐标向量）、返回单一数字的代数运算。

在欧几里得几何里，两條笛卡尔坐标向量的点积常称为内积（德語：inneres Produkt；英語：inner product）。點积是内积的一种特殊形式：内积是点积的抽象，內积是一种双线性函数，点积是欧几里得空间（内积空间）的度量。

从代数角度看，先求两数字序列中每组对应元素的积，再求所有积之和，结果即为点积。从几何角度看，点积则是两向量的长度与它们夹角余弦的积。这两种定义在笛卡尔坐标系中等价。

点积的名称源自表示点乘运算的点号（$\mathbf {a} \cdot \mathbf {b}$），讀作a dot b，标量积的叫法则是在强调其运算结果为标量而非向量。向量的另一种乘法是叉乘（$\mathbf {a} \times \mathbf {b}$），讀作a cross b，其结果为向量，称为叉积或向量积。

定义

点积有两种定义方式：代数方式和几何方式。通过在欧氏空间中引入笛卡尔坐标系，向量间的点积既可以由向量坐标的代数运算得出，也可以通过引入两向量的长度和角度等几何概念来求解。

代数定义

向量${\vec {a}}=[a_{1},a_{2},\cdots ,a_{n}]$和${\vec {b}}=[b_{1},b_{2},\cdots ,b_{n}]$的点积定义为：

${\vec {a}}\cdot {\vec {b}}=\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

这裡的Σ是求和符号，而n是向量空間的維度。

例如，三维向量$\left[1,3,-5\right]$和$\left[4,-2,-1\right]$的点积是

${\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1)(4)+(3)(-2)+(-5)(-1)\\&=4-6+5\\&=3\end{aligned}}$

点积还可以写为：

${\vec {a}}\cdot {\vec {b}}={\vec {a}}{\vec {b}}^{T}$。

这裡，${\vec {b}}^{T}$是列向量${\vec {b}}$的转置。

使用上面的例子，1×3矩阵（列向量）乘以3×1矩阵（行向量）的行列式就是结果(通过矩阵乘法得到1×1矩陣):

${\begin{bmatrix}1&3&-5\end{bmatrix}}{\begin{bmatrix}4\\-2\\-1\end{bmatrix}}={\begin{bmatrix}3\end{bmatrix}}=3$。

几何定义

在欧几里得空间中，点积可直观定义为

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\cos \theta \;$

这里 |${\vec {x}}$| 表示${\vec {x}}$的模（长度），$\theta$表示向量间的角度。

注意：点积的形式定义和这定义不同；在形式定义，${\vec {a}}$和${\vec {b}}$的夹角用上述等式定义。

这样，互相垂直的两條向量的点积总是零。若${\vec {a}}$和${\vec {b}}$都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两條向量，它们之间的夹角可以以下公式得到：

$\cos {\theta }={\frac {\mathbf {a\cdot b} }{|{\vec {a}}|\,|{\vec {b}}|}}$

这个运算可以简单地理解为：在点积运算中，第一向量投影到第二向量上（向量顺序这裡在不重要，点积运算可交换），然后通过除以它们的标量长度来“标准化”。这样，这分数一定是小于等于1的，可以简单转化成角度值。

标量投影

$\mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos(\theta )$。
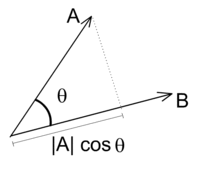
$|\mathbf {A} |\cos(\theta )$是$\mathbf {A}$到$\mathbf {B}$的投影。

欧氏空间中向量$\mathbf {A}$在向量$\mathbf {B}$上的标量投影是指對於向量B來說向量A的垂直度到向量B的代表長度

$A_{B}=|\mathbf {A} |\cos \theta$

这里$\theta$是$\mathbf {A}$和$\mathbf {B}$的夹角。从点积的几何定义$\mathbf {A} \cdot \mathbf {B} =|\mathbf {A} ||\mathbf {B} |\cos \theta$不难得出，两向量的点积：$\mathbf {A} \cdot \mathbf {B}$可以理解为向量$\mathbf {A}$在向量$\mathbf {B}$上的投影再乘以$\mathbf {B}$的长度。

$\mathbf {A} \cdot \mathbf {B} =A_{B}|\mathbf {B} |=B_{A}|\mathbf {A} |$

两种定义的等价性

点积的两种定义中，只需给定一种定义，另外一种定义就可以推出。

由几何定义推出代数定义

设$e_{1},...,e_{n}$是$\mathbb {R} ^{n}$空间的一组标准正交基，可以得出：

${\begin{aligned}\mathbf {A} &=[a_{1},\dots ,a_{n}]=\sum _{i}a_{i}\mathbf {e} _{i}\\\mathbf {B} &=[b_{1},\dots ,b_{n}]=\sum _{i}b_{i}\mathbf {e} _{i}.\end{aligned}}$

上文中已经得知两條向量点积的几何定义实际上就是一條向量在另外一條向量上的投影，故$\mathbf {A}$在任一标准基$e_{n}$的点积$\mathbf {A} \cdot \mathbf {e} _{i}$就是$\mathbf {A}$在此标准基向量上的投影，而根据向量自身的定义，这个投影即为$a_{i}$。因此：

$\mathbf {A} \cdot \mathbf {B} =\mathbf {A} \cdot \sum _{i}b_{i}\mathbf {e} _{i}=\sum _{i}b_{i}(\mathbf {A} \cdot \mathbf {e} _{i})=\sum _{i}b_{i}a_{i}$

由代数定义推出几何定义

应用余弦定理。 注意：这个证明采用三维向量，但可以推广到$n$维的情形。

考虑向量

${\vec {v}}=v_{1}{\vec {i}}+v_{2}{\vec {j}}+v_{3}{\vec {k}}\;$.

重復使用勾股定理得到

$|{\vec {v}}|^{2}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}\;$.

而由代数定义

${\vec {v}}\cdot {\vec {v}}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}\;$,

所以，根据向量点积的代数定义，向量${\vec {v}}$和自身的点积就是其长度的平方。

引理1

${\vec {v}}\cdot {\vec {v}}=|{\vec {v}}|^{2}\;$

现在，考虑从原点出发的两條向量${\vec {a}}$和${\vec {b}}$，夹角$\theta$。第三條向量${\vec {c}}$定义为

${\vec {c}}\equiv {\vec {a}}-{\vec {b}}\;$,

构造以${\vec {a}}$，${\vec {b}}$，${\vec {c}}$为边的三角形，采用余弦定理，有

$|{\vec {c}}|^{2}=|{\vec {a}}|^{2}+|{\vec {b}}|^{2}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$.

根据引理1，用点积代替向量长度的平方，有

${\vec {c}}\cdot {\vec {c}}={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$. （1）

同时，根据定义${\vec {c}}$ ≡ ${\vec {a}}$ - ${\vec {b}}$，有

${\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})\;$,

根据分配律，得

${\vec {c}}\cdot {\vec {c}}={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2({\vec {a}}\cdot {\vec {b}})\;$. （2）

连接等式（1）和（2）有

${\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2({\vec {a}}\cdot {\vec {b}})={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2|{\vec {a}}||{\vec {b}}|\cos \theta \;$.

简化等式即得

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}||{\vec {b}}|\cos \theta \;$,

以上即为向量点积的几何定义。

需要注意的是，点积的几何解释通常只适用于$\mathbb {R} ^{n}$ ($n\leq 3$)。在高维空间，其他的域或模中，点积只有一个定义，那就是

$\left\langle {\vec {a}},{\vec {b}}\right\rangle =\sum _{i=1}^{n}a_{i}b_{i}$

点积可以用来计算合力和功。若${\vec {b}}$为单向量，则点积即为${\vec {a}}$在方向${\vec {b}}$的投影，即给出了力在这个方向上的分解。功即是力和位移的点积。

性质

点积有以下性质。

• 满足交换律：

  ${\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}$，

  从定义即可证明（$\theta$ 为$a$与$b$的夹角）：

  ${\vec {a}}\cdot {\vec {b}}=\left\|{\vec {a}}\right\|\left\|{\vec {b}}\right\|\cos \theta =\left\|{\vec {b}}\right\|\left\|{\vec {a}}\right\|\cos \theta ={\vec {b}}\cdot {\vec {a}}$

• 对向量加法满足分配律：

  ${\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}$

• 点积是双线性算子：

  ${\vec {a}}\cdot (r{\vec {b}}+{\vec {c}})=r({\vec {a}}\cdot {\vec {b}})+({\vec {a}}\cdot {\vec {c}})$

• 在乘以标量时满足：

  $(c_{1}{\vec {a}})\cdot (c_{2}{\vec {b}})=(c_{1}c_{2})({\vec {a}}\cdot {\vec {b}})$

• 不满足结合律。因为标量（${\vec {a}}\cdot {\vec {b}}$）与向量（${\vec {c}}$）的点积没有定义，所以结合律相关的表达式 $({\vec {a}}\cdot {\vec {b}})\cdot {\vec {c}}$ 和 ${\vec {a}}\cdot ({\vec {b}}\cdot {\vec {c}})$ 都没有良好的定义

• 两个非零向量${\vec {a}}$和${\vec {b}}$是正交的，当且仅当${\vec {a}}\cdot {\vec {b}}=0$

如果${\vec {b}}$是单位向量，则点积给出${\vec {a}}$在方向${\vec {b}}$上投影的大小，如果方向相反则带有负号。分解向量对求向量的和经常是有用的，比如在力学中计算合力。

不像普通数的乘法服从消去律，如果$ab=ac$，则$b$总是等于$c$，除非$a$等于零。而对于点积：

如果${\vec {a}}\cdot {\vec {b}}={\vec {a}}\cdot {\vec {c}}$并且${\vec {a}}\neq 0$:

则根据分配律可以得出：${\vec {a}}\cdot \left({\vec {b}}-{\vec {c}}\right)=0$；进而：

如果${\vec {a}}$垂直于$\left({\vec {b}}-{\vec {c}}\right)$，则$\left({\vec {b}}-{\vec {c}}\right)$可能$\neq 0$，因而${\vec {b}}$可能$\neq {\vec {c}}$；否则${\vec {b}}={\vec {c}}$。

延伸

矩阵

矩阵具有弗罗比尼乌斯内积，可以类比于向量的内积。它被定义为两个相同大小的矩阵A和B的对应元素的内积之和。

复矩阵情况下：

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\mathrm {tr} (\mathbf {B} ^{\mathrm {H} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {H} }).$

实矩阵情况下：

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\mathrm {tr} (\mathbf {B} ^{\mathrm {T} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {T} })=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} }\mathbf {B} )=\mathrm {tr} (\mathbf {B} \mathbf {A} ^{\mathrm {T} }).$

应用

物理学中力学的力做功的问题，经常用到点积计算。

计算机图形学常用来判断方向，如两向量点积大于0，则它们的方向朝向相近；如果小于0，则方向相反。

向量内积是人工智能领域中的神经网络技术的数学基础之一。

此方法用于动画渲染（Animation-Rendering）。

广义定义

在向量空间$V$中，定義在$V\times V$上的正定对称双线性形式函數即是$V$的內積，而添加有数量积的向量空间即是内积空间。

参见

• 向量积