| 反正割 |
 |
| 性質 |
| 奇偶性 | 非奇非偶 |
| 定義域 |  [1] [1] |
| 到達域 | 
 |
| 周期 | N/A |
| 特定值 |
| 當x=0 | 不存在[註 1] |
| 當x=+∞ | 
(90°) |
| 當x=-∞ | 
(90°) |
| 當x=1 | 0 |
| 當x=-1 | 
(180°) |
| 其他性質 |
| 渐近线 | 
(y=90°) |
反正割(英語:arcsecant[3]、記為: 或
或 )是一種反三角函數[4],對應的三角函數為正割函數,用來計算已知斜邊與鄰邊的比值求出其夾角大小的函數,是高等數學中的一種基本特殊函數,其輸入值與反餘弦互為倒數。
)是一種反三角函數[4],對應的三角函數為正割函數,用來計算已知斜邊與鄰邊的比值求出其夾角大小的函數,是高等數學中的一種基本特殊函數,其輸入值與反餘弦互為倒數。
由於正割函數在實數上不具有一一對應的關係,所以不存在反函數,但我們可以限制其定義域,因此,反正割是單射也是可逆的,由於限制正割函數的定義域在![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751) ([0, 180°])时,其值域是全體實數,但在區間
([0, 180°])时,其值域是全體實數,但在區間![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) 不存在。
不存在。
反正割一般記為 [5]或
[5]或 [6][7][8][9],以表示正割的反函數。也有以大寫書寫的版本Arcsec z[10]和Sec-1 z一般用於表示多值函數[6]。在符號
[6][7][8][9],以表示正割的反函數。也有以大寫書寫的版本Arcsec z[10]和Sec-1 z一般用於表示多值函數[6]。在符號 上的上標-1是表示反函數,而不是乘法逆元素。但根據ISO 31-11應將反正切函數記為
上的上標-1是表示反函數,而不是乘法逆元素。但根據ISO 31-11應將反正切函數記為 ,因為
,因為 可能會與
可能會與 混淆,
混淆, 是餘弦函數。
是餘弦函數。
原始的定義是將正割函數限制在![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751) ([0, 180°])的反函數
([0, 180°])的反函數
在複變分析中,反正割是這樣定義的:

這個動作使反正割被推廣到複數。
下圖表示推廣到複數的反正割複數平面函數圖形,可以見到圖中央有一條明顯的橫線正好是實數中未被定義的區間[-1,1]。
 拓展到複數的反正割函數
拓展到複數的反正割函數
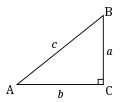
在直角三角形中,反正割定義為已知斜邊c與鄰邊b比值對應的 的大小,也就是:
的大小,也就是:

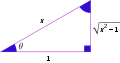
此外在直角三角形中,若已知斜邊為 且鄰邊為單位長,
且鄰邊為單位長, 代入反正割可求得對應的角的大小:
代入反正割可求得對應的角的大小:

因此,根據畢氏定理可以使反正割利用其他反三角函數表示:



若 是平面直角坐标系xOy中的一個未知的象限角,
是平面直角坐标系xOy中的一個未知的象限角, 是角的终边上一点,
是角的终边上一点, 是P到原点O的距离,若已知
是P到原点O的距离,若已知 ,則可利用反正割求得未知的象限角
,則可利用反正割求得未知的象限角 :
:

反正割函數可以使用無窮級數定義:
![{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left({\frac {1}{z}}\right)\\&{}={\frac {\pi }{2}}-[z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots ]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64761e73f4238c32bdd180b393f18cfc458298fa)
反正割函數的泰勒展開式為:

- ^ 由於反正割在x=0未定義,因此考慮複變反正割函數,[2]但由在x=0時於左極限不等於右極限,因此也不存在極限因此Arcsec 0不存在。
- ^ Weisstein, Eric W. "Inverse Secant." From MathWorld--A Wolfram Web Resource.
- ^ 反正割在x=0的極限 wolframalpha.com [2014-08-08]
- ^ 反正割arcsecant-學術名詞資訊 (页面存档备份,存于互联网档案馆) 國家教育研究院 terms.naer.edu.tw [2014-08-07]
- ^ Gradshtein, I. S., I. M. Ryzhik, et al. (2000). Table of integrals, series, and products, Academic Pr.
- ^ Zwillinger, D.(Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.
- ^ 6.0 6.1 Abramowitz, M. and Stegun, I. A.(Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing (页面存档备份,存于互联网档案馆). New York: Dover, pp. 79-83, 1972.
- ^ Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science (页面存档备份,存于互联网档案馆). New York: Springer-Verlag, p. 315, 1998.
- ^ Jeffrey, A. Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, 2000.
- ^ 《 Exponentielle & logarithme 》, § Fonctions circulaires réciproques, Dictionnaire de mathématiques – algèbre, analyse, géométrie, Encyclopædia Universalis.
- ^ Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 141-143, 1987.











![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
















![{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left({\frac {1}{z}}\right)\\&{}={\frac {\pi }{2}}-[z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots ]\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left[{\frac {(2n)!}{2^{2n}(n!)^{2}}}\right]{\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64761e73f4238c32bdd180b393f18cfc458298fa)

