反餘弦(arccosine,  ,
,  )是一種反三角函數,也是高等數學中的一種基本特殊函數。在三角學中,反餘弦被定義為一個角度,也就是餘弦值的反函數,然而餘弦函數是雙射且不可逆的而不是一個對射函數(即多個值可能只得到一個值,例如1和所有同界角),故無法有反函數,但我們可以限制其定義域,因此,反餘弦是單射和滿射也是可逆的,另外,我們也需要限制值域,且限制值域時,不能和反正弦定義相同的區間,因為這樣會變成一對多,而不構成函數,所以我們將反餘弦函數的值域定義在
)是一種反三角函數,也是高等數學中的一種基本特殊函數。在三角學中,反餘弦被定義為一個角度,也就是餘弦值的反函數,然而餘弦函數是雙射且不可逆的而不是一個對射函數(即多個值可能只得到一個值,例如1和所有同界角),故無法有反函數,但我們可以限制其定義域,因此,反餘弦是單射和滿射也是可逆的,另外,我們也需要限制值域,且限制值域時,不能和反正弦定義相同的區間,因為這樣會變成一對多,而不構成函數,所以我們將反餘弦函數的值域定義在![{\displaystyle \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8e34615383b8ffe6f079cfd094c2b274fab51a4) ([0,180°])。另外,在原始的定義中,若輸入值不在區間
([0,180°])。另外,在原始的定義中,若輸入值不在區間![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) ,是沒有意義的,但是三角函數擴充到複數之後,若輸入值不在區間
,是沒有意義的,但是三角函數擴充到複數之後,若輸入值不在區間![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) ,將傳回複數。
,將傳回複數。
反餘弦的數學符號是 ,最常被記為
,最常被記為 。在不同的編程語言和有些計算器則使用acos或acs。
。在不同的編程語言和有些計算器則使用acos或acs。
原始的定義是將餘弦函數限制在![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751) ([0,180°])的反函數
([0,180°])的反函數
在複變分析中,反餘弦是這樣定義的:

這個動作使反餘弦被推廣到複數。
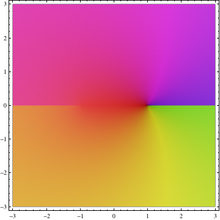 拓展到複數的反餘弦函數
拓展到複數的反餘弦函數
反餘弦函數是一個定義在區間![{\displaystyle \left[-1,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad) 的嚴格遞減連續函數。
的嚴格遞減連續函數。
![{\displaystyle \arccos :\left[-1,1\right]\rightarrow \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9dd622c97420ff8a1cdbdc5b790802c4e6700b1)
- (
![{\displaystyle \arccos :\left[-1,1\right]\rightarrow \left[0,180^{\circ }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89d9e6e44f345333622d37f4fd5dd06cb65e1e64) )
)
其圖形是對稱的,即對稱於點 ,或表示為
,或表示為 ,所以滿足
,所以滿足
反餘弦函數的導數是:
 .
.
反餘弦函數的泰勒級數是:

基於上述級數在 接近1時收斂速度十分緩慢,在
接近1時收斂速度十分緩慢,在 求得的泰勒級數是:
求得的泰勒級數是:

由於先前描述的對稱關係 ,可由上式計算
,可由上式計算 接近1時的反餘弦值。
接近1時的反餘弦值。
也可以用反餘弦和差公式將兩個餘弦值合併成一個餘弦值:

 .
.
直角三角形的輻角為其鄰邊和斜邊之間的比率的反餘弦值。



![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)







![{\displaystyle \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8e34615383b8ffe6f079cfd094c2b274fab51a4)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle \left[-1,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad)
![{\displaystyle \arccos :\left[-1,1\right]\rightarrow \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9dd622c97420ff8a1cdbdc5b790802c4e6700b1)
![{\displaystyle \arccos :\left[-1,1\right]\rightarrow \left[0,180^{\circ }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89d9e6e44f345333622d37f4fd5dd06cb65e1e64)










