跳转到内容
连带勒让德函数是连带勒让德多项式的推广。
下列连带勒让德方程的解,称为连带勒让德函数
![{\displaystyle (1-x^{2})\,y''-2xy'+\left[\lambda (\lambda +1)-{\frac {\mu ^{2}}{1-x^{2}}}\right]\,y=0,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd12eaa0c0059a54a91bc1f6a0e193da811969db)
![{\displaystyle P_{\lambda }^{\mu }(z)={\frac {1}{\Gamma (1-\mu )}}\left[{\frac {1+z}{1-z}}\right]^{\mu /2}\,_{2}F_{1}(-\lambda ,\lambda +1;1-\mu ;{\frac {1-z}{2}}),\qquad {\text{for }}\ |1-z|<2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8005da9a18b4d6bf5cc92e77da81fa9f8a27f88f)
 Associated Legendre P function
Associated Legendre P function
 Associated Legendre P function
Associated Legendre P function

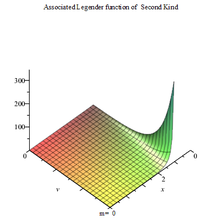 Associated Legendre Q function
Associated Legendre Q function
 Associated Legendre Q function
Associated Legendre Q function
 Associated Legendre Q function
Associated Legendre Q function
 Associated Legendre Q function
Associated Legendre Q function
 Associated Legendre Q function
Associated Legendre Q function
- Courant, Richard; Hilbert, David, Methods of Mathematical Physics, Volume 1, New York: Interscience Publisher, Inc, 1953 .
- Dunster, T. M., Legendre and Related Functions, Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (编), NIST Handbook of Mathematical Functions, Cambridge University Press, 2010, ISBN 978-0521192255, MR2723248
- Ivanov, A.B., L/l058030, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
- Snow, Chester, Hypergeometric and Legendre functions with applications to integral equations of potential theory, National Bureau of Standards Applied Mathematics Series, No. 19, Washington, D.C.: U. S. Government Printing Office, 1952 [1942], MR 0048145
- Whittaker, E. T.; Watson, G. N., A Course in Modern Analysis, Cambridge University Press, 1963, ISBN 978-0-521-58807-2








![{\displaystyle (1-x^{2})\,y''-2xy'+\left[\lambda (\lambda +1)-{\frac {\mu ^{2}}{1-x^{2}}}\right]\,y=0,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd12eaa0c0059a54a91bc1f6a0e193da811969db)
![{\displaystyle P_{\lambda }^{\mu }(z)={\frac {1}{\Gamma (1-\mu )}}\left[{\frac {1+z}{1-z}}\right]^{\mu /2}\,_{2}F_{1}(-\lambda ,\lambda +1;1-\mu ;{\frac {1-z}{2}}),\qquad {\text{for }}\ |1-z|<2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8005da9a18b4d6bf5cc92e77da81fa9f8a27f88f)
