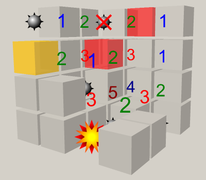
踩地雷
| 「扫雷」的各地常用名稱 | |
|---|---|
| 中国大陸 | 扫雷 |
| 臺灣 | 踩地雷 |
扫雷（英語：Minesweeper）是一类逻辑谜题类电子游戏，通常在个人电脑上游玩。游戏界面由一系列可点击的方块组成，某些方块中隐藏着「地雷」。玩家的目标是尽可能打开所有无雷方块，但不能触发地雷。已打开方块上显示的数字展现了周围地雷数量。
在基本玩法之上，还衍生出了许多其他版本，例如《Minesweeper X》、《Crossmines》、《Minehunt》等。此外，扫雷也被嵌入到其他游戏中作为小游戏出现，如《RuneScape》，以及《我的世界》2015年愚人节更新后的版本。
至于扫雷的起源，目前仍不十分明确。TechRadar认为最早的版本是1990年的《微软扫雷》；但Eurogamer则称，1983年由伊恩·安德鲁开发的《Mined-Out》才是首款扫雷游戏。《微软扫雷》的开发者柯特·约翰逊（Curt Johnson）承认，他在设计游戏时借鉴了其他游戏，但并不是《Mined-Out》。
玩法
[编辑]扫雷为益智游戏。[1]游戏中，地雷随机散布在由许多方块构成的区域内。每个方块有三种状态：未打开、已打开、已标记。未打开的方块为空白且可供点击；一旦点击打开，方块便会显示相应信息；而标记则是玩家用来标示可能藏有地雷的位置。[2]
玩家点击任一方块将其打开：如果点到了地雷，游戏就结束；反之，方块会显示一个数字，代表其周围（包括对角线方向）隐藏的地雷数量，或者显示为空白（也可视作「0」）。当显示为空白时，与其相邻且没有地雷的方块会自动一并打开。[2]玩家也可以手动标记方块（通常会显示一个小旗），以提示该处可能有地雷。[1]被标记的方块仍被视作未打开，玩家随时可以点击它们。[2]在部分版本中，如果某个已打开方块周围显示的数字等于周边已标记方块的数量，则会自动打开所有未标记的相邻方块，这个操作称为「chording」。[2]
目标与策略
[编辑]一局扫雷游戏开始于玩家首次点击某个方块。在某些版本中，首次点击总是安全的，有的甚至保证第一次点击后，该方块周围的所有方块都没有地雷。[3]游戏过程中，玩家需要依靠已打开方块显示的信息，逐步推断出哪些方块没有地雷，并继续打开它们。同时，游戏中会显示剩余地雷的数量，该数值等于地雷总数减去已标记的方块数。因此，若标记过多，地雷数量可能会为负数。[4]
要顺利通关，玩家必须在不触发任何地雷的情况下，将所有无雷方块打开。游戏没有得分，但会记录玩家完成游戏所用的时间。难度可以通过增加地雷数量或使用更大的区域来提升。对于那些没有固定区域的版本，通常会提供三种默认设置：初级、中级、高级，难度依次递增。一般来说，初级多为8×8或9×9的区域，包含10个地雷；中级为16×16，含40个地雷；高级则为30×16，含99个地雷。不过，大部分版本都允许玩家自定义区域尺寸和地雷数量。[2]
- 一局初级（9×9）难度的扫雷游戏从开始到完成的过程
-
-
-
-
-
-
-
-
-
历史
[编辑]根据TechRadar的说法，扫雷是微软在1990年代开发的；[5]但Eurogamer称，伊恩·安德鲁于1983年为ZX Spectrum开发了游戏《Mined-Out》，该游戏「较不为人知、设计精巧」，其他扫雷游戏深受其启发；[6]安德鲁本人更称，《微软扫雷》抄袭了《Mined-Out》。[6]《微软扫雷》首次出现在1990年随Windows 3.11附送的微软娱乐包中，[6][1]由罗伯特·唐纳（Robert Donner）和柯特·约翰逊（Curt Johnson）开发。[5][6]约翰逊曾表示，《微软扫雷》的设计借鉴了另一款游戏，不过并非《Mined-Out》，他自称忘记具体是哪款游戏了。[6]2001年，意大利「国际禁扫雷运动」（International Campaign to Ban Winmine）认为游戏「冒犯了地雷受难者」，[7]要求更换游戏题材。[5]随后，Windows Vista版的《微软扫雷》在设计上做了调整，用鲜花代替了原本的地雷图块。[5][1]
另一早期版本是SunOS上的游戏《Mines》，由汤姆·安德森（Tom Anderson）编写，于1987年发布；据minesweeper.com介绍，该游戏于1990年被移植到X窗口系统上。[8]
游戏常被捆绑在操作系统和桌面环境中，包括IBM的OS/2、Microsoft Windows、KDE、GNOME、Palm OS。[9]2012年Windows 8推出前，微软扫雷一直是Windows的预装游戏。[10]此后，微软推出了一款免费试玩版扫雷，可从Microsoft Store下载，但据How-To Geek介绍，该版本「广告满天飞」。[10][1]
其他版本
[编辑]在传统扫雷的基础上，出现了许多扩展玩法，增添了不少新元素。《Minesweeper X》是《微软扫雷》的仿品，改进了随机性和统计功能，[6][1]因此很受那些追求极速通关的玩家欢迎。[6]《Arbiter》和《Viennasweeper》也是类似的仿品，功能上与《Minesweeper X》类似。[6]《Crossmines》增加了连锁地雷和不规则区块，使玩法更复杂。[5]《BeTrapped》则将扫雷的设定转化为解谜游戏。[5]此外，网上还有不少直接模仿《微软扫雷》的版本。[1]
扫雷还以不同形式出现在其他游戏中：《RuneScape》中的小游戏Vinesweeper借鉴了扫雷；[6]非日文版的《宝可梦 心金/魂银》包含了扫雷的变体；[11]2015年《我的世界》在愚人节更新中添加了扫雷小游戏；[12]HP-48G图形计算器内置的「Minehunt」要求玩家从游戏区域的一角安全移动到另一角，提示仅为周围地雷数；[13]在Google搜索中搜索「扫雷」后，就能触发隐藏的扫雷彩蛋。[14]
另外，还有一种适合纸上玩的逻辑益智版扫雷：开始时部分方块已经显示，玩家无法再打开更多方块，只能正确标记剩余的地雷。与传统扫雷不同，这类谜题通常只有唯一解。2008—2009年间，这类谜题以「天体图」的名义，出现在西南航空的杂志《Spirit》上。[15]
-
天体图谜题 -
非矩形版 -
3D版 -
六边形版 -
三角形版 -
单格多雷版 -
表情符号版
竞技
[编辑]竞技扫雷的玩家目标是在最短时间内通关，他们往往会记住各种常见的数字组合来缩短解题时间。[1]有的玩家会用一种叫做“1.5点击”的技巧，帮助更快地揭示周围的地雷，而也有玩家选择不标记地雷。[1]目前，形成了专门的扫雷玩家社区，相关讨论主要集中在Minesweeper.info等网站上。[6]据《吉尼斯世界纪录大全》记载，截至2025年，最快完成扫雷三种难度记录的是Kamil Murański于2014年创造的38.65秒。[1][16]
计算复杂性
[编辑]2000年，萨迪·凯（Sadie Kaye）[17]提出证明：在扫雷游戏中，给定一个由已揭示（显示数字）、已正确标记和未知状态的方格组成的雷区（且所有已揭示方格的数字均已显示），判断是否存在一种地雷布置，使得该局面符合游戏规则，这一问题是NP完全的。她使用构造性证明，即提供了一种方法，可以将任意布尔电路快速转化为这样一个雷区；而且，该雷区存在合法的地雷布局，当且仅当原布尔电路可满足。利用这种地雷布局作为证明证据，就证明了该问题属于NP类。[18]
不过，如果一个扫雷局面已经保证自洽（数字、标记和未知方格之间没有矛盾），那么判断其是否有解的问题目前虽未被证明为NP完全，但已被证明为co-NP完全。[19]在这种情况下，扫雷还表现出类似于k-SAT的相变现象：当雷区中超过25%的方格含有地雷时，要解出局面就只能依赖猜测，而猜对正确地雷布局的概率非常低，并且随着局面规模增大，这个概率会呈现指数级下降。[20]
参考
[编辑]脚注
[编辑]- ^ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 Edwards, Benj. 30 Years of 'Minesweeper' (Sudoku with Explosions). How-To Geek. 2020-10-08 [2022-08-02] （英语）.
- ^ 2.0 2.1 2.2 2.3 2.4 How To Play Minesweeper. Authoritative Minesweeper. [2022-04-22]. （原始内容存档于2022-06-12） （英语）.
- ^ Minesweeper Strategy - First Click. Authoritative Minesweeper. [2022-04-02]. （原始内容存档于2022-04-02） （英语）.
Windows Vista introduced guaranteed openings [a cell with no adjacent mines] on the first click...
- ^ Leonhard, Woody. Windows 7 All-in-One For Dummies. John Wiley & Sons. 2009-08-19. ISBN 9780470550168 –通过Google Books （英语）.
- ^ 5.0 5.1 5.2 5.3 5.4 5.5 Cobbett, Richard. The most successful game ever: a history of Minesweeper. TechRadar. 2009-05-05 [2022-02-13]. （原始内容存档于2022-02-13） （英语）.
- ^ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 Griliopoulos, Dan. Every step you take: The story of Minesweeper. Eurogamer. 2014-07-20 [2022-07-24]. （原始内容存档于2022-07-20） （英国英语）.
- ^ Blincoe, Robert. Windows Minesweeper is an 'offence to mine victims'. The Register. [2022-07-24]. （原始内容存档于2022-07-24） （英国英语）.
- ^ Minesweeper Game Downloads. minesweepergame.com. [2024-12-14] （英语）.
- ^ Minesweeper (Game): 25 Fun / Interesting Facts (History, Stats,…). Gamesver. 2022-05-10 [2022-07-23]. （原始内容存档于2022-07-23） （英语）.
- ^ 10.0 10.1 Edwards, Benj. Every Game Microsoft Ever Included in Windows, Ranked. How-To Geek. 2022-07-18 [2022-08-02]. （原始内容存档于2022-10-15） （英语）.
- ^ Scullion, Chris. News: Pokémon HeartGold/SoulSilver mini-game revealed! - Official Nintendo Magazine. officialnintendomagazine.co.uk. 2010-02-03 [2020-01-13]. （原始内容存档于2010-02-06） （英语）.
- ^ Shinkle, Ky. Every Minecraft April Fools Joke (Including 2022). Screen Rant. 2022-05-07 [2022-07-23]. （原始内容存档于2022-07-23） （英语）.
- ^ HP 48 Miscellaneous Games. www.hpcalc.org. [2022-07-23]. （原始内容存档于2022-07-13） （英语）.
- ^ Sidhwani, Priyansh. How To Play Google Minesweeper. TechStory. 2022-10-06 [2022-12-13]. （原始内容存档于2022-12-13） （美国英语）.
- ^ Minesweeper Puzzles Magazine. www.puzzle-magazine.com. [2022-07-24]. （原始内容存档于2022-08-28） （英语）.
- ^ Fastest combined completion time of Minesweeper. Guinness World Records. [2025-02-02] （中文及英语）.
- ^ Dr Sadie Kaye MA PhD. birmingham.ac.uk. University of Birmingham. [2023-10-16] （英语）.
- ^ Kaye, Richard. Minesweeper is NP-complete!. Mathematical Intelligencer. March 2000, 22 (2): 9–15 [2004-08-20]. ISSN 1866-7414. S2CID 122435790. doi:10.1007/BF03025367. （原始内容存档于2004-08-15） （英语）.
- ^ Scott, Allan; Stege, Ulrike; van Rooij, Iris. Minesweeper May Not Be NP-Complete but Is Hard Nonetheless. The Mathematical Intelligencer. December 2011, 33 (4): 5–17. S2CID 122506352. doi:10.1007/s00283-011-9256-x （英语）.
- ^ Dempsey, Ross; Guinn, Charles. A Phase Transition in Minesweeper. 2020. arXiv:2008.04116
[cs.AI] （英语）.
- ^ Kaye, Richard. Infinite versions of minesweeper are Turing complete (PDF). 2007-05-31 [2016-07-08]. （原始内容 (PDF)存档于2016-08-03） （英语）.
来源
[编辑]- Adamatzky, Andrew. How cellular automaton plays Minesweeper. Applied Mathematics and Computation. 1997, 85 (2–3): 127–137. doi:10.1016/S0096-3003(96)00117-8 （英语）.
- Lakshtanov, Evgeny; Oleg German. 'Minesweeper' and spectrum of discrete Laplacians. Applicable Analysis. 2010, 89 (12): 1907–1916. S2CID 17474183. arXiv:0806.3480 . doi:10.1080/00036811.2010.505189 （英语）.
- Mordechai Ben-Ari. Minesweeper is NP-Complete (PDF) (报告). Weizmann Institute of Science, Department of Science Teaching. 2018. （原始内容 (PDF)存档于2019-06-09） （英语）.