相干态是量子力学中量子諧振子能够达到的一种特殊的量子状态[1]。量子諧振子的动力学性能和经典力学中的諧振子很相似。1926年埃尔温·薛定谔在解满足对应原理的薛定谔方程时找到的第一个量子力学解就是相干态[2]。量子諧振子和相干态存在于大量物理系统中,比如一个位于二次方位能井中的粒子的振荡运动就是一个相干态。1963年罗伊·格劳伯把相干态引入量子電動力學和玻色子量子场论。
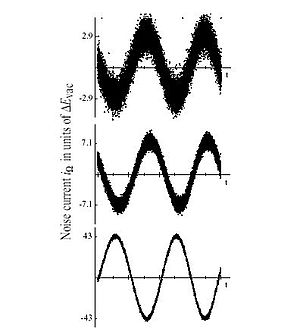 图1:使用零差检波测量的Nd:YAG激光器发射的电场的三种不同的相干态与相之间的函数关系,电场中量子噪音的数量与相完全不相关。量子噪音不随场强度的增高(振幅)而增强,因此变得越来越不足道。在强度非常高的情况下振荡就好像是完全没有噪音的经典波一样。从上向下平均光子数位4.2、25.2和924.5
图1:使用零差检波测量的Nd:YAG激光器发射的电场的三种不同的相干态与相之间的函数关系,电场中量子噪音的数量与相完全不相关。量子噪音不随场强度的增高(振幅)而增强,因此变得越来越不足道。在强度非常高的情况下振荡就好像是完全没有噪音的经典波一样。从上向下平均光子数位4.2、25.2和924.5
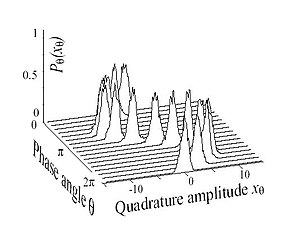 图2:图1中第二相干态的振荡波包。不论电场的相是多少其分布是宽度不变的高斯分布
图2:图1中第二相干态的振荡波包。不论电场的相是多少其分布是宽度不变的高斯分布
 图3:图2的相干态的維格納分佈分布的中心是相干态的振幅,而且是从这一点出发完全对称的。图中的波动是由试验误差导致的
图3:图2的相干态的維格納分佈分布的中心是相干态的振幅,而且是从这一点出发完全对称的。图中的波动是由试验误差导致的
相干态是最小不确定态,其唯一的一个自由系数可选为使得其位置和动量的相对弥散相等,在高能下这两个弥散均非常小。此外因为在所有能量特徵态中海森堡运动公式的期望值为零,相干态的期望值与经典运动公式完全相等,在高能量时其弥散非常小。
虽然最小不确定高斯式波包是众所周知的,但是直到1963年格劳伯提出完全量子化的电磁场理论才受到注意[3]。
在经典光学裡光被看作光源散发出来的电磁波。相干激光一般被看作是许多等相光源发出的光。但是在量子理论中一个光子和另一个光子等相这个说法不成立。激光辐射是由共振频率与为该电磁场提供能量的原子跃迁的频率相同的空间造成的。随着共振谐振模不断增强只有在这一个模产生受激的可能性提高。这是一个正反馈,谐振模的波幅不断提高,最后一个非线性效应限制它继续无限提高。作为一个反例子,电灯泡辐射的光的模是连续的,没有任何效应特别优惠一个模。辐射过程在时间和地点上非常偶然。在激光裡光只在谐振模上辐射,这个模因此非常相干。因此激光可以被理想化为相干态。
线性量子谐振子的能量特征态是定量量子态。相干态的量子力学互补坐标(位置和动量)的不确定相等,相和波幅的不确定约相等,而且在波幅高的情况下非常小。
相干态 被定义为湮没算符
被定义为湮没算符 的本征态:
的本征态:

由于 不是自伴算子,通常来说,本征值
不是自伴算子,通常来说,本征值 是一个复数,它可以被表示为
是一个复数,它可以被表示为

这裡 是一个实数。
是一个实数。 和
和 分别被称为是相干态的振幅和相。
分别被称为是相干态的振幅和相。
这个公式的物理意义是粒子的测量或者湮灭对相干态不造成变化,使用能量本征态为基表示出湮灭算符的本征态时其归一化系数具有泊松分布的形式。这是从统计观点上来看所有测量相互独立的充分必要条件。与单粒子态( Fock态)相比:在单粒子状态下假如我们测量到一个粒子的话再测量到另一个的可能性就降低到了零。
Fock态)相比:在单粒子状态下假如我们测量到一个粒子的话再测量到另一个的可能性就降低到了零。
它可由无量纲因次算符X和P导出。这两个算符可以由一个质量为m,角频率为ω的线性谐振子的位置和动量表示:
 其中
其中
对于光场来说

和

是腔体V内电场模式的实部和虚部。
使用这两个(无量纲的)算符,系统的哈密顿量为
 其中
其中![{\displaystyle \left[\mathbf {X} ,\mathbf {P} \right]\equiv \mathbf {XP} -\mathbf {PX} =i/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ed254e3b7e562922852cba8a4ece7ccc290e09a)
埃尔温·薛定谔在寻找最接近经典物理的态的时候引入了最小不确定高斯分布波包。使得不确定相同地分布在X和P上的最小不确定性关系满足以下方程
 或
或
这是算符(P-iX)的一个特征值。
薛定谔发现线性和谐振荡器的最小不确定态是(X+iP)的特征值,格劳伯在使用多光子状态时发现电磁场所有状态完全相干态必须是湮沒算符的正确特征值——在公式上,从数学角度出发,是同一状态。从格劳伯的成就开始相干态这个概念建立了。
相干态在相空間的位置的中心是同样相θ和振幅的经典振荡器的位置和动量。不确定性向所有方向同性扩展,由直径为1/2的圆盘表示。随着相的增高相干态环绕原点盘旋,但是圆盘即不变形也不扩大。这是一个量子状态在相空间中能够最接近一个点的状态。
如同图1所示,由于不确定始终是1/2而不随振荡子的振幅增高,这个状态越来越像一个正弦曲线。而且由于真空状态 也只不过是
也只不过是 的相干态,所有相干态的不确定和真空一样。因此相干态的真空噪声可以被看作是虛粒子的原因。
的相干态,所有相干态的不确定和真空一样。因此相干态的真空噪声可以被看作是虛粒子的原因。
特征值公式的解相当于把真空状态移动到相空间中的 ,既对真空使用位移算符
,既对真空使用位移算符 :
:

把相干态的公式用在单光子基础上:

这裡 是哈密尔顿方程的能量特征值。这是一个泊松分布。测量到
是哈密尔顿方程的能量特征值。这是一个泊松分布。测量到 光子的可能性为:
光子的可能性为:

类似的,相干态的平均光子数为 ,其方差为
,其方差为 。
。
 图4:测量到n光子的可能性,图3相干态的光子数分布。由于泊松分布的需要平均分子数等于分子数分布的方差。方块表示理论值,圆点是试验数据
图4:测量到n光子的可能性,图3相干态的光子数分布。由于泊松分布的需要平均分子数等于分子数分布的方差。方块表示理论值,圆点是试验数据
在 非常大的极限情况下这个测量统计与经典稳定波一样。这个结果适用于使用单一测量器测量的结果,因此适用于一度相干。但是要计算多个测量器的测量结果的话需要使用高度相干。格劳伯的量子相干态定义包含n度相干函数。完美的相干态含有所有n度相干等于1。
非常大的极限情况下这个测量统计与经典稳定波一样。这个结果适用于使用单一测量器测量的结果,因此适用于一度相干。但是要计算多个测量器的测量结果的话需要使用高度相干。格劳伯的量子相干态定义包含n度相干函数。完美的相干态含有所有n度相干等于1。
在 的情况下
的情况下 。由此可以看出数量不确定和相不确定之间有点互补的联系
。由此可以看出数量不确定和相不确定之间有点互补的联系 ,不过这个联系并不是正式的,量子力学中没有特别的相算符[4][5]。
,不过这个联系并不是正式的,量子力学中没有特别的相算符[4][5]。
两个不同的相干态不垂直:

所以

因此只有 時,兩個相干態才會近似正交。但由于它们之间有完备性关系,任何状态可以被分解为一系列相干态。这个完备性关系也可以这样来表达:
時,兩個相干態才會近似正交。但由于它们之间有完备性关系,任何状态可以被分解为一系列相干态。这个完备性关系也可以这样来表达:

為了證明上式,只要證明對任意兩個態 和
和 皆滿足
皆滿足

另外,算符 並不存在本徵右矢,而算符
並不存在本徵右矢,而算符 並不存在本徵左矢,以下公式在计算中很有用:
並不存在本徵左矢,以下公式在计算中很有用:

使用相干態來代表氦4的組成部分可以很好地體現出超液態裡凝聚和非凝聚之間的比例,其結果與慢中子散射的測量結果一致。使用一個相干態來表示超液態組成部分可以直接推導出大多數超液的特殊特性,這個相干態在整個超液體積裡擁有相同的波幅和相。
在研究超流體的初期羅傑·彭羅斯和拉斯·昂薩格[6]建議使用一個一級約化密度矩陣的宏觀係數項(一個宏觀特徵值)作為超流體的參數。後來楊振寧[7]提議了一個更廣義的宏觀量子相干態的參數,這個新參數即可以用於玻色子也可以用於費米子。它適用於任何級的約化密度矩陣。超流體是一級的,超導體是二級的。
描寫宏觀量子相干態使用的約化密度矩陣中的級在公式上和描寫輻射相干態的相干函數一樣。兩者都是宏觀量子相干態。格勞伯描寫的信號加噪聲所導致的電磁場中的相干態成分加上噪聲與超流體裡超流體部分和一般流體部分的描寫是一樣的。
电子是费米子,但是它们成对形成庫柏對后像玻色子一样反应,能够在低温下一起形成相干态。
在量子场论和弦理论中相干态被广义扩展到无限多自由度来定义与原真空的真空期望值不同的真空状态。
在一维费米子自由度的多体量子系统中低能激发态可以用玻色子场算符来近似表示,这个近似被称为玻色子化。
高斯分布的非相对论量子力学相干态可以被广义扩展为相对论相干态。
- ^ J.R. Klauder和B. Skagerstam《Coherent States》,World Scientific Publishing Co. Pte. Ltd.,新加坡,1985年
- ^ E. Schrödinger,《Naturwissenschaften》,14卷(1926年)664页
- ^ R.J. Glauber《Phys. Rev.》131卷(1963年)2766页
- ^ Susskind和Glowgower《Phys. Letters》(1963年)
- ^ Carruthers和Nieto《Rev. Mod. Phys.》(1968年)
- ^ Phys. Rev. 104, 576 (1956)
- ^ C. N. Yang, Rev. Mod Phys. 34, 694 (1962)



















![{\displaystyle \left[\mathbf {X} ,\mathbf {P} \right]\equiv \mathbf {XP} -\mathbf {PX} =i/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ed254e3b7e562922852cba8a4ece7ccc290e09a)


























