(a)

對最初100個質數的值
(b)

對最初200個質數的值
(c)

對最初500個質數的值
安德里卡猜想對最初(a)100個、(b)200個和(c)500個質數的圖像化證明。猜想的內容指稱,

總小於一。
安德里卡猜想(Andrica's conjecture)是關於質數間的間隙的猜想[1],以罗马尼亚数学家多林·安德里卡的名字命名。
該猜想認為,對於任意的 ,下述不等式成立:
,下述不等式成立:

其中 是第
是第 個質數。若
個質數。若 是第
是第 個質數間隙,那麼安德里卡猜想可表述如下:
個質數間隙,那麼安德里卡猜想可表述如下:

伊姆兰·戈里(Imran Ghory)用了大質數間隙的資料,證實了該猜想對大到 的
的 都成立。[2]利用最大質數間隙(maximal gap)和質數間隙不等式,可將此結果推廣到大到
都成立。[2]利用最大質數間隙(maximal gap)和質數間隙不等式,可將此結果推廣到大到 的
的 之上。
之上。
離散方城 呈遞減,其中
呈遞減,其中 的「高水位」標記,出現在
的「高水位」標記,出現在 之處,其中
之處,其中 ,而對於最初的
,而對於最初的 個質數而言,沒有比這更大的值。由於
個質數而言,沒有比這更大的值。由於 該方程對
該方程對 呈現非病態遞減之故,因此若要在
呈現非病態遞減之故,因此若要在 不斷變大的情況下使得這個差變大,一個不斷增長的質數間隙是必要的。故該猜想非常可能是正確的,但目前還沒有證明。
不斷變大的情況下使得這個差變大,一個不斷增長的質數間隙是必要的。故該猜想非常可能是正確的,但目前還沒有證明。
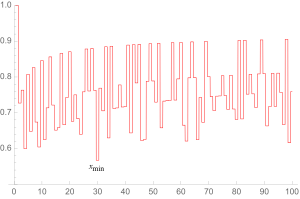 廣義安德里卡猜想對最初100個質數的x的值,並標出x的最小可能解
廣義安德里卡猜想對最初100個質數的x的值,並標出x的最小可能解 的推測位置。
的推測位置。
安德里卡猜想的推廣會論及以下等式:

其中 是第
是第 個質數,而x是任意正實數。
個質數,而x是任意正實數。
易證x的最大可能解出現於 處,在此處,
處,在此處, ;而有猜想認為,x的最小可能解出現於
;而有猜想認為,x的最小可能解出現於 處,在此處,
處,在此處, 。(OEIS數列A038458)
。(OEIS數列A038458)
該猜想也可以不等式表述,因此廣義安德里卡猜想可表述如下:
- 對於
 而言,
而言,
- ^ Andrica, D. Note on a conjecture in prime number theory. Studia Univ. Babes–Bolyai Math. 1986, 31 (4): 44–48. ISSN 0252-1938. Zbl 0623.10030.
- ^ Prime Numbers: The Most Mysterious Figures in Math, John Wiley & Sons, Inc., 2005, p. 13.
























