内维尔Θ函數(Neville Theta functions)共有四个,定义如下:





其中



尼维尔Θ函数也可以通过雅可比Θ函数的傅里叶级数来定义,并使得尼维尔Θ函数可以进一步被用于定义相对应的雅可比椭圆函数。




这种定义涉及到第一类完全椭圆积分。
利用Maple,将z=2.5,m=3 代人上列公式,即得: 与wolfram math结果相当[1]
:












![{\displaystyle NevilleThetaC(z,m)={\sqrt {2}}{\sqrt {\pi }}{\sqrt[{4}]{{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}}\sum _{k=0}^{\infty }\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{k\left(k+1\right)}\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right){{\rm {M}}\left(1,\,2,\,2\,i\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)\right)}\left({{\rm {e}}^{i\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)}}\right)^{-1}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}{\frac {1}{\sqrt[{4}]{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a41fca93eb297b5ce98334c3e1a295fed4cc3d62)

![{\displaystyle NevilleThetaN(z,m)=1/2\,{\sqrt {2}}{\sqrt {\pi }}\left(1+2\,\sum _{k=1}^{\infty }\left(-1\right)^{k}\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{{k}^{2}}\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right){{\rm {M}}\left(1,\,2,\,2\,i\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)\right)}\left({{\rm {e}}^{i\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)}}\right)^{-1}\right){\frac {1}{\sqrt[{4}]{1-m}}}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0c3d45ccf4eed42fcac01b5a00ba0cbe98c4baa)
![{\displaystyle NevilleThetaS(z,m)={\sqrt {2}}{\sqrt {\pi }}{\sqrt[{4}]{{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}}\sum _{k=0}^{\infty }1/2\,\left(-1\right)^{k}\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{k\left(k+1\right)}\left(2\,k+1\right)\pi \,z{{\rm {M}}\left(1,\,2,\,{\frac {i\pi \,z\left(2\,k+1\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}\right)}\left({\it {EllipticK}}\left({\sqrt {m}}\right)\right)^{-1}\left({{\rm {e}}^{\frac {1/2\,i\pi \,z\left(2\,k+1\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}\right)^{-1}{\frac {1}{\sqrt[{4}]{1-m}}}{\frac {1}{\sqrt[{4}]{m}}}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/034646b9b7bf8483712fc3347b82228097fe004f)
 Neville ThetaC function Maple plot Neville ThetaC function Maple plot
|
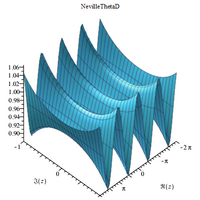
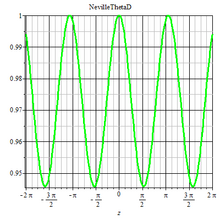 Neville ThetaD function Maple plot Neville ThetaD function Maple plot
|
 Neville ThetaD function Maple plot Neville ThetaD function Maple plot
|
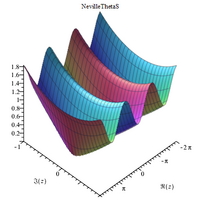
 Neville ThetaS function Maple plot Neville ThetaS function Maple plot
|
- Milton Abramowitz and Irene Stegun,Handbook of Mathematical Functions, p578, National Bureau of Standards, 1972.
- ^ wolfram math 计算结果. [2015-03-09]. (原始内容存档于2020-06-14).































![{\displaystyle NevilleThetaC(z,m)={\sqrt {2}}{\sqrt {\pi }}{\sqrt[{4}]{{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}}\sum _{k=0}^{\infty }\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{k\left(k+1\right)}\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right){{\rm {M}}\left(1,\,2,\,2\,i\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)\right)}\left({{\rm {e}}^{i\left(1/2\,{\frac {\left(2\,k+1\right)\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)}}\right)^{-1}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}{\frac {1}{\sqrt[{4}]{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a41fca93eb297b5ce98334c3e1a295fed4cc3d62)

![{\displaystyle NevilleThetaN(z,m)=1/2\,{\sqrt {2}}{\sqrt {\pi }}\left(1+2\,\sum _{k=1}^{\infty }\left(-1\right)^{k}\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{{k}^{2}}\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right){{\rm {M}}\left(1,\,2,\,2\,i\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)\right)}\left({{\rm {e}}^{i\left({\frac {k\pi \,z}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}+1/2\,\pi \right)}}\right)^{-1}\right){\frac {1}{\sqrt[{4}]{1-m}}}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0c3d45ccf4eed42fcac01b5a00ba0cbe98c4baa)
![{\displaystyle NevilleThetaS(z,m)={\sqrt {2}}{\sqrt {\pi }}{\sqrt[{4}]{{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}}\sum _{k=0}^{\infty }1/2\,\left(-1\right)^{k}\left({{\rm {e}}^{-{\frac {\pi \,{\it {EllipticK}}\left({\sqrt {1-m}}\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}\right)^{k\left(k+1\right)}\left(2\,k+1\right)\pi \,z{{\rm {M}}\left(1,\,2,\,{\frac {i\pi \,z\left(2\,k+1\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}\right)}\left({\it {EllipticK}}\left({\sqrt {m}}\right)\right)^{-1}\left({{\rm {e}}^{\frac {1/2\,i\pi \,z\left(2\,k+1\right)}{{\it {EllipticK}}\left({\sqrt {m}}\right)}}}\right)^{-1}{\frac {1}{\sqrt[{4}]{1-m}}}{\frac {1}{\sqrt[{4}]{m}}}{\frac {1}{\sqrt {{\it {EllipticK}}\left({\sqrt {m}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/034646b9b7bf8483712fc3347b82228097fe004f)