貝爾數(英語:Bell number)是組合數學中的一組整數數列,以埃里克·坦普尔·贝尔命名,首幾個貝爾數為:
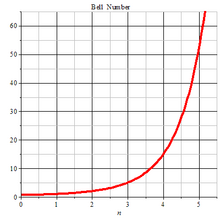 Bell Number
Bell Number
 (OEIS數列A000110)
(OEIS數列A000110)
 是基數為
是基數為 的集合的劃分方法的數目。集合
的集合的劃分方法的數目。集合 的劃分是
的劃分是 的兩兩不相交的非空子集的族,它們的並是
的兩兩不相交的非空子集的族,它們的並是 。例如,
。例如, ,因為有3個元素的集合
,因為有3個元素的集合 有5種不同的劃分方法:
。
有5種不同的劃分方法:
。




 ;
;
 因為空集正好有1種劃分方法。空集的每個成員都是非空集合(这是Vacuous truth,因为空集实际上没有成員),而它們的並是空集本身。所以空集是它的唯一劃分。
因為空集正好有1種劃分方法。空集的每個成員都是非空集合(这是Vacuous truth,因为空集实际上没有成員),而它們的並是空集本身。所以空集是它的唯一劃分。
貝爾數滿足遞推公式:

上述组合公式的证明:
可以这样来想, 是含有n+1个元素集合的划分的个数,考虑元素
是含有n+1个元素集合的划分的个数,考虑元素
假设他被单独划分到一类,那么还剩下n个元素,这种情况下划分个数为 ;
;
假设他和某一个元素被划分为一类,那么还剩下n-1个元素,这种情况下划分个数为  ;
;
假设他和某两个元素被划分为一类,那么还剩下n-2个元素,这种情况下划分个数为  ;
;
依次类推,得到了上述组合公式
它們也適合「Dobinski公式」:
 期望值為1的泊松分數的n次矩。
期望值為1的泊松分數的n次矩。
它們也適合「Touchard同餘」:若p是任意質數,那麼

每個貝爾數都是"第二類Stirling數"的和

Stirling數S(n, k)是把基數為n的集劃分為正好k個非空集的方法的數目。
把任一概率分佈的n次矩以首n個累積量表示的多項式,其係數和正是第n個貝爾數。這種數劃分的方法不像用Stirling數那個方法粗糙。
貝爾數的指數母函數是

用以下方法建構一個三角矩陣(形式類似楊輝三角形):
- 第一行第一項是1(
 )
)
- 對於n>1,第n行第一項等同第n-1行最後一項。(
 )
)
- 對於m,n>1,第n行第m項等於它左邊和左上方的兩個數之和。(
 )
)
結果如下:(OEIS:A011971)

每行首項是貝爾數。每行之和是第二類Stirling數。
這個三角形稱為貝爾三角形、Aitken陣列或Peirce三角形(Bell triangle, Aitken's array, Peirce triangle)。


























