着色

在電腦圖學中,著色,也称浓淡处理、明暗处理、着色法(英語:Shading)是在三维模型或插画中通过不同的亮度表现深度的方法。
绘图
[编辑]
浓淡处理是用较大压力在纸上绘制较深颜色、用较小压力绘制较浅颜色从而表示不同明暗程度的过程。有许多不同的浓淡处理技术,其中交叉影线是用不同距离互相垂直的网格线绘制不同区域的浓淡。影线距离越近,所绘制区域越暗;相反,距离越远,所绘制区域越亮。这个术语近来用来泛指使用浓淡工具的场合。
物体都有照亮区域以及阴影区域这样不同的光照模式,这种现象可以用于在纸上以及计算机屏幕上显示不同的深度。
计算机图形学
[编辑]在计算机图形学中,浓淡处理表示根据物体相对于光线的角度及其与光源的距离改变物体明暗生成photorealistic效果的过程。浓淡处理是在渲染过程中的一步,由着色器完成。
光照模型
[编辑]浓淡处理的算法因光源种类而异。 通常来说多种效果会在一起使用,以增加场真实性。因为不同类型的光源会效果不一。
环境光
[编辑]环境光光源是一个固定强度,固定颜色的光源,他无方向无差别地作用于所有物体。所有物体都会有一样的颜色和亮度。这样的光源主要用于提供一个基本照明。这是最简单的一种照明模型,也能模拟光线被多次反射散射后产生的一个均一的效果。
有向光
[编辑]有向光从一个方向无差别地照亮所有物体。就像一个无限大和无限远的区域光源。他会在物体表面产生明暗效果, 但不会根据距离衰减。
点光
[编辑]光从一点出发,向所有方向投射。
聚光灯光
[编辑]模拟一个聚光灯。 光从锥形顶点向底部投射。
区域光
[编辑]光从平面上的一小区域发出,是比点光源更准确的模型。
有体积光
[编辑]光从一个有体积的小物体发出。
相对于光源的角度
[编辑]除了环境光以外,其他光都是有方向性的。根据物体表面和光线的夹角不同,浓淡处理算法会改变三维模型中的表面颜色和明暗程度。
下面的第一张图中的盒子的每个表面都用同一种颜色进行渲染,画出边线是为了易于观看。
第二张图是同一张模型,但是没有绘制边线。我们很难分辨出这张图的每一个表面。
第三种进行了浓淡处理,这样图像看起来更加真实,也易于分辨每个表面。
距离衰减
[编辑]理论上讲,如太阳这样的远距离光源对于两个平行表面的的照明亮度是一样的,尽管其中一个表面可能较远,但亮度仍然看起来是一样的。
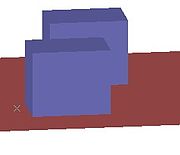
注意在第一幅图中,两个盒子正面的颜色是完全相同的。但是在两个表面相交的地方看起来颜色有些差别,这是因为在两个表面相交部分下面还有一段竖直边缘带来的视觉幻觉。
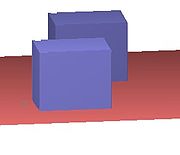
在第二幅图中,前面盒子的正面比后面盒子的正面要亮,并且地板也从前到后逐渐变暗。
这种 距离衰减 效果生成的图像看起来更加真实,并且不需要添加额外的照明来实现同样的效果。
-
使用OpenGL渲染工具生成的两个盒子
-
用ARRIS CAD渲染的同一模型,它实现了“Distance Falloff”从而距离较近的表面看起来更加明亮
距离衰减的计算可以有以下几种算法
- 无 - 光强跟点于光源之间的距离无关。
- 线性 - 光强正比于距离的倒数。
- 二次 - 光强正比于距离倒数的平方。这是在无雾或其他东西吸收或者散射的情况下光强的真实衰减模型。
- n阶 - 光强正比于距离倒数的n次方。
- 其他计算方式也可以
插值技术
[编辑]
渲染过程中需要计算表面的亮度,上述光照模型要求我们提前知道表面上任意点的法线。然而,三维模型一般都是通过多边形网格描述的,只能在有限的点存储法线,这些点通常是多边形的顶点。为了解决这一问题,可以使用不同的插值技术。
平直着色法
[编辑]平直着色法(英語:flat shading)基于「组成模型的多边形都是平的」的假设,认为在同一多边形上任意点的法线都相同。
使用这种着色法时,先在每个多边形上挑选一个点计算颜色(通常是多边形的第一个顶点,如果是三角形网格则也可以选择几何中心),则该多边形上其余点都直接使用该点的颜色。所以,使用平直着色法的每个多边形上都是统一的颜色,和最近邻插值的效果类似。
其它更加高级的着色技术由于计算量太大不便于使用时,这种方法经常用于高速渲染。由于每个多边形都是统一的颜色,所以使用这种着色法也更易于区分相邻的多边形。但这种着色法很难做出高光效果:一个表面要不全高光,要不全没有,因此高光模型很少使用在这个着色方法中。
平滑着色法
[编辑]使用平直着色法时,颜色在多边形的边缘跳变。而使用平滑着色法(英語:smooth shading)时,每个像素的颜色都可以不同,相邻多边形之间的颜色转变看上去就比较平滑。通常先计算多边形顶点的颜色,再通过双线性插值来确定多边形上其它点的像素值。
常见的平滑着色包括:
- Gouraud着色法 [3]
- Phong着色法 [4]
此外,还有通过泰勒级数展开[1]、球面线性插值[2]等方法实现的平滑着色法。
Gouraud着色法
[编辑]- 计算多边形的顶点法向量
- 用光照模型去计算每个顶点的光强
- 用双线性插值计算多边形表面上每个像素的明暗
有时顶点法向量能被直接计算(如均一网格上的高度图)。更一般来说我们需要一个有效的数据结构,能快速找到哪些多边形共用这个顶点。
Gouraud着色法的优势在于,即便是比三角形复杂的多边形,每个顶点也可以有不一样的颜色,内部插值算法可以更多变。
而Gouraud着色法也有一些问题:
- 邻接多边形可能有不一样的颜色。
- Gouraud着色 需要比较大的CPU计算量,在实时处理大量多边形时可能会成为问题。
- 3个多边形边的T型连接可能会被错误的绘制,一般来说应该避免存在T型连接
Phong着色法
[编辑]Phong着色法与Gouraud着色法类似,区别在于进行双线性插值的不是光照强度本身,而是顶点的法线。因此使用这种着色法计算出的高光比Gouraud着色更精确。
- 计算多边形顶点的法向量
- 双线性插值计算每个像素点的法向量
- 通过每个像素的法向量计算光强
- 根据光强绘制像素
平直着色与平滑着色对比
[编辑]| 平直着色 | 平滑着色 |
|---|---|
| 一个面的所有像素用同一种颜色,一般是第一个顶点的颜色 | 对顶点的颜色进行插值运算,每个像素不一样 |
| 边比真實物体更明显lateral inhibition | 边看不见 |
| 绘制出每个平面 | 绘制出光滑曲面 |
| 不适合光滑物体 | 适合光滑物体 |
| 计算量少 | 计算量大 |