拉東變換將函數
f
(
x
,
y
)
{\displaystyle f(x,y)}
f
(
α
,
s
)
{\displaystyle f(\alpha ,s)}
本圖是將下圖做拉東變換後得到的影像,越亮的區域代表值越大,黑色的區域為0。 原始函數是白色區域為1,黑色區域為0。 數學 上,拉東變換 (又稱雷登變換 )是一種積分變換 ,這個變換將二維平面函數
f
{\displaystyle f}
R
f
{\displaystyle {\cal {R}}f}
R
f
{\displaystyle {\cal {R}}f}
f
{\displaystyle f}
R
f
{\displaystyle {\cal {R}}f}
f
{\displaystyle f}
R
f
{\displaystyle {\cal {R}}f}
f
{\displaystyle f}
A
{\displaystyle A}
R
f
{\displaystyle {\cal {R}}f}
拉東變換是约翰·拉东 在西元1917年提出[ 1] X射线变换 歐幾里得空間 的拉東變換被提出,更詳盡的廣義拉東變換要参见Integral geometry 複數 上有和拉東變換相似的Penrose变换 斷層掃描 ,拉東反變換可以從斷層掃描的剖面圖重建出投影前的函數。
若函數
f
{\displaystyle f}
f
{\displaystyle f}
f
{\displaystyle f}
f
{\displaystyle f}
f
{\displaystyle f}
三維重建 。
拉東變換後的訊號稱作正弦圖 (sinogram ),因為一個偏離中心的點的拉東變換是一條正弦曲線 。所以對一些小點的拉東變換,會看起來像很多不同振福、相位的正弦函數 重疊在一起。
拉東變換可以應用在:X射線電腦斷層掃描 、條碼 掃描器、大分子装配 電子顯微鏡 (例如:病毒 、蛋白質複合體 )、反射地震学 ,而且也是雙曲線偏微分方程 的解。
令密度函數
f
(
x
)
=
f
(
x
,
y
)
{\displaystyle f({\bf {x}})=f(x,y)}
R
2
{\displaystyle {\bf {R}}^{2}}
緊支撐 。令
R
{\displaystyle {\cal {R}}}
R
f
(
x
,
y
)
{\displaystyle {\cal {R}}f(x,y)}
R
2
{\displaystyle {\bf {R}}^{2}}
L
{\displaystyle L}
R
f
(
L
)
=
∫
L
f
(
x
)
|
d
x
|
{\displaystyle {\cal {R}}f(L)=\int _{L}f({\bf {x}})|d{\bf {x}}|}
可以把直線
L
{\displaystyle L}
z
{\displaystyle z}
(
x
(
z
)
,
y
(
z
)
)
=
(
(
z
sin
α
+
s
cos
α
)
,
(
−
z
cos
α
+
s
sin
α
)
)
{\displaystyle (x(z),y(z))={\Big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\Big )}\,}
s
{\displaystyle s}
L
{\displaystyle L}
α
{\displaystyle \alpha }
L
{\displaystyle L}
x
{\displaystyle x}
(
α
,
s
)
{\displaystyle (\alpha ,s)}
R
2
{\displaystyle {\bf {R}}^{2}}
R
f
(
α
,
s
)
=
∫
−
∞
∞
f
(
x
(
z
)
,
y
(
z
)
)
d
z
=
∫
−
∞
∞
f
(
(
z
sin
α
+
s
cos
α
)
,
(
−
z
cos
α
+
s
sin
α
)
)
d
z
{\displaystyle {\begin{aligned}{\cal {R}}f(\alpha ,s)&=\int _{-\infty }^{\infty }f(x(z),y(z))\,dz\\&=\int _{-\infty }^{\infty }f{\big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\big )}\,dz\end{aligned}}}
更進一步,我們可以把
R
2
{\displaystyle {\bf {R}}^{2}}
R
n
{\displaystyle {\bf {R}}^{n}}
歐幾里得空間 ,對一個緊支撐 的連續函數
f
{\displaystyle f}
R
f
{\displaystyle {\cal {R}}f}
Σ
n
{\displaystyle \Sigma _{n}}
超平面 上,
R
f
(
ξ
)
=
∫
ξ
f
(
x
)
d
σ
(
x
)
,
f
o
r
ξ
∈
Σ
n
{\displaystyle {\cal {R}}f(\xi )=\int _{\xi }f(\mathbf {x} )\,d\sigma (\mathbf {x} ),\quad {\rm {for}}\quad \xi \in \Sigma _{n}}
積分的對象是自然超平面測度(natural hypersurface measure),而
d
Δ
{\displaystyle d\Delta }
|
d
x
|
{\displaystyle |d{\bf {x}}|}
Σ
n
{\displaystyle \Sigma _{n}}
x
⋅
α
=
s
.
{\displaystyle {\bf {x}}\cdot \alpha =s.}
而
α
{\displaystyle \alpha }
單位向量 且屬於
S
n
−
1
{\displaystyle {\rm {S}}^{n-1}}
s
∈
R
{\displaystyle s\in \mathbb {R} }
S
n
−
1
×
R
{\displaystyle {\rm {S}}^{n-1}\times {\bf {R}}}
R
f
(
α
,
s
)
=
∫
x
⋅
α
=
s
f
(
x
)
d
σ
(
x
)
{\displaystyle {\cal {R}}f(\alpha ,s)=\int _{\mathbf {x} \cdot \alpha =s}f(\mathbf {x} )\,d\sigma (\mathbf {x} )}
也可以藉由其他方式將拉東變換推廣,也就是對
R
n
{\displaystyle {\bf {R}}^{n}}
X射線電腦斷層掃描 ,他的做法是對一條直線積分。
拉東變換和傅立葉變換之間有很強的關聯性。單變數的傅立葉變換的定義是
f
^
(
ω
)
=
∫
−
∞
∞
f
(
x
)
e
−
2
π
i
x
ω
d
x
{\displaystyle {\hat {f}}(\omega )=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\omega }\,dx}
而雙變數
(
x
)
=
(
x
,
y
)
{\displaystyle ({\bf {x}})=(x,y)}
f
^
(
w
)
=
∫
−
∞
∞
∫
−
∞
∞
f
(
x
)
e
−
2
π
i
x
⋅
w
d
x
d
y
{\displaystyle {\hat {f}}(\mathbf {w} )=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(\mathbf {x} )e^{-2\pi i\mathbf {x} \cdot \mathbf {w} }\,dx\,dy}
把拉東變換的運算子的表記從
R
[
f
]
(
s
)
{\displaystyle {\cal {R}}[f](s)}
R
[
f
]
(
α
,
s
)
{\displaystyle {\cal {R}}[f](\alpha ,s)}
R
α
[
f
]
^
(
σ
)
=
f
^
(
σ
n
(
α
)
)
,
n
(
α
)
=
(
cos
α
,
sin
α
)
{\displaystyle {\widehat {{\mathcal {R}}_{\alpha }[f]}}(\sigma )={\hat {f}}(\sigma \mathbf {n} (\alpha )),\quad \mathbf {n} (\alpha )=(\cos \alpha ,\sin \alpha )}
因此一個初始函數沿著一條線傾角
α
{\displaystyle \alpha }
f
^
(
r
α
)
=
∫
−
∞
∞
R
f
(
α
,
s
)
e
−
2
π
i
s
r
d
s
{\displaystyle {\hat {f}}(r\alpha )=\int _{-\infty }^{\infty }{\mathcal {R}}f(\alpha ,s)e^{-2\pi isr}\,ds}
對偶拉東變換是拉東變換的埃爾米特伴隨 。令在空間
Σ
n
{\displaystyle \Sigma _{n}}
g
{\displaystyle g}
R
∗
{\displaystyle {\cal {R}}^{*}}
g
{\displaystyle g}
R
∗
g
(
x
)
=
∫
x
∈
ξ
g
(
ξ
)
d
μ
(
ξ
)
{\displaystyle {\mathcal {R}}^{*}g(x)=\int _{x\in \xi }g(\xi )\,d\mu (\xi )}
積分的範圍是所有和
x
∈
R
2
{\displaystyle x\in {\bf {R}}^{2}}
d
μ
{\displaystyle d\mu }
ξ
|
x
∈
ξ
{\displaystyle \xi |x\in \xi }
x
{\displaystyle x}
d
μ
{\displaystyle d\mu }
對於一個二維的拉東變換,其對偶變換是
R
∗
g
(
x
)
=
1
2
π
∫
α
=
0
2
π
g
(
α
,
n
(
α
)
⋅
x
)
d
α
{\displaystyle {\mathcal {R}}^{*}g(x)={\frac {1}{2\pi }}\int _{\alpha =0}^{2\pi }g(\alpha ,\mathbf {n} (\alpha )\cdot \mathbf {x} )\,d\alpha }
在影像處理的文章中,對偶變換經常被稱作反向投影(back-projection) [ 2]
交結性質
根據拉普拉斯算子
Δ
{\displaystyle \Delta }
R
n
{\displaystyle {\bf {R}}^{n}}
Δ
=
∂
2
∂
x
1
2
+
⋯
+
∂
2
∂
x
n
2
{\displaystyle \Delta ={\frac {\partial ^{2}}{\partial x_{1}^{2}}}+\cdots +{\frac {\partial ^{2}}{\partial x_{n}^{2}}}}
這是一個旋轉不變性 的二階微分算子 ,在空間
Σ
n
{\displaystyle \Sigma _{n}}
二階導數
L
f
(
α
,
s
)
≡
∂
2
∂
s
2
f
(
α
,
s
)
{\displaystyle Lf(\alpha ,s)\equiv {\frac {\partial ^{2}}{\partial s^{2}}}f(\alpha ,s)}
也是旋轉不變性 。
而拉東變換與其對偶變換屬於交結運算子(intertwining operator),是因為
R
(
Δ
f
)
=
L
(
R
f
)
,
R
∗
(
L
g
)
=
Δ
(
R
∗
g
)
{\displaystyle {\mathcal {R}}(\Delta f)=L({\mathcal {R}}f),\quad {\mathcal {R}}^{*}(Lg)=\Delta ({\mathcal {R}}^{*}g)}
重建處理 是指從投影影像重建一個影像,或是一個函數
f
{\displaystyle f}
逆問題 (inverse problem)。
拉東反變換公式
對於二維拉東變換,最常被使用的解析公式(analytical formula)
f
{\displaystyle f}
f
(
x
)
=
∫
0
π
(
R
f
(
⋅
,
θ
)
∗
h
)
(
⟨
x
,
n
θ
⟩
)
d
θ
{\displaystyle f(\mathbf {x} )=\int _{0}^{\pi }({\mathcal {R}}f(\cdot ,\theta )*h)(\left\langle \mathbf {x} ,\mathbf {n} _{\theta }\right\rangle )d\theta }
[ 3] 函數
h
{\displaystyle h}
h
^
(
k
)
=
|
k
|
{\displaystyle {\hat {h}}(k)=|k|}
[ 4]
h
{\displaystyle h}
不適定問題 (ill-posedness)
直覺上,反變換公式應該和微分類似,
d
d
x
^
f
(
x
)
=
i
k
f
^
(
k
)
{\displaystyle {\widehat {\frac {d}{dx}}}f(x)=ik{\hat {f}}(k)}
R
∗
R
g
^
(
k
)
=
1
|
|
k
|
|
g
^
(
k
)
{\displaystyle {\widehat {{\mathcal {R}}^{*}{\mathcal {R}}g}}(k)={\frac {1}{||\mathbf {k} ||}}{\hat {g}}(\mathbf {k} )}
R
∗
{\displaystyle {\cal {R}}^{*}}
g
(
x
)
=
e
i
⟨
k
0
,
x
⟩
{\displaystyle g({\bf {x}})=e^{i\langle {\bf {k}}_{0},{\bf {x}}\rangle }}
R
∗
R
g
=
1
|
|
k
|
|
e
i
⟨
k
0
,
x
⟩
{\displaystyle {\cal {R}}^{*}{\cal {R}}g={\frac {1}{||{\bf {k}}||}}e^{i\langle {\bf {k}}_{0},{\bf {x}}\rangle }}
複數指數函數
e
i
⟨
k
0
,
x
⟩
{\displaystyle e^{i\langle {\bf {k}}_{0},{\bf {x}}\rangle }}
R
∗
R
{\displaystyle {\cal {R}}^{*}{\cal {R}}}
固有函數 (eigenfunction) ,
而特徵值 (eigenvalue)為
1
|
|
k
|
|
{\displaystyle {\frac {1}{||{\bf {k}}||}}}
R
{\displaystyle {\cal {R}}}
1
|
|
k
|
|
{\displaystyle {\sqrt {\frac {1}{||{\bf {k}}||}}}}
R
−
1
{\displaystyle {\cal {R}}^{-1}}
[ 4]
外顯(explicit)且計算效率好的拉東反變換公式,以及他的對偶是存在的。n維的反拉東變換可以由[ 5]
c
n
f
=
(
−
Δ
)
(
n
−
1
)
/
2
R
∗
{
R
f
}
{\displaystyle c_{n}f=(-\Delta )^{(n-1)/2}{\cal {R}}^{*}\{{\cal {R}}f\}}
其中
c
n
=
(
4
π
)
(
n
−
1
)
/
2
Γ
(
n
/
2
)
Γ
(
1
/
2
)
{\displaystyle c_{n}=(4\pi )^{(n-1)/2}{\frac {\Gamma (n/2)}{\Gamma (1/2)}}}
而
Δ
{\displaystyle \Delta }
拉普拉斯算子 (Laplacian),
(
−
Δ
)
(
n
−
1
)
/
2
{\displaystyle (-\Delta )^{(n-1)/2}}
偽微分算子 (pseudodifferential operator)
F
[
(
−
Δ
)
(
n
−
1
)
/
2
ϕ
]
(
ξ
)
=
|
2
π
ξ
|
n
−
1
F
ϕ
(
ξ
)
.
{\displaystyle {\mathcal {F}}\left[(-\Delta )^{(n-1)/2}\phi \right](\xi )=|2\pi \xi |^{n-1}{\mathcal {F}}\phi (\xi ).}
F
{\displaystyle {\mathcal {F}}}
傅立葉變換 的運算子(operator)。
^ 存档副本 . [2017-06-29 ] . (原始内容存档 于2017-07-19). ^ Kak, Avinash C.; Slaney, Malcolm. Principles of Computerized Tomographic Imaging. Classics in applied mathematics. Philadelphia: Society for Industrial and Applied Mathematics. 2001. ISBN 978-0-89871-494-4 ^ 存档副本 (PDF) . [2017-06-29 ] . (原始内容 (PDF) 存档于2018-11-25). ^ 4.0 4.1 存档副本 (PDF) . [2017-06-29 ] . (原始内容 (PDF) 存档于2018-11-25). ^ Helgason 1984 ,Theorem I.2.13
Deans, Stanley R., The Radon Transform and Some of Its Applications, New York: John Wiley & Sons, 1983 Helgason, Sigurdur, Geometric analysis on symmetric spaces, Mathematical Surveys and Monographs 39 2nd, Providence, R.I.: American Mathematical Society , 2008, ISBN 978-0-8218-4530-1MR 2463854 Helgason, Sigurdur , Groups and Geometric Analysis: Integral Geometry, Invariant Differential Operators, and Spherical Functions, Academic Press, 1984, ISBN 0-12-338301-3 Herman, Gabor T. , Fundamentals of Computerized Tomography: Image Reconstruction from Projections 2nd, Springer, 2009, ISBN 978-1-85233-617-2 Minlos, R.A., Radon transform , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 Natterer, Frank, The Mathematics of Computerized Tomography, Classics in Applied Mathematics 32 , Society for Industrial and Applied Mathematics, ISBN 0-89871-493-1 Natterer, Frank; Wübbeling, Frank, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics, ISBN 0-89871-472-9 Radon, Johann , Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten, Berichte über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse [Reports on the proceedings of the Royal Saxonian Academy of Sciences at Leipzig, mathematical and physical section] (Leipzig: Teubner), 1917, (69): 262–277 Translation: Radon, J.; Parks, P.C. (translator), On the determination of functions from their integral values along certain manifolds, IEEE Transactions on Medical Imaging, 1986, 5 (4): 170–176, PMID 18244009 doi:10.1109/TMI.1986.4307775 Roerdink, J.B.T.M., Tomography , Hazewinkel, Michiel (编), 数学百科全书 , Springer , 2001, ISBN 978-1-55608-010-4 埃里克·韦斯坦因 . 拉東變換 . MathWorld . 

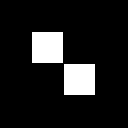
































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15f797153d26de6695006b53c3d5b374b62fe439)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca05f39a823774598e430ff88eecc89ddd009da8)
![{\displaystyle {\widehat {{\mathcal {R}}_{\alpha }[f]}}(\sigma )={\hat {f}}(\sigma \mathbf {n} (\alpha )),\quad \mathbf {n} (\alpha )=(\cos \alpha ,\sin \alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9b849ebddfdeaee53ee59098490ed5a830ea08)



























=|2\pi \xi |^{n-1}{\mathcal {F}}\phi (\xi ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74cd4b6777a1b180a2753a4e0267ba3f835854c)
